KindiakMath

Laplace Rally

Question 1. Evaluate \mathcal L\{1 - t^3 + e^{3t} + \sin(t)\}.

(Click for Solution)

Solution. By the linearity of Laplace transforms,

\begin{aligned} \mathcal L \{1 - t^3 + e^{3t} + \sin(t) \} &= \mathcal L \{ 1\} - \mathcal L \{ t^3 \} + \mathcal L \{ e^{3t} \} + \mathcal L \{ \sin(t) \} \\ &= \frac 1s - \frac{ 3! }{ s^{3+1} } + \frac 1{s-3} + \frac 1{s^2 + 1^2} \\ &= \frac 1s - \frac 6{s^4} + \frac 1{s-3} + \frac 1{s^2+1}. \end{aligned}

Question 2. Evaluate \displaystyle \mathcal L^{-1} \left\{ \frac 1{s^2} + \frac 1{s-2} + \frac 1{s^2+9} + \frac s{s^2+4} \right\}.

(Click for Solution)

Solution. By the linearity of inverse Laplace transforms,

\begin{aligned} & \mathcal L^{-1} \left\{ \frac 1{s^2} + \frac 1{s-2} + \frac 1{s^2+9} + \frac s{s^2+4} \right\}\\ &= \mathcal L^{-1} \left\{ \frac{1!}{s^{1+1}} \right\} + \mathcal L^{-1} \left\{ \frac 1{s-2} \right\} \\ &\phantom{==} + \frac 13 \cdot \mathcal L^{-1} \left\{ \frac 3{s^2 + 3^2} \right\} + \mathcal L^{-1} \left\{ \frac s{s^2 + 2^2} \right\} \\ &= t + e^{2t} + \frac 13 \sin(3t)+ \cos(2t). \end{aligned}

Question 3. The function f is defined by the graph below.

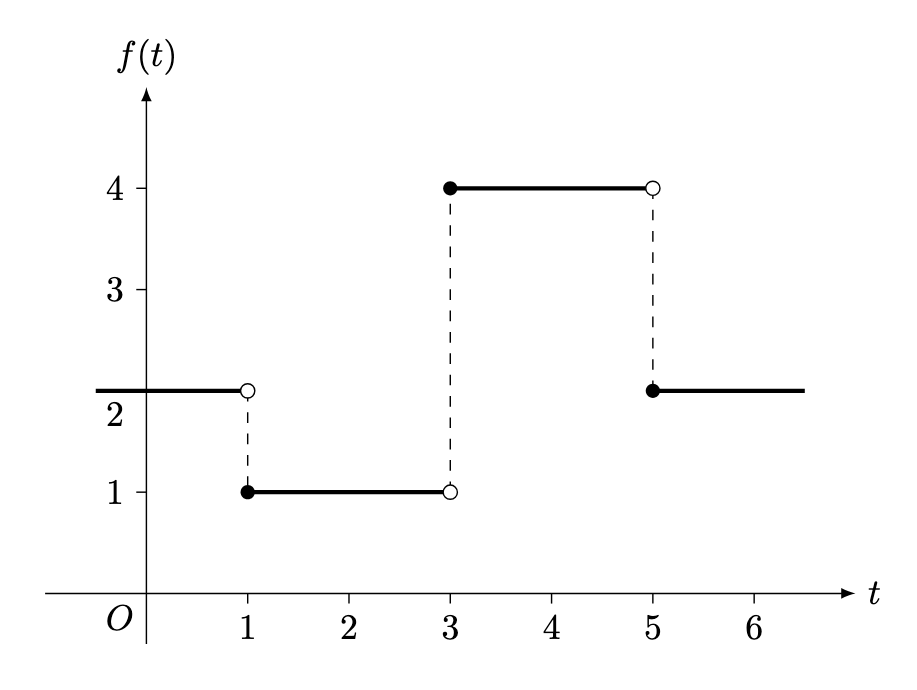
Evaluate \mathcal L\{e^t f(t)\} and \mathcal L\{f(t) U(t-2)\}.

(Click for Solution)

Solution. By observation,

f(t) = \begin{cases}2, &t < 1, \\ 1, & 1 \leq t < 3, \\ 4, & 3 \leq t < 5, \\ 2, & t \geq 5.\end{cases}

By the jump technique,

\begin{aligned} f(t) &= 2 + (1-2) \cdot U(t-1) + (4-1) \cdot U(t-3) + (2-4) \cdot U(t-5) \\ &= 2 - U(t-1) + 3 U(t-3) - 2 U(t-5). \end{aligned}

By the shift theorems, \mathcal L\{e^t f(t)\} = F(s-1).

Hence, we need to evaluate F(s) = \mathcal L\{f(t)\}:

\begin{aligned} F(s) &= \mathcal L\{f(t)\} \\ &= \mathcal L\{ 2 - U(t-1) + 3 U(t-3) - 2 U(t-5) \} \\ &= 2 \cdot \mathcal L\{ 1 \} - \mathcal L \{ U(t-1) \} + 3 \cdot \mathcal L\{ U(t-3) \} - 2 \cdot \mathcal L\{ U(t-5) \} \\ &= 2 \cdot \frac 1{s} - \frac{ e^{-s} }{s} + 3 \cdot \frac{ e^{-3s} }{s} - 2 \cdot \frac{ e^{-5s} }{s} \\ &= \frac 1s (2 - e^{-s} + 3 e^{-3s} - 2 e^{-5s}). \end{aligned}

Therefore,

\displaystyle \mathcal L\{e^t f(t)\} = F(s-1) = \frac 1{s-1} (2 - e^{-(s-1)} + 3 e^{-3(s-1)} - 2 e^{-5(s-1)}).

For the second result, we take advantage of the result

U(t - a) \cdot U(t - b) = U(t - \max\{a, b\})

to obtain f(t) \cdot U(t-2) = U(t-2) + 3 U(t-3) - 2 U(t-5). Taking Laplace transforms,

\begin{aligned} \mathcal L\{ f(t) \cdot U(t-2) \} &= \frac{e^{-2s}}{s} + 3 \cdot \frac{ e^{-3s} }{s} - 2\cdot \frac{ e^{-5s} }{s} \\ &= \frac 1s (e^{-2s} + 3e^{-3s} - 2e^{-5s}). \end{aligned}

Question 4. Evaluate \displaystyle \mathcal L^{-1} \left\{ \frac{4e^{-2s}}{s^2 + 2s + 2} \right\}.

(Click for Solution)

Solution. Motivated by the shift theorems, define F(s) = 4/(s^2+2s+2). Then

\begin{aligned} \mathcal L^{-1} \left\{ \frac{4e^{-2s}}{s^2 + 2s + 2} \right\} &= \mathcal L^{-1} \left\{ e^{-2s} F(s) \right\} = f(t-2) U(t-2). \end{aligned}

It remains to evaluate f(t) = \mathcal L^{-1} \{F(s)\}, which is a nontrivial task. However, if we complete the square on the denominator,

\displaystyle \frac 4{s^2 + 2s + 2} = \frac 4{(s^2 + 2s + 1) + 1} = \frac 4{(s+1)^2 + 1^2},

then

\begin{aligned} f(t) = \mathcal L^{-1} \{F(s)\} &= \mathcal L^{-1} \left\{ \frac 4{(s+1)^2 + 1^2} \right\} = 4 \cdot \mathcal L^{-1} \left\{ \frac 1{(s+1)^2 + 1^2} \right\}. \end{aligned}

Motivated by the shift theorem again, we define G(s+1) = 1/((s+1)^2 + 1^2). Then

f(t) = 4 \cdot \mathcal L^{-1}\{ G(s+1) \} = 4 \cdot e^{-t} g(t),

where

\begin{aligned} g(t) = \mathcal L^{-1}\{ G(s) \} &= \mathcal L^{-1} \left\{ \frac 1{s^2 + 1^2} \right\} = \sin(t), \end{aligned}

so that f(t) = 4e^{-t} \sin(t). Replacing t with t-2 yields the final answer

\displaystyle \begin{aligned} \mathcal L^{-1} \left\{ \frac{4e^{-2s}}{s^2 + 2s + 2} \right\} &= f(t-2) U(t-2) \\ &= 4 e^{-(t-2)} \sin(t-2) \cdot U(t-2). \end{aligned}

—Joel Kindiak, 19 Apr 25, 1859H

,

Published by

joelkindiak

Leave a comment