KindiakMath

Constructing Real Trigonometry

Let’s properly discuss classical trigonometry. For a novel approach using rational trigonometry, see this post. Assume that the notion of an angle is well-defined.

Definition 1. Consider the following right-angled triangle with acute angle \theta \in (0, \pi/2). Here and subsequently, we adopt the radian notation for angles that stipulates 2\pi = 360^{\circ}.

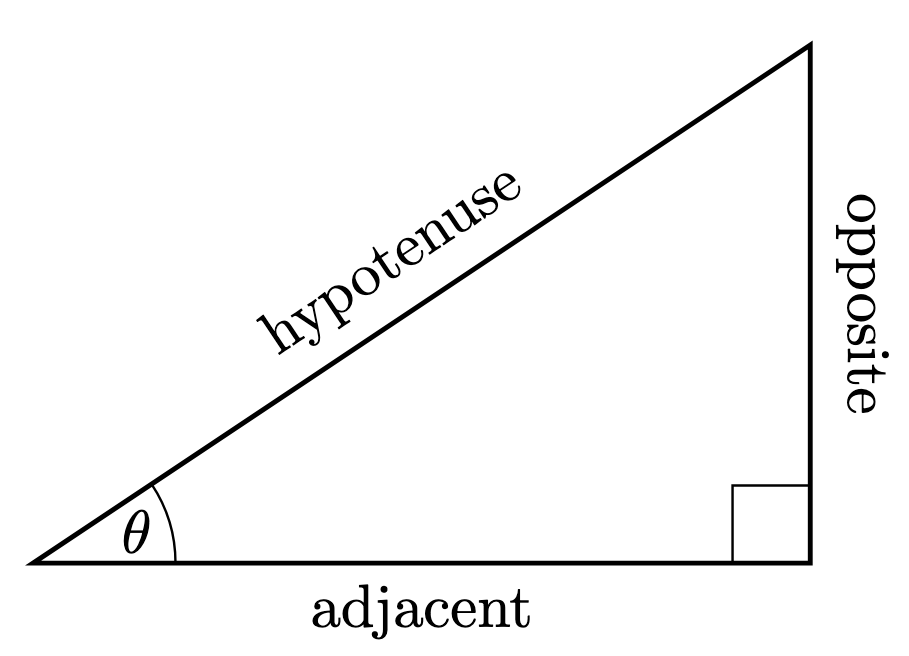
We abbreviate the words opposite, adjacent, and hypotenuse. We define the sine, cosine, and tangent of \theta as follows:

\begin{aligned} \sin(\theta) := \frac{\text{opp}}{\text{hyp}}, \quad \cos(\theta) := \frac{\text{adj}}{\text{hyp}}, \quad \tan(\theta) := \frac{\text{opp}}{\text{adj}}. \end{aligned}

Example 1. By considering the 1–\sqrt{3}–2 and 1–1–\sqrt 2 right triangles, we have the following trigonometric ratios for special angles:

\begin{aligned}\theta = \pi/6:&\quad \sin(\pi/6) = \frac{1}2,\quad \cos(\pi/6) = \frac {\sqrt{3}}2,\quad \tan(\pi/6) = \frac 1{\sqrt 3}. \\ \theta = \pi/4:&\quad \sin(\pi/4) = \frac 1{\sqrt 2},\quad \cos(\pi/4) = \frac 1{\sqrt 2} ,\quad \tan(\pi/4) = 1. \\ \theta = \pi/3:&\quad \sin(\pi/3) = \frac {\sqrt 3}2,\quad \cos(\pi/3) = \frac 12,\quad \tan(\pi/3) = \sqrt 3.\end{aligned}

The case \theta = \pi/4 will play a crucial role for us later. Denote \sin^2(\theta) := (\sin(\theta))^2 for brevity. We will not care too much about the tangent function, since it is connected to sine and cosine in the following way:

Theorem 1. Let \theta \in (0, \pi/2). Then

\displaystyle \sin^2(\theta) + \cos^2(\theta) = 1,\quad \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)},\quad \cos(\theta) = \sin(\pi/2 - \theta).

Proof. For the first identity, use Pythagoras’ theorem to obtain

\displaystyle \sin^2(\theta) + \cos^2(\theta) = \frac{\text{opp}^2}{\text{hyp}^2} + \frac{\text{adj}^2}{\text{hyp}^2} = \frac{\text{opp}^2 + \text{adj}^2}{\text{hyp}^2} = \frac{\text{hyp}^2}{\text{hyp}^2} = 1.

For the second identity, we observe that

\displaystyle \frac{\sin(\theta)}{\cos(\theta)} = \frac{\text{hyp} \cdot \sin(\theta)}{\text{hyp} \cdot \cos(\theta)} = \frac{\text{opp}}{\text{adj}} = \tan(\theta).

For the last identity, since the complementary angle is \pi/2-\theta,

\displaystyle \sin(\pi/2 - \theta) = \frac{\text{adj}}{\text{hyp}} = \cos(\theta).

Strictly speaking, the cosine function is effectively a mutation of the sine function, and so we could technically do all of trigonometry in terms of sine. However, cosine does have its uses and will play a crucial role in our discussions moving forward.

There are many trigonometric identities built off the first two identities, and we will leave them as exercises in algebraic manipulation. For a serious study of trigonometry, we have to ask the all-important question: what is \sin(\theta) if \theta is not acute? In particular, what is a sensible definition for \sin(\pi/2)? The answer to the latter question turns out to answer the former question.

Theorem 2. Let A,B be acute angles. If A + B is acute, then

\begin{aligned} \sin(A+B) &= \sin(A) \cos(B) + \cos(A) \sin(B), \\ \cos(A + B) &= \cos(A) \cos(B) - \sin(A) \sin(B). \end{aligned}

Proof. Consider the following diagram for the proof of both identities.

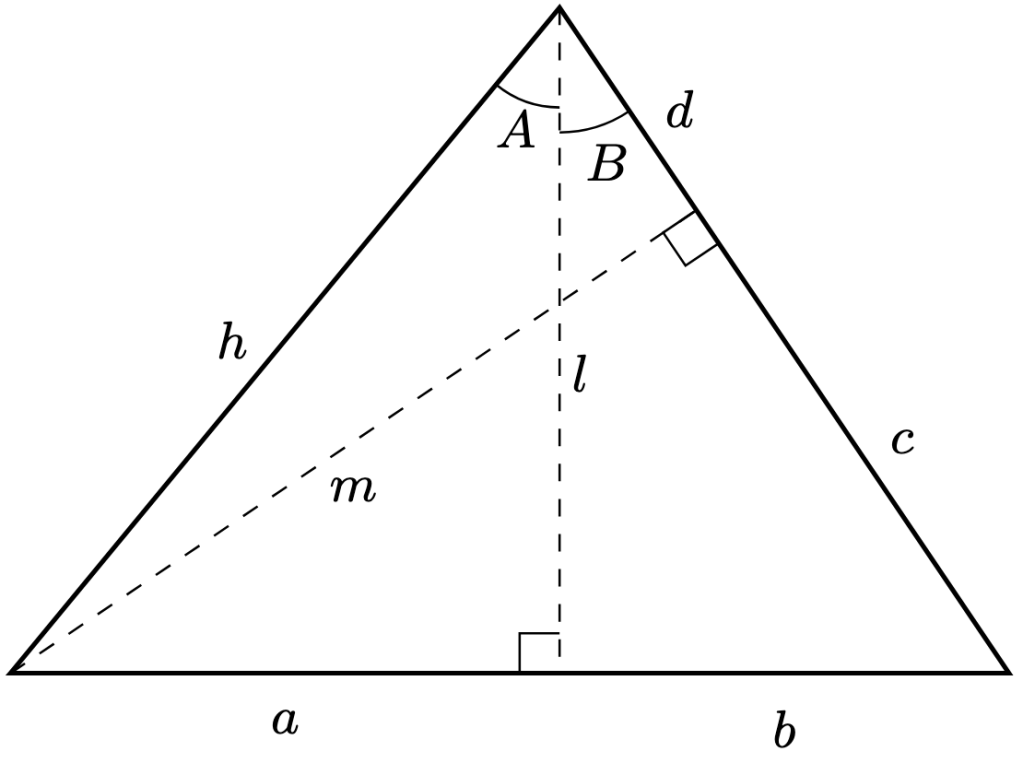
The first identity corresponds to finding an alternate expression for \sin(A+B) = m/h, and the second identity corresponds to finding an alternate expression for \cos(A+B) = d/h. The ratios of interest are

\displaystyle \sin(A) = \frac ah,\quad \cos(A) = \frac lh,\quad \sin(B) = \frac b{c+d},\quad \cos(B) = \frac l{c+d}.

By considering the area of the whole triangle using the bases (a+b) and (c+d) respectively,

\frac 12 \cdot (c + d)\cdot m = \frac 12 \cdot a\cdot l + \frac 12 \cdot b\cdot l.

Dividing by \frac 12 (c+d)h on both sides,

\displaystyle \frac mh = \frac ah \cdot \frac l{c+d} + \frac lh \cdot \frac b{c+d}.

By basic trigonometric ratios,

\sin(A+B) = \sin(A) \cos(B) + \cos(A) \sin(B).

For the second identity, by the Pythagorean theorem,

(a+b)^2 - c^2 = m^2 = h^2 - d^2.

By algebruh,

c^2 = ((c+d) - d)^2 = (c+d)^2 - 2(c+d)d + d^2.

Therefore,

(a^2 + 2ab + b^2) - (c+d)^2 + 2(c+d)d - d^2 = h^2 - d^2.

Simplifying the equation,

2(c+d)d = (h^2 - a^2) + ((c+d)^2 - b^2) - 2ab.

By Pythagoras’ theorem, h^2 - a^2 = (c+d)^2 - b^2 = l^2, so that

2(c+d)d =2l^2 - 2ab.

Dividing by 2(c+d)h on both sides,

\displaystyle \frac dh = \frac{l}{h} \cdot \frac{l}{c+d} - \frac{a}{h} \cdot \frac{b}{c+d}.

By basic trigonometric ratios,

\cos(A+B) = \cos(A) \cos(B) - \sin(A) \sin(B).

Corollary 1. Let \theta be acute. If 2\theta is acute, then

\begin{aligned} \sin(2\theta) = 2\sin(\theta) \cos(\theta), \quad \cos(2\theta) = \cos^2(\theta) - \sin^2(\theta). \end{aligned}

Proof. Set A = B = \theta in Theorem 2.

The key insight is the following: as long as the right-hand side is well-defined, so is the left-hand side. This is our strategy to define \sin and \cos on all of \mathbb R. Let’s systematise our plan.

Definition 1. For any subset I \subseteq \mathbb R, let \phi(I) be the proposition that for any A, B \in I, \sin(A+B) and \cos(A + B) are well-defined, and

\begin{aligned} \sin(A+B) &= \sin(A) \cos(B) + \cos(A) \sin(B), \\ \cos(A + B) &= \cos(A) \cos(B) - \sin(A) \sin(B). \end{aligned}

Write \phi(I) to abbreviate the proposition “\phi(I) is true”. Our overarching goal is to provide sensible definitions for \sin and \cos such that \phi(\mathbb R). By Theorem 1, we have established \phi((0, \pi/8]) and Corollary 1 will help us “double” our results to achieve the massive sub-goal of \phi(\mathbb R^+).

Theorem 3. For any a > 0, suppose \sin and \cos are well-defined on (0, 2a]. For any \theta \in (0, 4a], denote \theta_2 := \theta/2 \in (0, 2a] and define

\sin(\theta) := 2 \sin(\theta_2) \cos(\theta_2),\quad \cos(\theta) := \cos^2(\theta_2) - \sin^2(\theta_2).

If \phi((0, a]), then \phi((0, 2a]).

Proof. Fix A,B \in (0, 2a]. Then A+B \in (0, 4a]. Observe that

(A+B)_2 = A_2 + B_2 \in (0, 2a],

so that A_2,B_2 \in (0, a] and

\begin{aligned} \sin(A+B) &= 2 \sin(A_2 + B_2) \cos(A_2 + B_2).\end{aligned}

Since \phi((0, a]), expanding the right-hand side yields

\begin{aligned}\sin(A_2 + B_2) &= \sin(A_2) \cos(B_2) + \cos(A_2) \sin(B_2), \\ \cos(A_2 + B_2) &= \cos(A_2) \cos(B_2) - \sin(A_2) \sin(B_2).\end{aligned}

On the other hand,

\begin{aligned} \sin(A)\cos(B) &= 2 \sin(A_2)\cos(A_2) (\cos^2(B_2) - \sin^2(B_2)), \\ \sin(B)\cos(A) &= 2 \sin(B_2)\cos(B_2) (\cos^2(A_2) - \sin^2(A_2)). \end{aligned}

With careful algebraic expansion, we will obtain

\sin(A + B) = \sin(A)\cos(B) + \cos(A) \sin(B).

Similarly, we will obtain

\cos(A + B) = \cos(A) \cos(B) - \sin(A) \sin(B).

Corollary 2. \phi(\mathbb R^+). In particular, we have the following special angles:

\begin{aligned} \theta = \pi/2:&\quad \sin(\pi/2) = 1,\quad \cos(\pi/2) = 0 \\ \theta = \pi:&\quad \sin(\pi) = 0,\quad \cos(\pi) = -1. \\ \theta = 2\pi:&\quad \sin(2\pi) = 0,\quad \cos(2\pi) = 1.\end{aligned}

Proof. Fix A,B \in \mathbb R^+. Then there exists N \in \mathbb N such that A+B \in (0, 2^N \cdot \pi/8]. Using induction, we can prove that \phi((0, 2^N \cdot \pi/8]). Therefore, \sin, \cos are well-defined on \mathbb R^+ and the identities

\begin{aligned} \sin(A+B) &= \sin(A) \cos(B) + \cos(A) \sin(B), \\ \cos(A + B) &= \cos(A) \cos(B) - \sin(A) \sin(B), \end{aligned}

hold for any A, B \in \mathbb R^+. Hence, \phi(\mathbb R^+), as required.

Corollary 3. For any \theta > 0,

\sin(\theta + 2\pi) = \sin(\theta),\quad \cos(\theta + 2\pi) = \cos(\theta).

Furthermore, for any positive integer n,

\sin(\theta + n \cdot 2\pi) = \sin(\theta),\quad \cos(\theta + n \cdot 2\pi) = \cos(\theta).

We have done a remarkable task: defining \sin, \cos on \mathbb R^+ and proving that they satisfy the desired addition formulae. But we haven’t proven this case for all of \mathbb R, since \mathbb R = \mathbb R^- \sqcup \{0\} \sqcup \mathbb R^+. Surprisingly, though, Corollary 3 gives us a unique insight. Observe that for \theta \in (-2\pi, 0], \sin(\theta +2\pi) and \cos(\theta + 2\pi) are well-defined expressions. This means we can do a “reverse” definition for non-positive \theta.

Theorem 4. For any \theta \leq 0, let n_\theta denote any integer such that \theta + n_\theta \cdot 2\pi > 0. The notions

\sin(\theta) := \sin(\theta + n_\theta \cdot 2\pi),\quad \cos(\theta) := \cos(\theta + n_\theta \cdot 2\pi)

are well-defined by Corollary 3. Then \phi(\mathbb R). In particular,

\sin(0) = \sin(2\pi) = 0,\quad \cos(0) = \cos(2\pi) = 1.

Proof. Fix A, B \in \mathbb R. Find n_A, n_B \in \mathbb N such that A +n_A \cdot 2\pi > 0 and B+n_B \cdot 2\pi > 0. Then (A+B) + (n_A + n_B) \cdot 2\pi > 0 so that \phi(\mathbb R^+) allows

\begin{aligned} \sin(A+B) &= \sin((A+B) + (n_A + n_B) \cdot 2\pi) \\ &= \sin((A + n_A \cdot 2\pi) + (B + n_B \cdot 2\pi)) \\ &= \sin(A + n_A \cdot 2\pi) \cos(B + n_B \cdot 2\pi) \\ &\phantom{==} + \cos(A + n_A \cdot 2\pi) \sin(B + n_B \cdot 2\pi) \\ &= \sin(A) \cos(B) + \cos(A) \sin(B). \end{aligned}

A similar calculation yields

\cos(A + B) = \cos(A) \cos(B) - \sin(A) \sin(B).

Thus, we have properly defined \sin and \cos on all of \mathbb R, and even proved that the identities

\begin{aligned} \sin(A+B) &= \sin(A) \cos(B) + \cos(A) \sin(B), \\ \cos(A + B) &= \cos(A) \cos(B) - \sin(A) \sin(B), \end{aligned}

are well-defined and hold for any A, B \in \mathbb R. From these two key identities, we obtain all other trigonometric identities commonly obtained in tables of mathematical formulas.

—Joel Kindiak, 4 Jun 25, 1758H

,

Published by

joelkindiak

Leave a comment