H2 Math 2025 Suggested Answers (Paper 1)

Questions have not been uploaded due to copyright reasons. Do comment if you spot any errors.

Question 1. Sequences and Series

Solution. (a) Setting $r = 1, 2, 3$ ,

$\begin{aligned} u_2 &= 3 u_1 + 5 = 3a + 5, \\ u_3 &= 3u_2 + 5 = 3(3a+5) + 5 = 9a + 20 \\ u_4 &= 3u_3 + 5 = 3(9a + 20) + 5 = 27a + 65.\end{aligned}$

(b) Using summation notation,

$\begin{aligned}110 = \sum_{r=1}^4 u_r &= u_1 + u_2 + u_3 + u_4 \\ &= a + (3a+5) + (9a+20) + (27a+65) \\ &= 40a + 90.\end{aligned}$

Solving the equation yields $a = 1/2$ .

Question 2. Arithmetic and Geometric Progression

Solution. (a) Let $u_n = a + (n-1)d$ denote the $n$ -th term of the arithmetic sequence, $n \geq 1$ . By considering the sum of the first $20$ terms, we have first term $a$ and last term $a + 19d$ so that

$\displaystyle \frac{20}{2} (a + (a+19d)) = 65 \quad \Rightarrow \quad 2a + 19d = 6.5.$

For the next $8$ terms, we have first term $a + 20d$ and last term $a + 27d$ so that

$\displaystyle \frac 82 ((a+20d) + (a + 27d)) = -30 \quad \Rightarrow \quad 2a + 47d = -7.5.$

Solving the system of linear equations yields $a = 8$ and $d = -1/2$ .

(b) By considering the ratio of consecutive terms,

$\begin{aligned} \frac{u_{n+1}}{u_n} = \frac{e^{k(n+2)}}{e^{k(n+1)}} = e^{k(n+2) - k(n+1)} = e^k \neq 1, \end{aligned}$

which is constant. Therefore, the sequence having a common ratio $e^k$ is a geometric sequence.

Question 3. Complex Numbers

Solution. (a) We first compute the modulus and argument of $\sqrt 3 \pm i$ :

$|\sqrt 3 \pm i| = \sqrt{(\sqrt 3)^2 + (\pm 1)^2} = 2,\quad \arg(\sqrt 3 \pm i) = \pm \frac 16 \pi.$

Therefore,

$\begin{aligned} |z| &= \frac{|\sqrt 3 + i|}{|\sqrt 3 - i|} = \frac{2}{2} = 1,\\ \arg(z) &= \arg(\sqrt 3 + i) - \arg(\sqrt 3 - i) \\ &= \textstyle \frac 16 \pi - \left(-\frac 16 \pi\right) = \frac 13 \pi. \end{aligned}$

(b) The Argand diagram is drawn below.

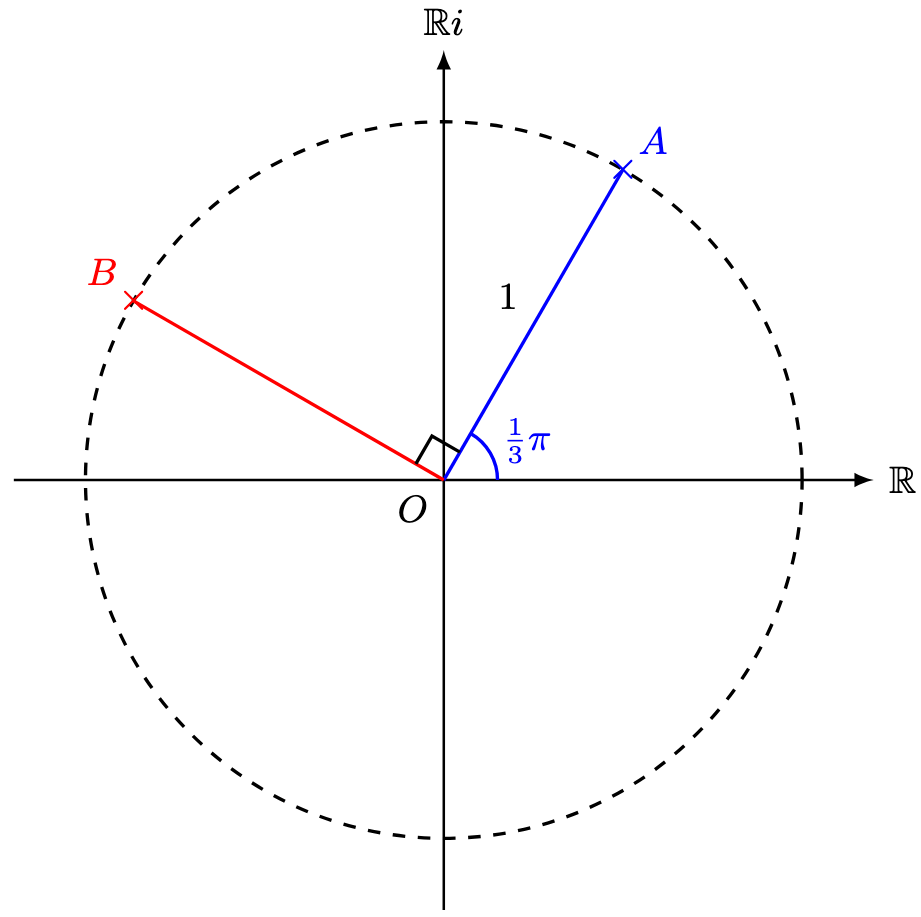
The point $B$ represents the complex number $iz$ .

Question 4. Optimisation

Solution. (a) We first write the function as $y = (3x+10)(x+1)^{-1/2}$ . Using the product rule,

$\begin{aligned} \frac{\mathrm dy}{\mathrm dx} &= \textstyle 3 \cdot (x+1)^{-1/2} + (3x+10) \cdot \left(-\frac 12 \right) (x+1)^{-3/2} \\ &=\textstyle \frac 12(x+1)^{-3/2} \left( 2 \cdot 3 \cdot (x+1) + (3x+10) \cdot (-1) \right) \\ &=\textstyle \frac 12(x+1)^{-3/2} \left( 6x+6 - (3x+10) \right) \\ &=\textstyle \frac 12(x+1)^{-3/2} ( 3x - 4).\end{aligned}$

At the turning point, $\displaystyle \frac{\mathrm dy}{\mathrm dx} = 0$ so that

$\textstyle \frac 12(x+1)^{-3/2} ( 3x - 4) = 0 \quad \Rightarrow \quad x = \frac 43.$

(b) We use the product rule again to obtain

$\begin{aligned} \frac{\mathrm d^2y }{\mathrm dx^2} &= \textstyle \frac 12 \left( -\frac 32 \cdot (x+1)^{-5/2} ( 3x - 4) + (x+1)^{-3/2} \cdot 3 \right).\end{aligned}$

At the turning point, $x = 4/3$ yields

$\begin{aligned} \frac{\mathrm d^2 y }{\mathrm dx^2} \Big|_{x=4/3} &= \textstyle \frac 12 \left( 0 + (\frac 43+1)^{-3/2} \cdot 3 \right) = \frac 32 \cdot \left( \frac 73 \right)^{-3/2} \approx 0.421 > 0.\end{aligned}$

Hence, the turning point is a local minimum.

Question 5. Inequalities

Solution. (a) Make the substitution $u = e^x > 0$ , so that we solve the inequality

$\begin{aligned} u &\geq 2u^{-1} + 1 \\ u^2 & \geq 2 + u \\ u^2 - u - 2 &\geq 0 \\ (u-2)(u+1) &\geq 0. \end{aligned}$

Therefore, $u \leq -1$ (which we reject since $u > 0$ ) or

$u-2 \geq 0 \quad \Leftrightarrow \quad u \geq 2\quad \Leftrightarrow \quad e^x \geq 2 \quad \Leftrightarrow \quad x \geq \ln 2.$

(b) By part (a),

$x \geq \ln 2 \quad \Leftrightarrow \quad e^x \geq 2e^{-x} + 1 \quad \Leftrightarrow \quad e^x - 2e^{-x} - 1 \geq 0.$

We first calculate the indefinite integral for convenience:

$\displaystyle f(x) := \int (e^x - 2e^{-x} - 1)\, \mathrm dx = e^x + 2e^{-x} - x + C.$

Since $\ln 2 \approx 0.693 \in (0, 1)$ , we split the integral into two parts:

$\begin{aligned} \int_0^1 |e^x - 2e^{-x} - 1|\, \mathrm dx &= -\int_0^{\ln 2} (e^x - 2e^{-x} - 1)\, \mathrm dx + \int_{\ln 2}^{1} (e^x - 2e^{-x} - 1)\, \mathrm dx \\ &= -(f(\ln 2) - f(0)) + (f(1) - f(\ln 2)) \\ &= f(1) - 2 f(\ln 2) + f(0) \\ &= (e^1 + 2e^{-1} - 1) - 2 (e^{\ln 2} + 2e^{-\ln 2} - \ln 2) + (1 + 2 - 0) \\ &= (e + 2/e - 1) - (6 - 2\ln 2) + 3 \\ &= e + 2/e + 2\ln 2 - 4.\end{aligned}$

Question 6. Radioactive Decay

Solution. (a) Using the method of separable variables,

$\begin{aligned} \int \frac{1}{M}\, \mathrm dM &= \int -k\, \mathrm dt \\ \ln |M| &= -kt + C \\ M &= \pm e^C \cdot e^{-kt} \\ &= Ae^{-kt}.\end{aligned}$

By the question, setting $t = 0$ yields

$M_0 = Ae^{-k\cdot 0} = A \quad \Rightarrow \quad M = M_0 \cdot e^{-kt}.$

Furthermore, $M = M_0/2$ when $t = 5730$ :

$\begin{aligned} \frac{M_0}{2} &= M_0 \cdot e^{-k \cdot 5730} \\ \frac 12 &= e^{-5730 k} \\ k &= \frac{\ln 2}{5730} \approx 1.21 \times 10^{-4}. \end{aligned}$

(b) Letting $T$ denote the time passed (in years), we solve the equation

$\begin{aligned} 0.2M_0 &= M_0 \cdot e^{-kT} \\ T &= \frac{ \ln 0.2 }{-k} \\ &= \ln 0.2 \cdot \left( - \frac{5730}{\ln 2} \right) \\ &= 13\, 304 \\ &\approx 13\, 300. \end{aligned}$

Therefore the plant died $13\, 300$ years ago, correct to 3 significant figures.

Question 7. Volume of Revolution

Solution. (a) Using linearity and the product rule,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (x \ln x - x ) &= \frac{\mathrm d}{\mathrm dx}(x \ln x) - \frac{\mathrm d}{\mathrm dx}(x) \\ &= 1 \cdot \ln x + x \cdot \frac 1x - 1 \\ &= \ln x. \end{aligned}$

(b) Using (a),

$\displaystyle \int \ln x\, \mathrm dx = x \ln x - x + C.$

At the $x$ -axis, $\ln x = 0 \Rightarrow x = 1$ . Therefore, the required volume of revolution $V_1$ is

$\begin{aligned}V_1 &= \pi \int_1^e (\ln x)^2\, \mathrm dx \\ &= \pi \left( \left[\underbrace{ (x \ln x - x) }_{\mathrm I} \cdot \underbrace{ \ln x }_{\mathrm S}\right]_1^e - \int_1^e \underbrace{ (x \ln x - x) }_{\mathrm I} \cdot \underbrace{ \frac 1x }_{\mathrm D}\, \mathrm dx \right) \\ &= \pi \left( (0 - 0) - \int_1^e (\ln x - 1)\, \mathrm dx \right) \\ &= \pi \int_1^e (1 - \ln x )\, \mathrm dx \\ &= \pi [ x - (x \ln x - x)]_1^e \\ &= \pi [ 2x - x \ln x ]_1^e \\ &= \pi \cdot ( (2e - e) - (2 - 0) ) \\ &= \pi (e-2)\, \text{units}^3.\end{aligned}$

(c) The curve $y = \ln(x)$ is equivalently given by $x = e^y$ . Therefore, the required volume of revolution $V_2$ is

$\begin{aligned} V_2 &= \pi e^2 \cdot 1 - \pi \int_0^1 (e^y)^2\, \mathrm dy \approx 13. 18\, \text{units}^3\, (\text{2dp}). \end{aligned}$

Remark 1. The exact volume for $V_2$ is $V_2 = \frac 12\pi (e^2 + 1)\, \text{units}^3$ , left as a simple exercise in integration.

Question 8. Vectors

Solution. (a) We first write $\pi_1$ in scalar product form:

$\pi_1 : \mathbf r \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} = 2.$

The line $\ell$ perpendicular to $\pi_1$ passing through $P$ has vector equation

$\ell : \mathbf r = \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix},\quad \lambda \in \mathbb R.$

The foot of perpendicular $F$ is given by the intersection of $\ell$ and $\pi_1$ :

$\begin{aligned} \left( \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \right) \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} &= 2 \\ \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} &= 2 \\ -5 +14 \lambda &= 2 \\ \lambda &= \textstyle \frac 12.\end{aligned}$

Therefore,

$\overrightarrow{OF} = \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \frac 12 \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3/2 \\ 3/2 \end{bmatrix}\quad \Rightarrow \quad F(-2, 3/2, 3/2).$

(b) Let $Q$ denote the reflection of $P$ in $\pi_1$ . By the midpoint theorem,

$\overrightarrow{OF} = \frac 12 (\overrightarrow{OP} + \overrightarrow{OQ}).$

Therefore,

$\begin{aligned} \overrightarrow{OQ} &= 2 \overrightarrow{OF} - \overrightarrow{OP} = 2 \begin{bmatrix} -2 \\ 3/2 \\ 3/2 \end{bmatrix} - \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \\ 3 \end{bmatrix}. \end{aligned}$

(c) The normal vector of $\pi_2$ is given by the cross product:

$\begin{bmatrix} 2 \\ -1 \\ 5 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix}.$

The acute angle $\alpha$ between $\pi_1, \pi_2$ is given by the dot product between their normal vectors:

$\begin{aligned} \left|\begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \cdot \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix} \right| &= \left\| \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \right\| \left\| \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix} \right\| \cos \alpha \\ 4 &= \sqrt{14} \sqrt{221} \cos \alpha \\ \cos \alpha &= \frac{4}{\sqrt{14}\sqrt{221} } \\ \alpha &\approx 85.9^\circ. \end{aligned}$

Question 9. Power Series

Solution. (a) Using implicit differentiation,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (\sin y) &= \frac{\mathrm d}{\mathrm dx}(px) \\ \cos y \cdot \frac{\mathrm dy}{\mathrm dx} &= p \\ \frac{\mathrm dy}{\mathrm dx} &= \frac{p}{\cos y} \\ &= p \sec y.\end{aligned}$

(b) Using implicit differentiation two more times,

$\begin{aligned} \frac{\mathrm d^2 y }{\mathrm dx^2} &= p \cdot \sec y \tan y \cdot \frac{\mathrm dy}{\mathrm dx} \\ &= \tan y \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^2 \\ \frac{\mathrm d^3 y}{\mathrm dx^3} &= \sec^2 y \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^2 + \tan y \cdot 2 \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm d^2 y}{\mathrm dx^2} \\ &= \sec^2 y \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^3 + 2\tan y \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm d^2 y}{\mathrm dx^2}. \end{aligned}$

Setting $x = 0$ ,

$\begin{aligned} y &= \sin^{-1} 0 = 0, \\ \frac{\mathrm dy}{\mathrm dx} &=p \sec 0 = p, \\ \frac{\mathrm d^2 y }{\mathrm dx^2} &= \tan 0 \cdot p^2 = 0, \\ \frac{\mathrm d^3 y }{\mathrm dx^3} &= \sec^2 0 \cdot p^3 + 2\tan 0 \cdot p \cdot 0 = p^3. \end{aligned}$

Therefore, the Maclaurin series for $y$ up to and including the term in $x^3$ is given by

$\displaystyle y \approx 0 + px + \frac{0}{2!} \cdot x^2 + \frac{p^3}{3!} \cdot x^3 = px + \frac{p^3}{6} \cdot x^3.$

(c) Differentiating term-by-term,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (\sin^{-1} px) &\approx \frac{\mathrm d}{\mathrm dx} \left( px + \frac{p^3}{6} \cdot x^3 \right) \\ \frac 1{\sqrt{1 - (px)^2}} \cdot p &\approx p + \frac{p^3}{6} \cdot 3x^2 \\ \frac 1{\sqrt{1 - p^2 x^2}} &\approx 1 + \frac{p^2}{2} \cdot x^2. \end{aligned}$

Setting $p = 3$ (so that $p^2 = 9$ ) yields the series expansion

$\displaystyle \frac 1{\sqrt{1 - 9x^2}} \approx 1 + \frac 92 \cdot x^2.$

Question 10. Functions

Solution. (a) The graph has asymptotes $y = -a$ , $x = -b$ and axial intercepts $(4/a, 0)$ , $(0, 4/b)$ .

(b) We first use algebra (or long division) to obtain

$\displaystyle f(x) =\frac{4-ax}{x+b} = -a + \frac{4+ ab}{x+b}.$

Therefore, we make the following transformations:

Translate by $a$ units in the positive $y$ -direction.
Scale by a factor of $1/(4+ab)$ parallel to the $y$ -axis.
Translate by $b$ units in the positive $x$ -direction.

(c) Denote $y = f^{-1}(x) \Leftrightarrow x = f(y)$ so that

$\begin{aligned}x &= -a + \frac{4+ab}{y+b} \\ x+a &= \frac{4+ab}{y+b} \\ y+b &= \frac{4+ab}{x+a} \\ y &= -b + \frac{4 + ab}{x+a} \\ f^{-1}(x) &= -b + \frac{4 + ab}{x+a}.\end{aligned}$

Furthermore, $\text{R}_{f^{-1}} = \text{D}_{f} = (-\infty, -b) \cup (-b, \infty) \equiv \mathbb R \backslash \{-b\}$ .

(d) Given $b = a$ ,

$\displaystyle f^{-1}(x) = -a + \frac{4+a^2}{x+a} = f(x) \quad \Rightarrow \quad f^2(x) = x.$

Since $2025 = 2 \cdot 1012 + 1$ ,

$\displaystyle f^{2025}(2) = f(2) = -a + \frac{4+a^2}{2+a}.$

Question 11. Roller Coaster

Solution. (a) Differentiating with respect to $\theta$ ,

$\begin{aligned} \frac{\mathrm dx}{\mathrm d\theta} &= 28 \cdot (\cos \theta + \theta \cdot (-\sin \theta ) ) \\ &= 28 (\cos \theta - \theta \sin \theta ),\\ \frac{\mathrm dy}{\mathrm d\theta} &= 20 \cdot ( - (1 \cdot \sin \theta + \theta \cdot \cos \theta ) ) \\ &= -20(\sin \theta + \theta \cos \theta ). \end{aligned}$

By an application of the chain rule,

$\displaystyle \frac{\mathrm dy}{\mathrm dx} = \frac{-20(\sin \theta + \theta \cos \theta )}{ 28 (\cos \theta - \theta \sin \theta ) } = -\frac{5(\sin \theta + \theta \cos \theta )}{ 7 (\cos \theta - \theta \sin \theta ) }.$

(b) (i) At $C$ and $D$ , the denominator of $\displaystyle \frac{\mathrm dy}{\mathrm dx}$ is $0$ :

$\displaystyle 7 (\cos \theta - \theta \sin \theta ) = 0 \quad \Rightarrow \quad \cos \theta = \theta \sin \theta .$

Therefore, $\theta = \pm 0.8603 \approx \pm 0.86\ (\text{2sf})$ .

(b) (ii) The $x$ -coordinates of $C,D$ are $12.289$ and $43.710$ respectively. Hence,

$CD = 43.710 - 12.289 = 31.421 \approx 31.4\, \text{units}.$

(c) (i) We solve the equation

$28(\theta \cos \theta + 1) = 28 \quad \Rightarrow \quad \theta \cos \theta = 0.$

Therefore, $\theta = 0$ or $\cos \theta = 0\Rightarrow \theta = \pm \pi/2$ . By substituting into expression for $y$ ,

$\displaystyle y = 10(4 - \pi), 40, 10(4-\pi)$

respectively. Hence, $\theta = 0$ at $A$ .

(c) (ii) Furthermore, $\theta = \pm \pi/2$ at $B$ .

(c) (iii) Consequently, $AB = 40 - (10(4-\pi)) = 10\pi \approx 31.4\, \text{units}$ .

(d) The $y$ -coordinates of $E$ and $D$ are equal:

$\displaystyle y = 20(2 - 0.8603 \sin 0.8603 ) = 26.957.$

Therefore, $AE = 40 - 26.957 = 13.042$ . Since

$\frac 12 CD = \frac 12 \cdot 31.421 = 15.7105,$

the margin of error $\epsilon$ is given by

$\epsilon := 10\% \cdot \frac 12 CD = 0.1 \cdot 15.7105 = 1.57105.$

In particular, we require

$AE \in (\frac 12 CD - \epsilon, \frac 12 CD + \epsilon) = (14.13945, 17.28155),$

which does not hold. In particular, this section of the track does not satisfy the safety condition.

Question 12. Complex Numbers

(a) Since the coefficients of the given polynomial equation are all real, by the conjugate root theorem, a second root is given by $1 - 2i$ .

(b) Given $z = 1+2i$ , we evaluate $z^2$ and $z^3$ :

$\begin{aligned} z^2 &= 1^2 + 2 \cdot 1 \cdot 2i + (2i)^2 = -3 + 4i, \\ z^3 &= 1^3 + 3 \cdot 1^2 \cdot 2i + 3 \cdot 1 \cdot (2i)^2 + (2i)^3 \\ &= 1 + 6i - 12 -8i \\ &= -11 - 2i. \end{aligned}$

Therefore, substituting $z = 1+2i$ ,

$\begin{aligned}(1+2i)^3 + p(1+2i)^2 + q(1+2i) - 10 &= 0 \\ (-11 - 2i) + p(-3 + 4i) + q(1+2i) - 10 &= 0 \\ (- 3p + q - 21) + (-2 + 4p + 2q)i = 0. \end{aligned}$