Nontrivial Rates of Change

Big Idea

The rate of change of a quantity $x(t)$ in terms of time $t$ is $\displaystyle \frac{\mathrm dx}{\mathrm dt}$ . Furthermore, given $y \equiv y(x)$ , the chain rule yields

$\displaystyle \frac{\mathrm dy}{\mathrm dt} = \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm dx}{\mathrm dt}.$

Questions

Question 1. The point $P(x, y)$ above the $y$ -axis at time $t$ is defined by the equations

$x = \cos (t), \quad y = \sin (t),\quad 0 \leq t < \pi.$

Define $A(-1, 0)$ . Let $Q$ denote the intersection of $AP$ with the $y$ -axis.

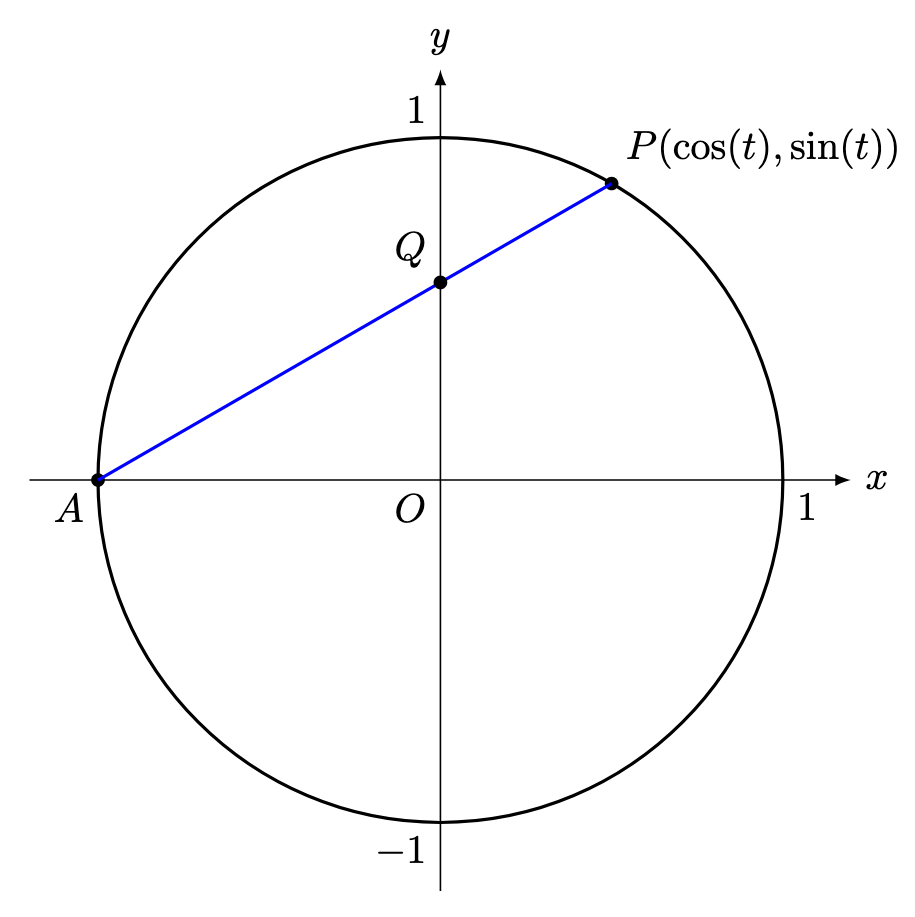
Evaluate the rate of change of the $y$ -coordinate of $Q$ at the point the gradient of the tangent to the curve at $P$ is $-1/\sqrt{3}$ .

(Click for Solution)

Solution. Differentiating with respect to $t$ ,

$\displaystyle \frac{\mathrm dx}{\mathrm dt} = -\sin(t),\quad \frac{\mathrm dy}{\mathrm dt} = \cos(t).$

By the chain rule,

$\begin{aligned} \frac{\mathrm dy}{\mathrm dt} &= \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm dx}{\mathrm dt} \\ \cos(t) &= -\frac 1{\sqrt 3} \cdot -\sin(t)\\ \tan(t) &= \sqrt{3} \\ t &= \pi/3. \end{aligned}$

Let $y_Q$ denote the $y$ -coordinate of $Q$ . The equation of $AP$ is given by

$\displaystyle \frac{ y - 0 }{ x- (-1) } = \frac{\sin(t) - 0}{\cos(t) - (-1)}\quad\Rightarrow \quad y = \frac{\sin(t)}{1 + \cos(t)} \cdot (x+1).$

At the $y$ -axis, $x = 0$ , so that

$\displaystyle y_Q = \frac{\sin(t)}{1 + \cos(t)}.$

Applying the quotient rule,

$\begin{aligned} \frac{\mathrm dy_Q}{\mathrm dt} &= \frac{\mathrm d}{\mathrm dt} \left( \frac{\sin(t)}{1 + \cos(t)} \right) \\ &= \frac{\displaystyle (1 + \cos(t)) \cdot \frac{\mathrm d}{\mathrm dt}(\sin(t)) - \sin(t) \cdot \frac{\mathrm d}{\mathrm dt}(1 + \cos(t))}{( 1 + \cos(t) )^2} \\ &= \frac{(1 + \cos(t)) \cdot \cos(t) - \sin(t) \cdot (0 + (-\sin(t))}{( 1 + \cos(t) )^2} \\ &= \frac{(\cos(t) + \cos^2(t)) + \sin^2(t) }{( 1 + \cos(t) )^2} \\ &= \frac{\cos(t) + (\cos^2(t) + \sin^2(t)) }{( 1 + \cos(t) )^2} \\ &= \frac{ \cos(t) + 1 }{( 1 + \cos(t) )^2} = \frac{ 1 }{ 1 + \cos(t) }. \end{aligned}$

Therefore, at $t = \pi/3$ , since $\cos(t) = 1/2$ ,

$\begin{aligned} \frac{\mathrm dy_Q}{\mathrm dt} &= \frac{ 1 }{ 1 + 1/2 } = \frac 23\, \text{units}/\text{s}. \end{aligned}$

Alternate Solution. Using double-angle formulae,

$\displaystyle y_Q = \frac{\sin(t)}{1 + \cos(t)} = \frac{2 \sin(t/2) \cos (t/2)}{2 \cos^2(t/2)} = \tan(t/2).$

Differentiating,

$\displaystyle \frac{ \mathrm dy_Q }{ \mathrm dt } = \frac 12 \sec^2(t/2).$

The rest of the question follows as per usual.

Question 2. A man of height $1.6\, \text{m}$ metres is currently $300\, \text{m}$ away from a pole of height $3.6\, \text{m}$ . He runs in a straight line towards the pole at a speed of $3\, \text{m}/\text{s}$ . Let $\theta$ denote the angle of elevation from the man to the top of the pole.

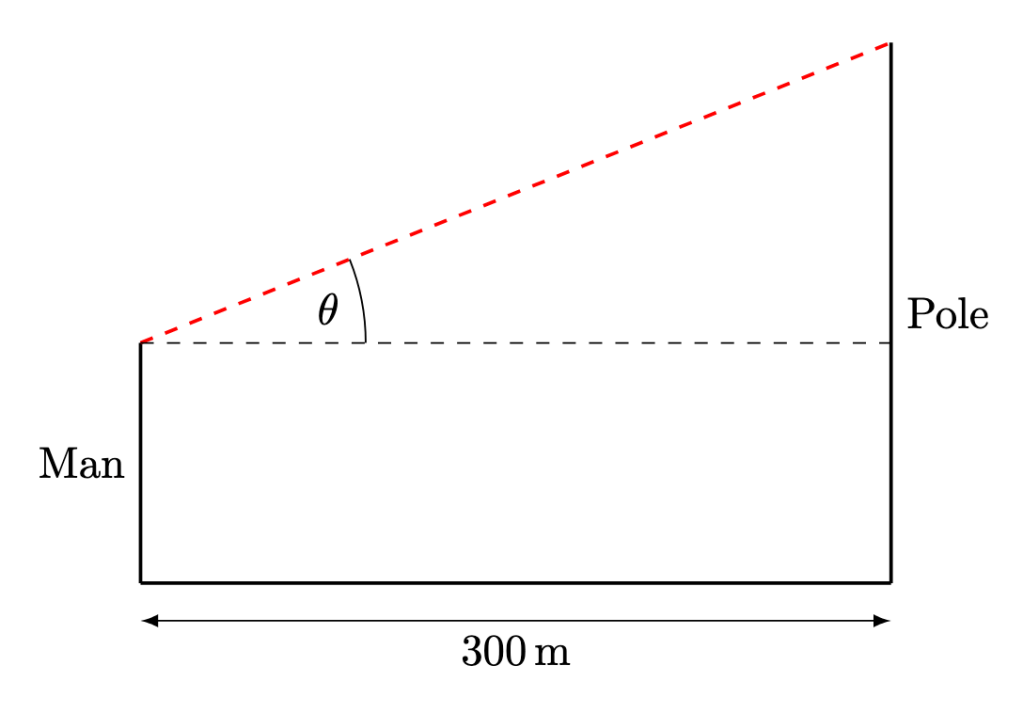
Evaluate the rate of change of $\theta$ when the man is at the pole.

(Click for Solution)

Solution. The man’s distance from the pole at time $t$ is given by $(300 - 3t)$ metres. By considering the height difference between the pole and the man,

$\displaystyle \tan(\theta(t)) = \frac{3.6-1.6}{300 - 3t}\quad \Rightarrow \quad \theta(t) = \tan^{-1}\left( \frac{2}{3(100- t)} \right).$

Applying the chain rule,

$\begin{aligned} \frac{\mathrm d\theta}{\mathrm dt} &= \frac{ \mathrm d }{ \mathrm dt } \left( \tan^{-1}\left( \frac{2}{3(100- t)} \right) \right) \\ &= \frac 1{1 + \left( \frac{2}{3(100- t)} \right)^2} \cdot \frac{\mathrm d}{\mathrm dt}\left( \frac{2}{3(100- t)} \right) \\ &= \frac 1{1 + \frac{4}{9(100- t)^2}} \cdot \frac 23 \cdot \frac{\mathrm d}{\mathrm dt}\left( (100-t)^{-1} \right) \\ &= \frac {9(100- t)^2}{4 + 9(100- t)^2} \cdot \frac 23 \cdot (-1)(100-t)^{-2} \cdot \frac{\mathrm d}{\mathrm dt}(100 - t) \\ &= \frac {9(100- t)^2}{4 + 9(100- t)^2} \cdot \frac 23 \cdot (-1)(100-t)^{-2} \cdot (-1) \\ &= \frac {6}{4 + 9(100- t)^2}. \end{aligned}$

At the pole, $t = 100$ , so that

$\displaystyle \frac{\mathrm d\theta}{\mathrm dt} = \frac 6{4 + 9(100-100)^2} = 1.5\, \text{rad}/\text{s}.$

—Joel Kindiak, 4 Sept 25, 1149H

KindiakMath