Optimised Geometry

Big Idea

To maximise (or minimise) a quantity $y\equiv y(x)$ , we apply the zero derivative condition

$\displaystyle \frac{\mathrm dy}{\mathrm dx} \equiv y'(x) = 0,$

and check that the corresponding value $x = c$ yields to a maximum (resp. minimum) via the second derivative test:

a local maximum is obtained at $c$ when $y''(c) <0$ ,
a local minimum is obtained at $c$ when $y''(c) > 0$ .

Recall that we denote

$\displaystyle y'' \equiv y''(x) := (y')'(x) \equiv \frac{\mathrm d}{\mathrm dx}(y'(x)) = \frac{\mathrm d}{\mathrm dx}\left(\frac{\mathrm dy}{\mathrm dx}\right) =: \frac{\mathrm d^2 y}{\mathrm dx^2}$

for brevity.

Questions

Question 1. Evaluate the area of the largest rectangle contained inside the ellipse graphed below.

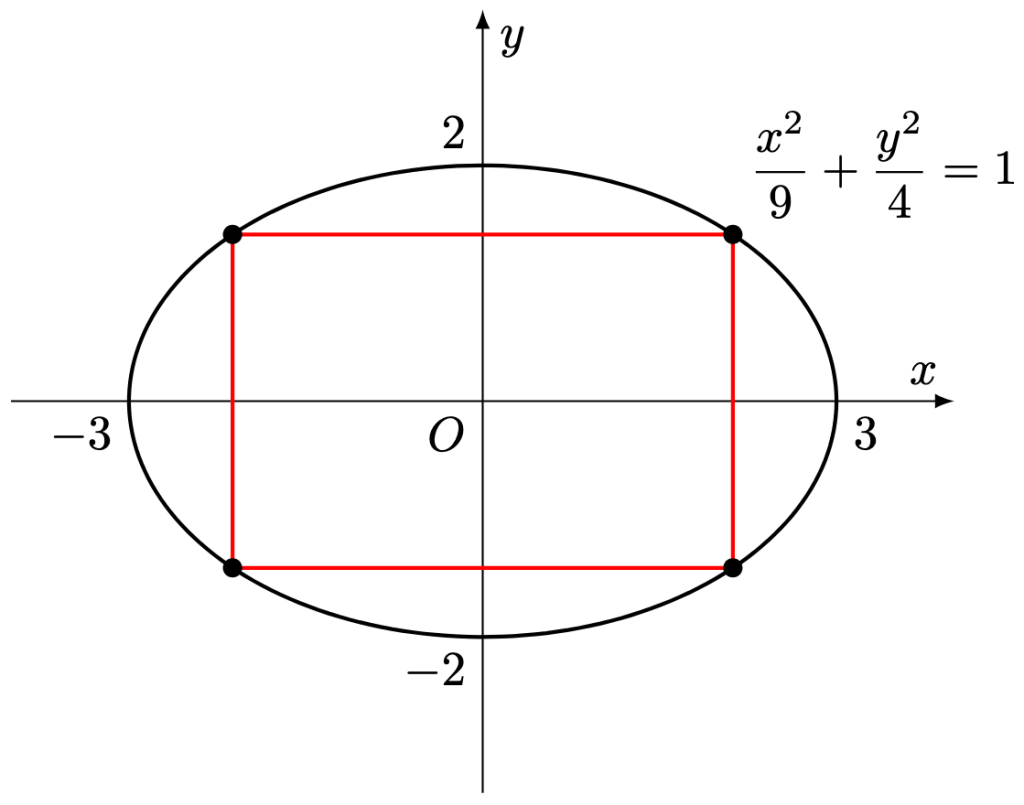
(Click for Solution)

Solution. Given $x, y > 0$ , the base of the rectangle is $2x$ and its height is $2y$ , yielding a total area of $A = 4xy$ . Differentiating with respect to $x$ ,

$\displaystyle \frac{\mathrm dA}{\mathrm dx} = 4y + 4x \cdot \frac{\mathrm dy}{dx}.$

On the other hand, given the ellipse $\displaystyle \frac{x^2}{9} + \frac{y^2}{4} = 1$ , differentiate with respect to $x$ on both sides to obtain

$\displaystyle \frac{2x}{9} + \frac{2y}{4} \cdot \frac{\mathrm dy}{\mathrm dx} = 0 \quad \Rightarrow \quad \frac{\mathrm dy}{\mathrm dx} = -\frac{4x}{9y}.$

Therefore,

$\displaystyle \frac{\mathrm dA}{\mathrm dx} = 4y + 4x \cdot \frac{\mathrm dy}{dx} = 4y - \frac{16x^2}{9y}.$

By the zero-derivative condition, if $A$ is maximised, then $\displaystyle \frac{\mathrm dA}{\mathrm dx} = 0$ :

$\displaystyle 4y - \frac{16x^2}{9y} = 0 \quad \Rightarrow \quad y^2 = \frac{4}{9}x^2.$

Plugging back into the equation of the ellipse,

$\begin{aligned} \frac{x^2}{9} + \frac{1}{4} \cdot \frac{4}{9}x^2 &= 1 \\ x^2 &= 18\\ x &= \sqrt{18} \\ &= 3\sqrt{2}, \end{aligned}$

since $x > 0$ , yielding $y = \frac 23 x = \frac 23 \cdot 3\sqrt 2 = 2\sqrt 2$ . Thus, the area of the corresponding rectangle is $A = 4 \cdot 3\sqrt 2 \cdot 2\sqrt 2 = 12\, \text{units}^2$ .

To apply second derivative test, we differentiate $A$ again:

$\begin{aligned} \frac{\mathrm d^2 A}{\mathrm dx^2} &= 4 \cdot \frac{\mathrm dy}{\mathrm dx} - \frac{16 \cdot 2x \cdot 9y - 16x^2 \cdot \frac{\mathrm dy}{\mathrm dx}}{81y^2} \\ &= 4 \cdot 0 - \frac{16 \cdot 2x \cdot 9y - 16x^2 \cdot 0}{81y^2} \\ &= - \frac{32x }{9y} < 0,\end{aligned}$

so $A$ is indeed maximised when $x = 3\sqrt 2$ and $y = 2\sqrt 2$ .

Question 2. The diagram below shows a movie theatre with a screen $9\, \text{m}$ tall, whose base is $4\, \text{m}$ above the ground.

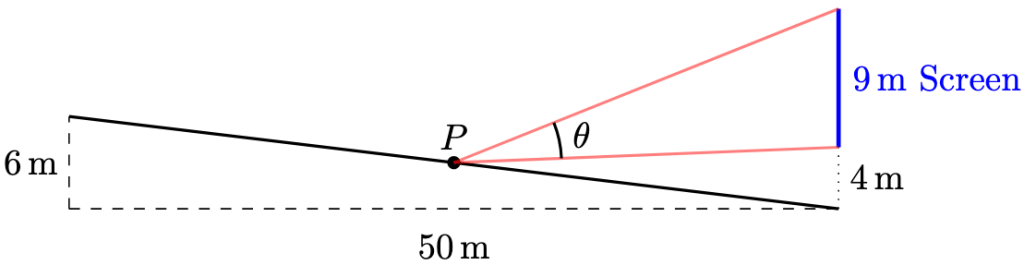
The permissible viewing area is $50\, \text{m}$ long with an incline of up to $6\, \text{m}$ . Determine the position that a movie-goer $P$ should sit in order to maximise his viewing angle $\theta$ , justifying your answer.

(Click for Solution)

Solution. Let $x$ denote the horizontal distance of the movie-goer from the screen. His height $y$ is then determined using similar triangles:

$\displaystyle \frac{y}{x} = \frac6{50} = \frac 3{25} \quad \Rightarrow \quad y = \frac{3}{25}x.$

By observation,

$\begin{aligned} \theta &= \tan^{-1} \left( \frac{13-y}{x} \right) - \tan^{-1} \left( \frac{4-y}{x} \right) \\ &= \tan^{-1} \left( \frac{13}{x} - \frac 3{25} \right) - \tan^{-1} \left( \frac{4}{x} - \frac 3{25} \right). \end{aligned}$

We remark that if $y > 4$ , then $4-y < 0$ and the formula still works. Differentiating with respect to $x$ ,

$\begin{aligned} \frac{\mathrm d\theta}{\mathrm dx} &= \frac{\mathrm d}{\mathrm dx}\tan^{-1} \left( \frac{13}{x} - \frac 3{25} \right) - \frac{\mathrm d}{\mathrm dx}\tan^{-1} \left( \frac{4}{x} - \frac 3{25} \right) \\ &= \frac{1}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2} \left( -\frac{13}{x^2} \right) - \frac{1}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} \left( -\frac{4}{x^2} \right) \\ &= -\frac 1{x^2} \left( \frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2} - \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} \right), \\ x^2 \frac{\mathrm d\theta}{\mathrm dx} &= \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} -\frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2}. \end{aligned}$

By the zero-derivative condition, if $\theta$ is maximised, then $\frac{\mathrm d\theta}{\mathrm dx} = 0$ :

$\begin{aligned}x^2 \cdot 0 &= \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} -\frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2}. \end{aligned}$

We need to (painfully) solve this equation:

$\begin{aligned} \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} &=\frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2} \\ 4 \cdot \left( 1 + \left( \frac{13}{x} - \frac 3{25} \right)^2 \right) &=13 \cdot \left( 1 + \left( \frac{4}{x} - \frac 3{25} \right)^2 \right) \\ 4 \cdot \left( 1 + \frac{169}{x^2} -\frac{78}{25x} + \frac{9}{625} \right) &=13 \cdot \left( 1 + \frac{16}{x^2} -\frac{24}{25x} + \frac{9}{625} \right) \\ 4 + \frac{676}{x^2} -\frac{312}{25x} + \frac{36}{625} &= 13 + \frac{208}{x^2} -\frac{312}{25x}+ \frac{117}{625} \\ \frac{468}{x^2} &= \frac{5706}{625} \\ x^2 &= \frac{16\, 250}{317} \\ x &= \sqrt{\frac{16\, 250}{317}} \approx 7.160\, \text{m}, \end{aligned}$

since $x > 0$ .

To apply second derivative test, we differentiate again:

$\begin{aligned} 2x \frac{\mathrm d\theta}{\mathrm dx} + x^2 \frac{\mathrm d^2\theta}{\mathrm dx^2} &= \frac{\mathrm d}{\mathrm dx} \left( \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} \right) -\frac{\mathrm d}{\mathrm dx} \left( \frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2} \right) \\ &= -\frac {4 \cdot 2\left( \frac{4}{x} - \frac 3{25} \right) \cdot -\frac{4}{x^2}}{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} + \frac {13 \cdot 2\left( \frac{13}{x} - \frac 3{25} \right) \cdot -\frac{13}{x^2}}{\left(1 + \left( \frac{13}{x} - \frac 3{25} \right)^2\right)^2} \\ &= \frac 2{x^2} \cdot \left( \frac {16 \cdot \left( \frac{4}{x} - \frac 3{25} \right) }{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} - \frac {169 \cdot \left( \frac{13}{x} - \frac 3{25} \right) }{\left(1 + \left( \frac{13}{x} - \frac 3{25} \right)^2\right)^2} \right).\end{aligned}$

When $\displaystyle \frac{\mathrm d\theta}{\mathrm dx} = 0$ , $\displaystyle \frac{4}{1 + \left( \frac{4}{x} - \frac 3{25} \right)^2} =\frac{13}{1 + \left( \frac{13}{x} - \frac 3{25} \right)^2}$ , so that

$\begin{aligned} 2x \cdot 0 + x^2 \frac{\mathrm d^2\theta}{\mathrm dx^2} &= \frac 2{x^2} \cdot \left( \frac {16 \cdot \left( \frac{4}{x} - \frac 3{25} \right) }{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} - \frac {16 \cdot \left( \frac{13}{x} - \frac 3{25} \right) }{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} \right) \\ &= \frac 2{x^2} \cdot \frac {16}{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} \cdot \left( \left( \frac{4}{x} - \frac 3{25} \right) - \left( \frac{13}{x} - \frac 3{25} \right) \right) \\ &= \frac 2{x^2} \cdot \frac {16}{\left(1 + \left( \frac{4}{x} - \frac 3{25} \right)^2\right)^2} \cdot -\frac 9x < 0, \end{aligned}$

so indeed $\theta$ will attain its maximum at $x = \sqrt{\frac{16\, 250}{317}}$ .

Question 3. Determine the smallest perimeter of a rectangle with area $1$ .

(Click for Solution)

Solution. Let $x, y$ denote the base and height of the rectangle respectively. Since $xy = 1$ implies $y = 1/x$ , the perimeter $P$ of the rectangle is given by

$\displaystyle P(x) = 2x + \frac 2x.$

Differentiating twice,

$\displaystyle P'(x) = 2 - \frac 2{x^2},\quad P''(x) = \frac 2{x^2} > 0.$

Solving $P'(x) = 0$ yields $x = 1$ so that $y = 1$ . Since $P''(1) > 0$ automatically, $x = 1$ yields a (local) minimum for $P$ . Hence, the rectangle has a minimum perimeter of $P(1) = 4$ , which corresponds to the rectangle being a square with base length $1$ .

Remark 1. The result remains true even if we consider rectangles of other areas; the rectangle with area $A$ whose perimeter is minimum must be a square with side length $\sqrt{A}$ .

Question 4. Given that $0 < x < 1$ , maximise $x^2(1-x)^3$ .

(Click for Solution)

Solution. Define $f(x) := x^2(1-x)^3$ . Differentiating twice,

$\begin{aligned} f'(x) &= 2x \cdot (1-x)^3 + x^2 \cdot 3(1-x)^2 \cdot (-1) \\ &= 2x \cdot (1-x)^3 - x^2 \cdot 3(1-x)^2 \\ &= x \cdot (1-x)^2 \cdot (2-5x), \\ f''(x) &= (1-x)^2\cdot (2-5x) + x \cdot 2(1-x) \cdot(-1) \cdot (2-5x) \\ &\phantom{==} + x \cdot (1-x)^2 \cdot (-5) \\ &= (1-x)^2\cdot (2-5x) - 2x(1-x) \cdot (2-5x) - 5x \cdot (1-x)^2. \end{aligned}$

Solving $f'(x) = 0$ , since $0 < x < 1$ , $2-5x = 0 \Rightarrow x = 2/5$ . Substituting into $f''$ ,

$f''(2/5) = 0 - 0 - 5 \cdot 2/5 \cdot (1-2/5)^2 < 0,$

so that $x = 2/5$ yields a local (global) maximum. Hence, $f$ has a maximum value of

$\displaystyle \left(\frac 25 \right)^2 \left(1 - \frac 25 \right)^3 = \frac{2^2 \cdot 3^3}{5^5} = \frac{108}{3125} = 0.03456.$

Remark 2. Using the same technique, we can prove that for any $0 < s < r$ and $s < x < r$ ,

$\displaystyle 0 < (x-s)^m (r-x)^n \leq m^m n^n \cdot \frac{(r-s)^{m+n}}{(m+n)^{m+n}}.$

with equality at $x = (rm+sn)/(m+n)$ . Setting $(s,r,m,n) = (0,1,2,3)$ yields Question 4.

Question 5. Given that $x > 0$ , find the value of $x$ that minimises $\displaystyle 6x^3 + 7/x^5$ .

(Click for Solution)

Solution. Define $f(x) := 6x^3 + 7/x^5 = 6x^3 + 7x^{-5}$ . Differentiating twice,

$\begin{aligned} f'(x) &= 18x^2 - 35x^{-6}, \\ f''(x) &= 36x + 210x^{-7} > 0. \end{aligned}$

Therefore, $f$ is minimised when $f'(x) = 0$ :

$\displaystyle 18x^2 - 35x^{-6} = 0 \quad \Rightarrow \quad x^8 = \frac{35}{18} \quad \Rightarrow \quad x = \sqrt[8]{ \frac{ 35 }{ 18 } },$

since $x > 0$ .

Remark 3. In general, the value of $x > 0$ that minimises $Ax^m + B/x^n$ is given by $x^{m+n} = (Bn)/(Am)$ .

—Joel Kindiak, 4 Sept 25, 1213H

KindiakMath