The Number Line

The number line helps us picture positive numbers, negative numbers, and even any point in between: we call these points real numbers, and represent them using the symbol $\mathbb R$ :

All of the familiar numbers belong to this line:

Natural numbers: $1, 2, 3, \dots$
Integers: $0, -1, -2, \dots$
Fractions: $\frac 12, \frac 13, \frac 23, \dots$
Negative fractions: $-\frac 12, -\frac 13, -\frac 23, \dots$

A number is called a rational number if it is either $0$ or a fraction or a negative fraction. Other numbers like

$\displaystyle \pi \approx 3 + \frac 1{10} + \frac 4{100} + \frac 2{1000} =: 3.142$

$\displaystyle \sqrt 2 \approx 1 + \frac 4{10} + \frac 1{100} + \frac 4{1000} =: 1.414$

are also real numbers that are not rational numbers:

$\pi$ calculates the length of the circumference of a circle with unit radius.
$\sqrt 2$ calculates the length of the diagonal of a unit square.

Using this point of view (pun intended) we can accept these rules for adding real numbers:

$\begin{aligned} a + b &= b + a, \\ a + (b + c) &= (a + b) + c, \\ a + 0 &= 0 + a = a, \\ a + (-a) &= (-a) + a = 0.\end{aligned}$

When positive, real numbers can also be used to describe areas.

Each positive real number length $b > 0$ matches a rectangle with base $b$ and height $1$ . If $b = 0$ , the rectangle becomes a line, which has $0$ area, giving the trivial equations

$b \times 1 = b,\quad 0 \times 1 = 0.$

We can therefore use different rectangles with the same area to recover many correct equations.

In particular, we obtain the following area properties for positive real numbers:

Commutativity: $b \times h = h \times b$
Multiplicative identity: $b \times 1 = 1 \times b = b$

Furthermore, we can use different rectangles with the same area to construct different real numbers. For example, we can use a square with area $4$ to construct the real number $2$ .

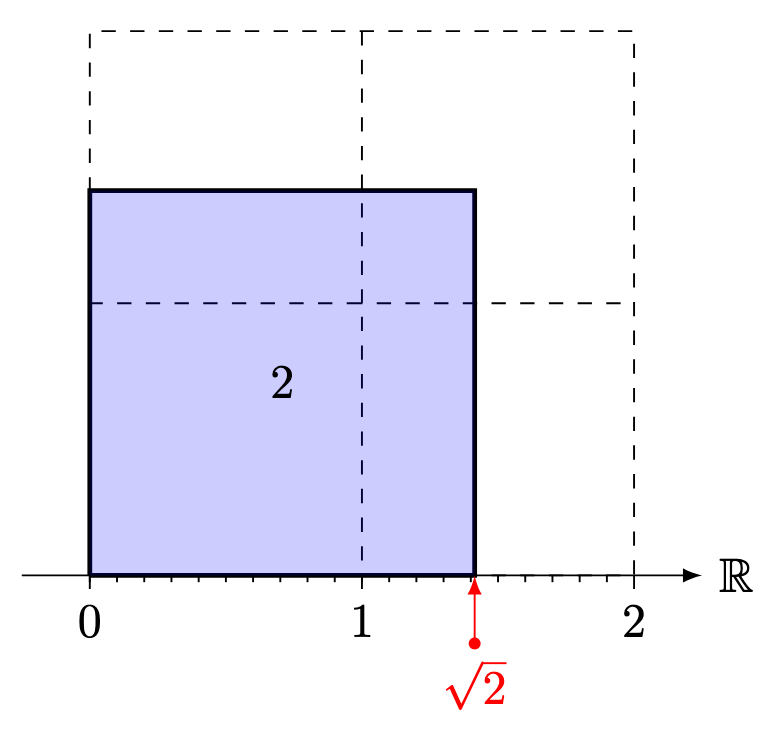
Likewise, we can use a square with area $2$ to construct the real number approximately equal to $1.414$ , which we represent using the symbol $\sqrt 2$ .

Remark 1. We will revisit this example when discussing geometry.

For this reason, we call this number the “square root” of $2$ : it is the root number, that when used to construct a square, produces a square with area $2$ . Replacing $2$ with any positive number $a$ ,

$(\sqrt a)^2 \equiv \sqrt a \times \sqrt a = a.$

Write $a \times b$ to mean the area of the rectangle with height $a$ and base $b$ :

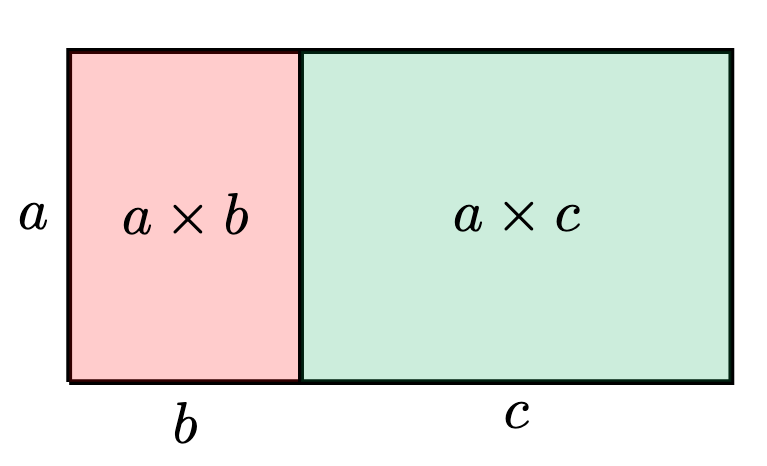
Since the two smaller rectangles combine into a larger rectangle with height $a$ and base $(b+c)$ , we recover the “rainbow method” to expand expressions (i.e. distributivity):

$\begin{aligned} a \times (b+c) &= (a \times b) + (a \times c), \\ (a + b) \times c &= (a \times c) + (b \times c), \end{aligned}$

where the second identity follows from the first:

$\begin{aligned}(a + b) \times c &= c \times (a + b) \\ &= (c \times a) + (c \times b) \\ &= (a \times c) + (b \times c). \end{aligned}$

Example 1. Evaluate $(a+b) \times (c + d)$ . In particular, evaluate $(a+b)^2$ .

Solution. By using the “rainbow method”,

$\begin{aligned}(a+b) \times (c + d) &= (a \times (c + d))+(b \times (c + d)) \\ &= (a \times c) + (a \times d)+(b \times c) + (b \times d). \end{aligned}$

Setting $a = c$ and $b = d$ ,

$\begin{aligned}(a+b)^2 &= (a+b) \times (a + b) \\ &= (a \times a) + (a \times b)+(b \times a) + (b \times b) \\ &= a^2 + (a \times b)+(a \times b) + b^2 \\ &= a^2 + 2 \times (a \times b) + b^2 .\end{aligned}$

Remark 2. Many students will sadly make the rookie mistake $(a+b)^2 = a^2 + b^2$ .

Example 2. Explain why it is not true in general that $\displaystyle \sqrt{a+b} = \sqrt{a} + \sqrt{b}$ .

Solution. Consider the case $a = 1$ and $b = 1$ . Then

$\displaystyle \sqrt{a+b} = \sqrt{1+1} = \sqrt 2 \approx 1.414 \neq 2 = 1 + 1 = \sqrt a + \sqrt b.$

We call this violation of a proposed general pattern a counterexample.

We can do better. Consider the rectangle below with base $b > 0$ , height $h > 0$ , and area $1$ .

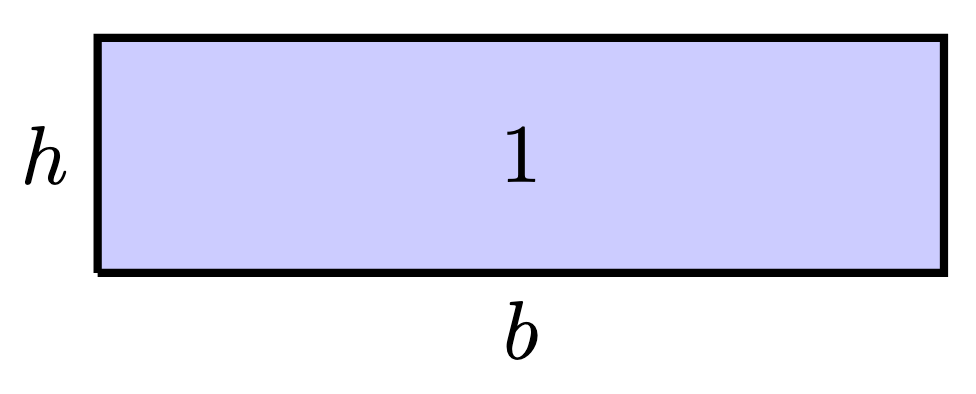
Since there is only one rectangle with base $b$ and area $1$ , there is exactly one positive number $h$ such that

$b \times h = 1.$

We define $\displaystyle \frac 1b := h$ , and inverse property:

$\displaystyle b \times \frac 1b = \frac 1b \times b = 1.$

Hence, we define real number division by

$\displaystyle \frac nd := n \times \frac 1d,\quad d \neq 0.$

Remark 3. If $b = 0$ , then no matter what height $h$ we have, the area of the corresponding rectangle will be $b \times h = 0 \times h = 0$ . Hence, the quantity $\displaystyle \frac 10$ is undefined. In other words: division by $0$ is illegal.

Example 3. Given $c \neq 0$ , show that $\displaystyle \frac ac +\frac bc = \frac {a+b}{c}$ .

Proof. Using real number division,

$\begin{aligned} \frac ac +\frac bc &= a \times \frac 1c + b \times \frac 1c \\ &= (a + b) \times \frac 1c \\ &= \frac{a+b}{c}.\end{aligned}$

If we want to multiply many times, we can bump things up by one dimension. Consider the volume of a cuboid with base $b$ , width $w$ , and height $h$ .

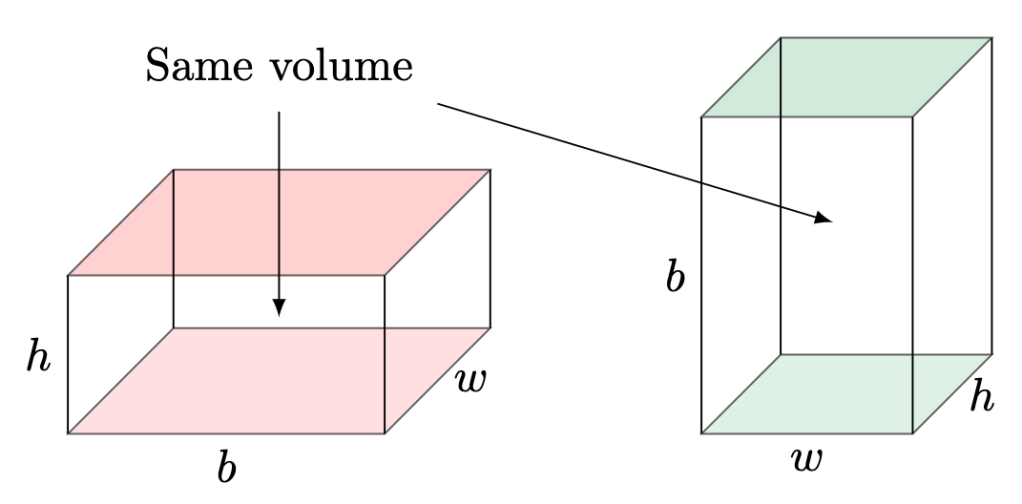
Since both cuboids have the same volume, we can multiply in either order (i.e. associativity):

$\displaystyle (b \times w) \times h = b \times (w \times h).$

Hence, we can define three-way multiplication by

$a \times b \times c := a \times (b \times c)$

without confusion. For products of even more numbers, though we would find it difficult to imagine objects beyond volume, we don’t need to worry:

$\begin{aligned} a \times (b \times c \times d) &= a \times ((b \times c) \times d) \\ &= (a \times (b \times c)) \times d \\ &= (a \times b \times c) \times d. \end{aligned}$

Example 4. Given $b, d \neq 0$ , show that $\displaystyle (b \times d) \times \left( \frac 1b \times \frac 1d \right) = 1$ . In particular,

$\displaystyle \frac 1{b \times d} = \frac 1b \times \frac 1d.$

Proof. Since we can multiply in any order of “brackets”,

$\begin{aligned}(b \times d) \times \left( \frac 1b \times \frac 1d \right) &= b \times d \times \frac 1b \times \frac 1d \\ &= b \times \frac 1b \times d \times \frac 1d \\ &= 1 \times 1 = 1.\end{aligned}$

Corollary 1. Given $b, d \neq 0$ ,

$\displaystyle \frac ab \times \frac cd = \frac{a \times c}{b \times d},\quad \frac ab + \frac cd = \frac{(a \times d) + (b \times c)}{b \times d}.$

Proof. Using Example 4,

$\begin{aligned} \frac ab \times \frac cd &= \left( a \times \frac 1b \right) \times \left( c \times \frac 1d \right) \\ &= (a \times c) \times \left( \frac 1b \times \frac 1d \right) \\ &= (a \times c) \times \frac 1{b \times d} = \frac{a \times c}{b \times d}. \end{aligned}$

To add two fractions, use Example 3:

$\begin{aligned} \frac ab + \frac cd &= \left(\frac ab \times 1 \right) + \left(\frac cd \times 1 \right) \\ &= \left(\frac ab \times \frac dd \right) + \left(\frac cd \times \frac bb \right) \\ &= \frac{a \times d}{b \times d} + \frac{c \times b}{d \times b} \\ &= \frac{a \times d}{b \times d} + \frac{b \times c}{b \times d} \\ &= \frac{(a \times d) + (b \times c)}{b \times d}. \end{aligned}$

Remark 4. By the principle in Remark 3, you might think that the number $\displaystyle \frac 1{-2}$ is also undefined. After all, how can a rectangle have negative base length? That is because we are using areas as an analogy to describe real number calculations. Nevertheless, the quantity $\displaystyle \frac{1}{-2}$ is still well defined; indeed, using Corollary 1,

$\displaystyle \frac{1}{-2} = \frac{(-1) \times (-1)}{(-1) \times 2} = \frac{-1}{-1} \times \frac{-1}{2} = \frac{-1}{2} = - \frac 1{2},$

and $\frac 12$ is a clearly well-defined positive fraction, so that $-\frac 12$ is a perfectly well-defined rational number. However, trying to define $\displaystyle \frac 10$ will create problems:

$\displaystyle \frac 10 = \frac{\frac 12 \times 2}{\frac 12 \times 0} = \frac {\frac 12 }{\frac 12 } \times \frac 20 = \frac 20 = 2 \times \frac 10$

implies that

$\displaystyle \frac 10 = 0 \quad \Rightarrow \quad 0 \times 0 = 1,$

which is absurd. Therefore, $\displaystyle \frac 10$ remains undefined:

Division by zero is (generally) mathematically illegal.

Corollary 2. Given $b, d \neq 0$ ,

$\displaystyle \frac ab - \frac cd = \frac{(a \times d) - (b \times c)}{b \times d}.$

Proof. Recall that $-r = (-1) \times r$ :

$\begin{aligned} - \frac{c}{d} &= (-1) \times \frac{c}{d} = \frac{(-1) \times c}{d} = \frac{-c}{d}. \end{aligned}$

Recall the definition

$s - t = s + (-t) = s + ((-1) \times t).$

Hence, use Corollary 1 to deduce that

$\begin{aligned} \frac ab - \frac cd &= \frac ab + \left( - \frac cd \right) \\ &= \frac ab + \frac {(-1) \times c}d \\ &= \frac{(a \times d) + (b \times (-1) \times c)}{b \times d} \\ &= \frac{(a \times d) + ((-1) \times (b \times c))}{b \times d} \\ &= \frac{(a \times d) - (b \times c)}{b \times d}. \end{aligned}$

Numbers mean nothing unless we can perform meaningful calculations with them. To add two fractions, we first find their (lowest) common denominator, then add them normally.

Example 5. Evaluate $\displaystyle \frac 23 + \frac 45$ without a calculator.

Solution. By using the common denominator $\mathrm{LCM}(3,5) = 3 \times 5= 15$ and Corollary 1,

$\begin{aligned} \frac 23 + \frac 45 &= \frac{(2 \times 5) + (4 \times 3)}{3 \times 5} = \frac{10 + 12}{15} = \frac{22}{15}. \end{aligned}$

Example 6. Evaluate $\displaystyle \frac 67 - \frac 89$ without a calculator.

Solution. Following Example 5 but instead using $\mathrm{LCM}(7,9) = 7 \times 9 = 63$ and Corollary 2,

$\begin{aligned} \frac 67 - \frac 89 &= \frac{(6 \times 9) - (7 \times 8)}{7 \times 9} = \frac{54 - 56}{63} = \frac{-2}{63} = -\frac 2{63}. \end{aligned}$

Example 7. Explain why it is not always true that $\displaystyle \frac 1{a+b} = \frac 1{a} + \frac 1{b}$ .

Solution. Consider the case $a = 1$ and $b = 1$ . Then

$\displaystyle \frac 1{a+b} = \frac 1{1+1} = \frac 12 \neq 2 = 1 + 1 = \frac 1a + \frac 1b.$

Oddly enough, we have derived the important main ideas for calculating using real numbers, so we can extend these ideas to discuss basic algebraic manipulations in the next post.

What remains are some technical remarks about our discussions.

Remark 5. It turns out that for any non-zero real number $a, b$ ,

$\displaystyle \frac 1{a+b} = \frac 1{a} + \frac 1{b}$

is always not true (i.e. false)! Similarly, if $a > 0$ and $b > 0$ , then the statement

$\sqrt{a+b} = \sqrt a + \sqrt b$

is always false.

Remark 6. We have built the basics of real number calculations, and since we will use the letters $x$ and $y$ soon, it gets very messy to write $x \times y$ . To simplify our work, we write $xy := x \times y$ , so that the “rainbow method” looks like

$a(b+c) = ab + ac.$

In particular, Example 1 looks like the following:

$(a+b)^2 = a^2 + 2ab + b^2.$

Sometimes, we use a dot to to clarify that we are doing multiplication:

$x\cdot y \equiv xy \equiv x \times y.$

Hence, we have the identities

$a \cdot (b + c) = a \cdot b + a \cdot c,\quad a^2 = a \cdot a.$

Without brackets, we will always multiply before adding:

$a \cdot b + a \cdot c \equiv (a \cdot b) + (a \cdot c),$

leading to the usual PEMDAS rule:

parentheses (or brackets),
exponents (e.g. $a^2$ ),
multiplication / division,
and finally addition / subtraction.

In fact, division is defined using multiplication:

$\displaystyle a \div b \equiv \frac ab := a \times \frac 1b,\quad b \neq 0.$

Likewise, subtraction is defined using addition:

$\displaystyle a - b := a + (-b).$

Remark 7. To properly construct the real numbers, beyond the rectangle-area picture, takes a lot more effort. We first need to define the rational numbers, then the real numbers, and finally for completeness, the complex numbers.

—Joel Kindiak, 23 Sept 25, 1556H

KindiakMath

The Number Line

Leave a comment Cancel reply

The Number Line

Share this:

Leave a comment Cancel reply