Pythagoras’ Trophy

Pythagoras’ theorem is the most important idea in geometry, all of mathematics even. But before discussing it, let’s ask a simple question.

Given a unit length $1$ , and a positive number $R$ , how can we construct $\sqrt R$ ?

Recall that $\sqrt R = s$ means that $s^2 = R$ . We can achieve this construction goal using Pythagoras’ theorem.

(A proper construction, as with many other geometric ideas, relies on real analysis.)

Theorem 1 (Pythagoras’ Theorem). Given a right-angled triangle below,

$a^2 + b^2 = c^2.$

We call the longest side with length $c$ the hypotenuse of the triangle.

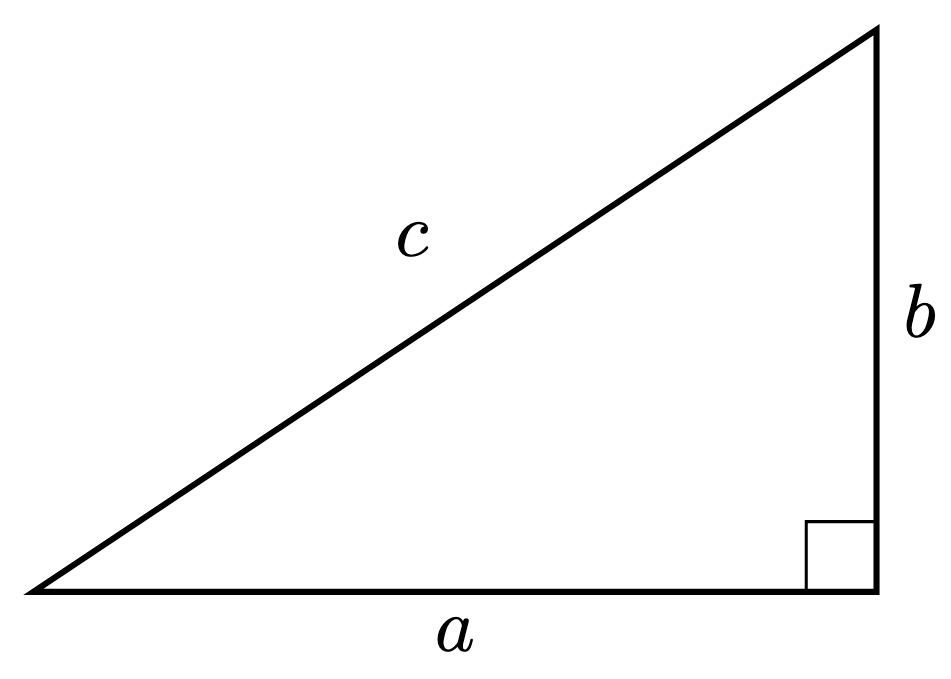
If $a,b,c$ are positive integers, we call $(a,b,c)$ a Pythagorean triple. The most famous such example would be the $3$ – $4$ – $5$ triple:

$3^2 + 4^2 = 25 = 5^2.$

Proof. Draw three extra identical triangles, so that we get a large square with side length $a + b$ .

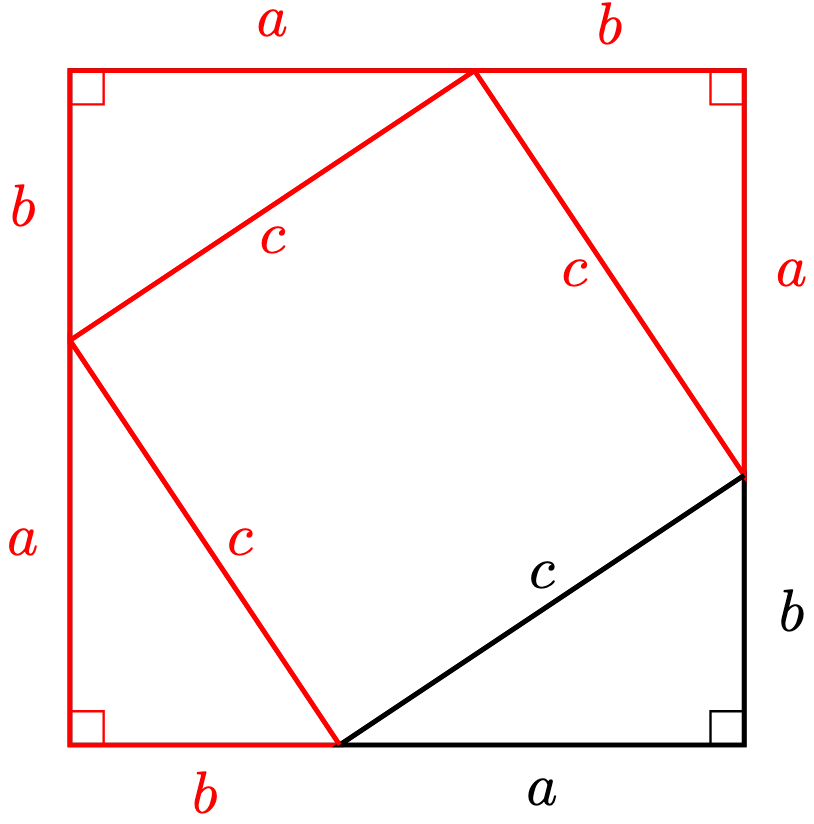
We claim that the slanted four-sided shape (i.e. a quadrilateral) in the middle is indeed a square.

Since the right-angled triangles are identical, we take two adjacent triangles and label their angles as follows.

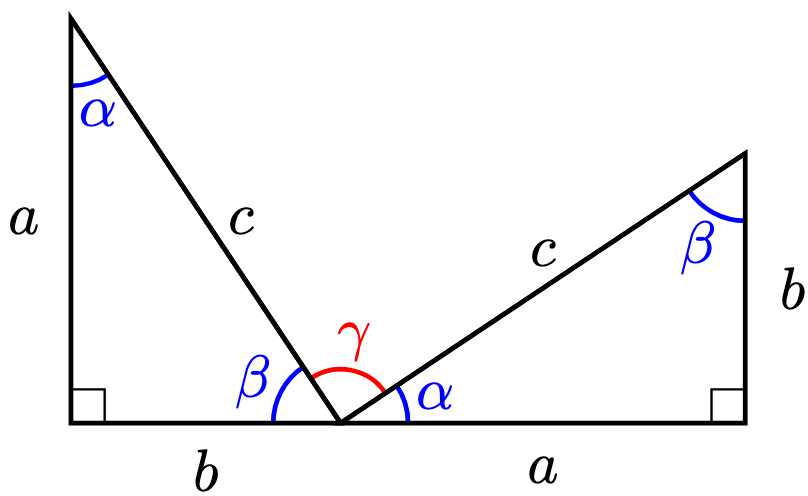
We want to prove that $\gamma = 90^\circ$ . Since the angles in the centre are non-overlapping adjacent angles on a straight line,

$\alpha + \gamma + \beta = 180^\circ.$

On the other hand, since the angles in a triangle sum to $180^\circ$ ,

$\alpha + \beta + 90^\circ = 180^\circ.$

Therefore, using usual calculations,

$\begin{aligned} \alpha + \gamma + \beta &= \alpha + \beta + 90^\circ\\ \gamma &= 90^\circ. \end{aligned}$

Since the hypotenuses are all equal, we know that the quadrilateral has four equal sides. Hence, we have a square in the middle whose area is $c^2$ , so that

$\begin{aligned} (a+b)^2 &= 4 \cdot \frac 12 \cdot a \cdot b + c^2 \\ a^2 + 2ab + b^2 &= 2ab + c^2 \\ a^2 + b^2 &= c^2. \end{aligned}$

There are many applications of Pythagoras theorem that, in my humble opinion, are not worth discussing outside a tuition class. Yet, Pythagoras’ theorem can resolve for us a simple yet non-trivial question: what is a circle?

You might say, “a circle is a non-straight bendy or curvy line that closes in on itself”. This formulation is valid when formalised in the language of algebraic topology and homology theory.

Let’s keep things simple for now.

Definition 1. A circle with centre $P$ and radius $r$ is the unique set of points whose distance from $P$ is $r$ . In particular, we define the unit circle to be a circle with centre $P$ and radius $r$ .

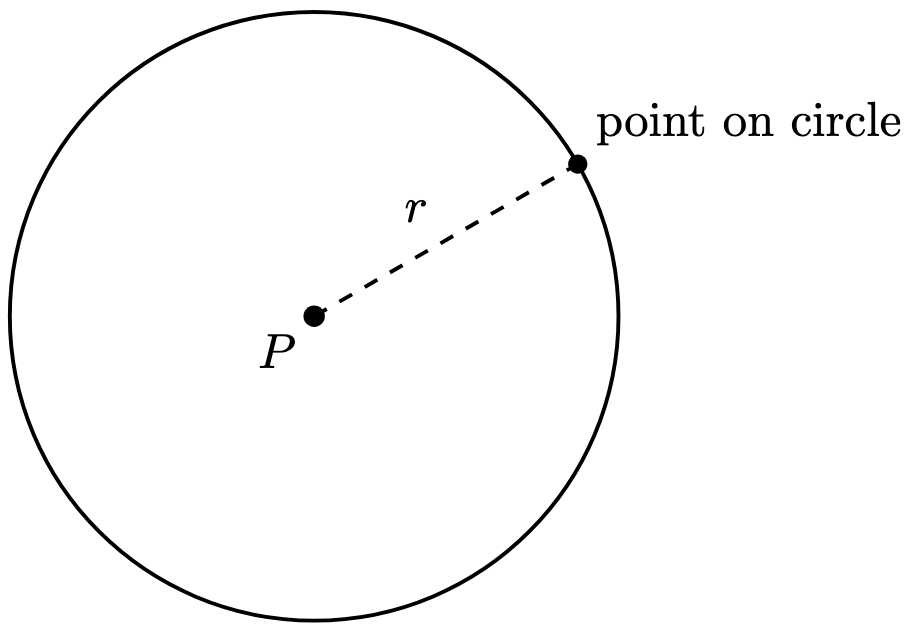
There is one problem with this definition: how do we calculate the distance between two points without requiring any additional measurement?

Lemma 1. The distance $d_{PQ}$ between two points $P(x_1,y_1)$ and $Q(x_2,y_2)$ is given by

$\displaystyle d_{PQ} := \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$

Proof Sketch. Suppose the special case $x_1 < x_2$ and $y_1 < y_2$ .

Construct the right-angled triangle below.

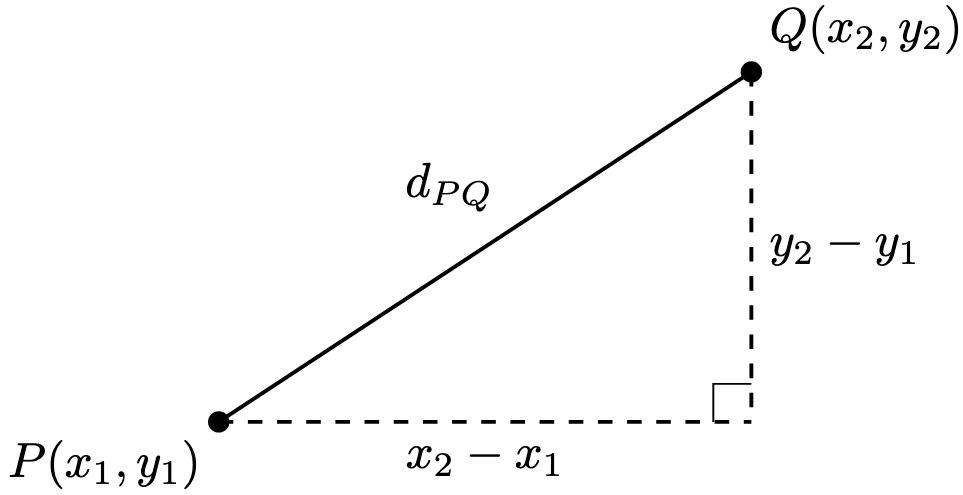
Then the hypotenuse of this right-angled triangle has length $d_{PQ}$ . Applying Pythagoras’ theorem,

$d_{PQ}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2.$

Taking square roots gives the desired result.

The other cases involving $x_1 \geq x_2$ or $y_1 \geq y_2$ are left as an exerice to the reader.

Call any collection of points a graph.

Theorem 2. The graph $C$ is a circle with centre $(h,k)$ and radius $r$ if and only if it is defined by the equation

$(x-h)^2 + (y-k)^2 = r^2.$

In particular, the unit circle has equation $x^2 + y^2 = 1$ .

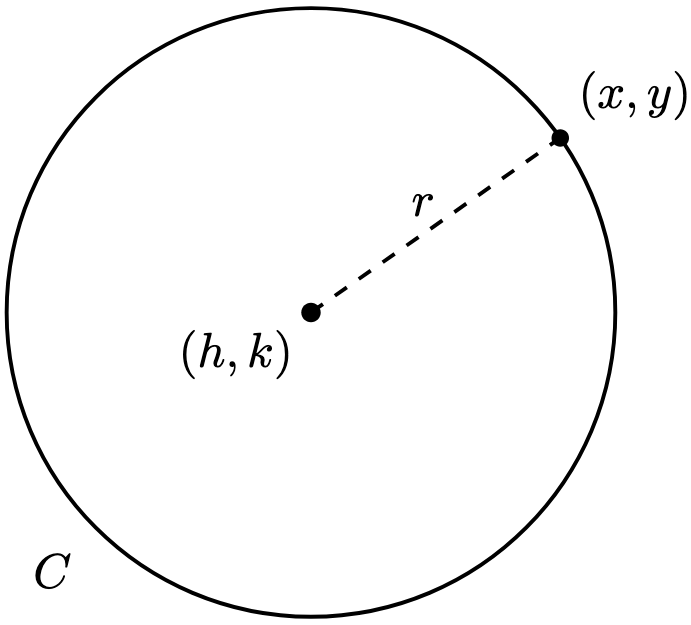
Proof. By definition, a point $(x,y)$ belongs to the circle if and only if its distance to $(h,k)$ is $r$ . By Lemma 1, this condition holds if and only if

$\sqrt{(x-h)^2 + (y-k)^2} = r.$

Squaring on both sides, since $r > 0$ , we obtain the equation

$(x-h)^2 + (y-k)^2 = r^2,$

as required.

Once we can properly discuss circles, all sorts of interesting mathematics arise. But we will revisit circles later on.

For now, let’s answer the question we opened with: constructing $\sqrt R$ geometrically.

Theorem 3. Fix $R > 0$ . Define $r := (R+1)/2$ . Define the line $L$ by $x = r-1$ and the circle $C$ to be a circle with centre $O(0,0)$ and radius $r$ .

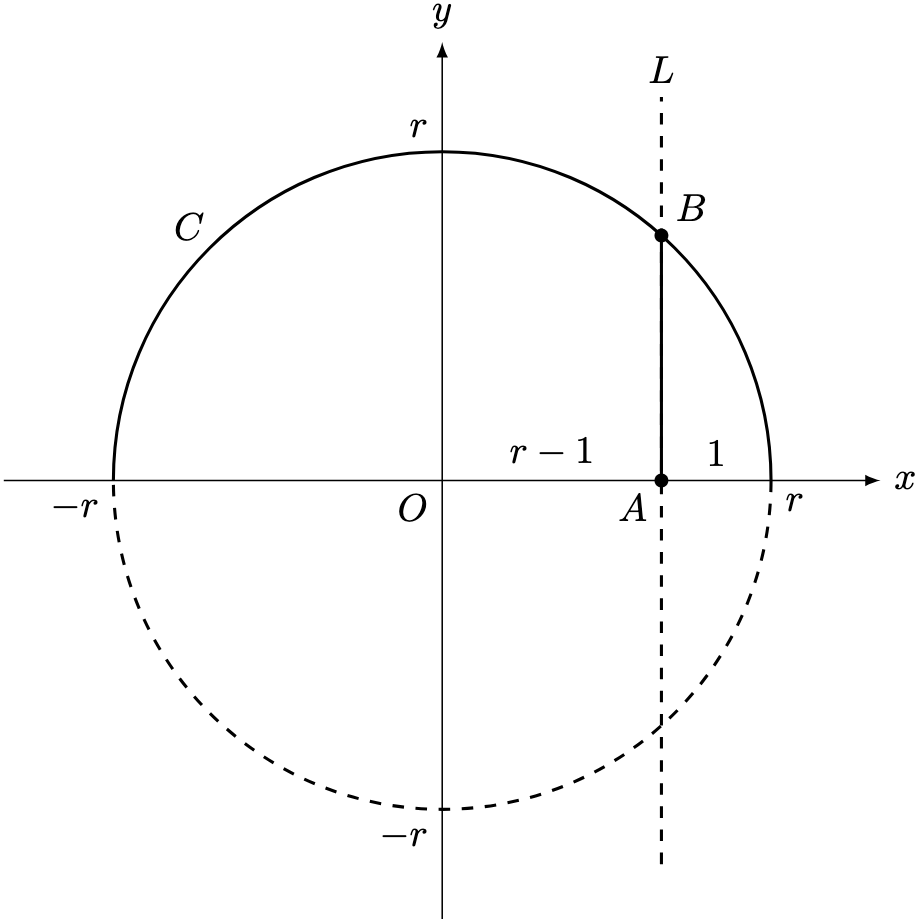
Then $AB = \sqrt {R}$ .

Proof. By Theorem 2, $C$ has equation

$x^2 + y^2 = r^2.$

To obtain the coordinates of $B$ , we need to solve the equations

$x = r-1\quad \text{and}\quad x^2 + y^2 = r^2,$

and require $y > 0$ . We will use the substitution method as follows—substitute the equation $x = r-1$ into the circle equation:

$\begin{aligned} (r-1)^2 + y^2 &= r^2 \\ (r^2 - 2r + 1) + y^2 &= r^2 \\ - 2r + 1 + y^2 &= 0 \\ -(R+1) + 1 + y^2 &= 0 \\ -R + y^2 &= 0 \\ y^2 &= R. \end{aligned}$

Since $y > 0$ , by definition, $y = \sqrt{R}$ . Since $A(r-1, 0)$ and $B(r-1, \sqrt R)$ , by Lemma 1,

$\begin{aligned} AB &= \sqrt{((r-1) - (r-1))^2 + (\sqrt R - 0)^2} = \sqrt{0 + R} = \sqrt{R}. \end{aligned}$

There is a lot more to circles than this one example, but for now, we return to triangles in the next post. In particular, the isosceles triangle will be a central tool in our geometric expedition.

—Joel Kindiak, 10 Oct 25, 2026H

KindiakMath

Pythagoras’ Trophy

Leave a comment Cancel reply

Pythagoras’ Trophy

Share this:

Leave a comment Cancel reply