Circular Magic

Recall that a circle with centre $C$ and radius $r$ is simply the set of points whose distance from $C$ is $r$ .

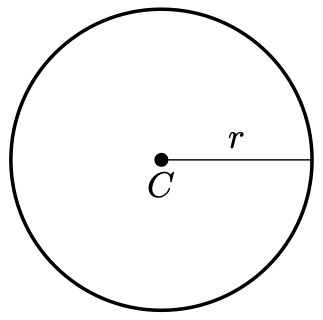
The equidistant property is vital and the source of many seemingly magical circle properties—and the isosceles triangle is our intermediate tool of choice.

Definition 1. For any two distinct $A,B$ on a circle, we call $AB$ a chord, and the regions that it divides the circle into its segments.

The segment with smaller area is called the minor segment, and the segment with larger area is called the major segment.

Theorem 1. Let $A,B,D$ be points on a circle with centre $C$ . We call $\angle ADB$ the angle subtended by the chord $AB$ .

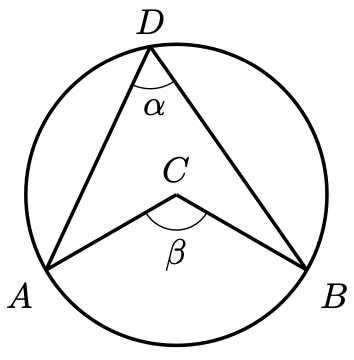
Then $\beta = 2\alpha$ . That is, the angle at the centre of the circle equals two times the corresponding angle at its circumference. By “corresponding” we mean that $C,D$ lie in the same segment.

Proof. Connect $CD$ as follows and extend $CD$ to the end of the other circle (i.e. turn it into a diameter).

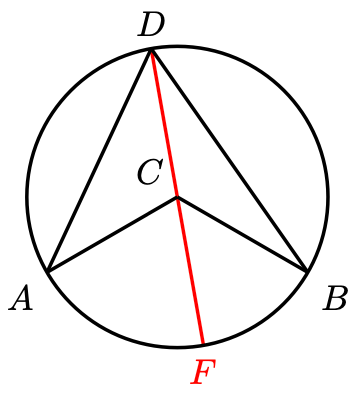
Observe that as radii (plural for radius) of the same circle, $CA = CD = CB$ . Hence, the triangles $\Delta CAD$ and $\Delta CBD$ are isosceles, and their respective base angles equal each other:

$\angle CAD = \angle CDA,\quad \angle CBD = \angle CDB.$

Since the external angle of the triangle $\Delta ACD$ equals the sum of the corresponding opposite interior angles,

$\angle ACF = \angle CDA + \angle CAD = \angle CDA + \angle CDA = 2 \cdot \angle CDA.$

Similarly, $\angle BCF = 2 \cdot \angle CDB$ . Therefore,

$\begin{aligned} \beta &= \angle ACB \\ &= \angle ACF + \angle BCF \\ &= 2 \cdot \angle CDA + 2 \cdot \angle CDB \\ &= 2 \cdot (\angle CDA + \angle CDB) \\ &= 2 \cdot \angle ADB = 2\alpha. \end{aligned}$

Remark 1. If $\alpha$ is obtuse, then the argument still holds and $\beta > 180^\circ$ . In this case, we say that $\beta$ is reflex.

Corollary 1 (Thale’s Theorem). Consider the points $A,B,C$ on the circle below.

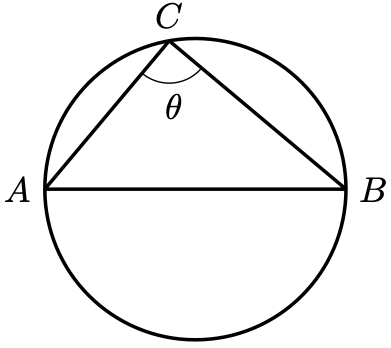
Then $\theta = 90^\circ$ if and only if $AB$ is a diameter of the circle.

Proof. Denote the centre of the circle by $D$ .

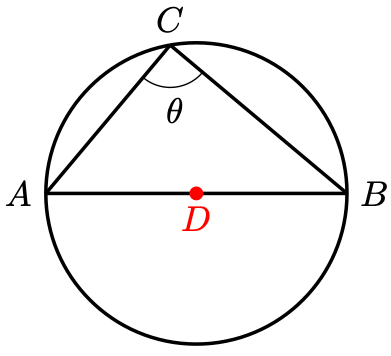
By Theorem 1, $\angle ADB = 2\theta$ . Hence,

$\theta = 90^\circ\quad \iff \quad \angle ADB = 180^\circ,$

which holds if and only if $D$ lies on $AB$ , and that holds if and only if $AB$ is a diameter.

Corollary 2. Consider the points $A,B,C,D$ on the circle below.

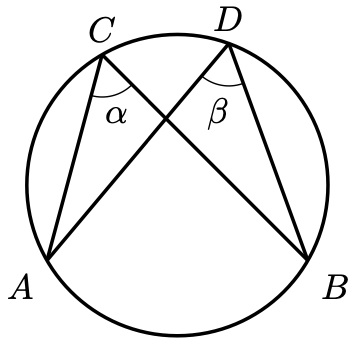
Then $\alpha = \beta$ . That is, angles subtended by the same chord equal each other.

Proof. Denote the centre of the circle by $F$ .

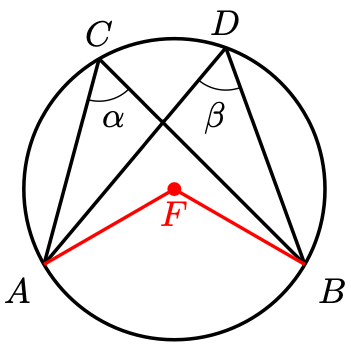
Applying Theorem 1 twice,

$\angle AFB = 2\alpha,\quad \angle AFB = 2\beta.$

Therefore, $2\alpha = 2\beta \Rightarrow \alpha = \beta$ .

Corollary 3. Consider the points $A,B,C,D$ on the circle below.

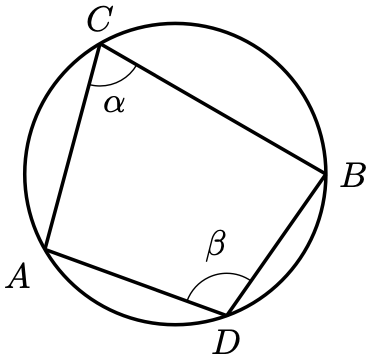
Then $\alpha + \beta = 180^\circ$ . That is, angles in opposite segments sum to $180^\circ$ (i.e. are supplementary).

Proof. Denote the centre of the circle by $F$ .

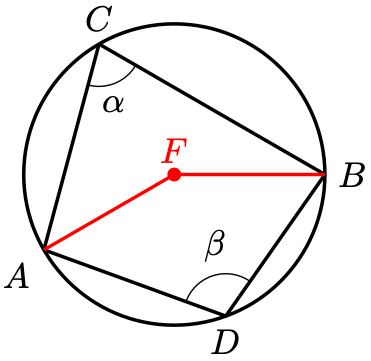
By Theorem 1, $\angle AFB = 2\alpha$ . By Theorem 1 again, the reflex angle of $\angle AFB$ equals $2\beta$ . Since angles at a point sum to $360^\circ$ ,

$\begin{aligned} 2 \alpha + 2\beta &= 360^\circ \\ \alpha + \beta &= 180^\circ. \end{aligned}$

While we have derived many useful angle properties pertaining circles, the chords themselves are worth just as much attention, and their proofs aren’t even too difficult!

Definition 2. The midpoint of a line segment $AB$ is the point $C$ such that $AC = CB$ .

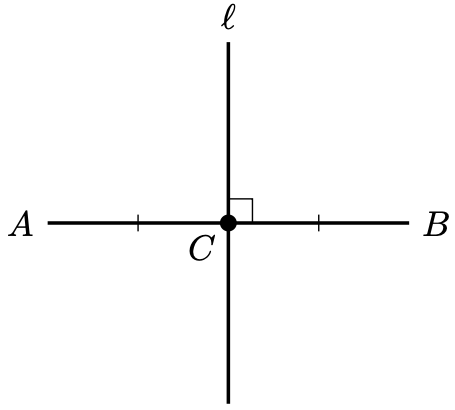
Call the line $\ell$ the perpendicular bisector of $AB$ if $\ell \perp AB$ and it intersects $AB$ at the midpoint of $AB$ .

Theorem 2. Consider the points $A,B$ on the circle with centre $C$ below.

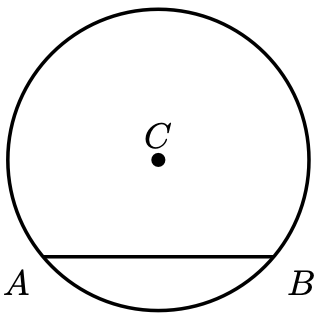
Then the perpendicular bisector of $AB$ will always intersect $C$ .

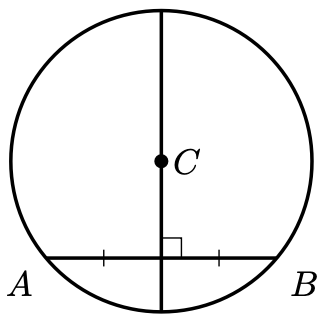
Proof. Construct the edges $AC$ and $BC$ for visibility and construct the altitude from $C$ to $AB$ .

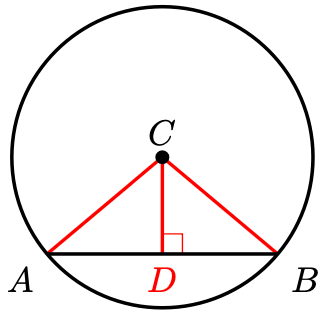
Since $AC, BC$ are radii of the same circle, $AC = BC$ . Since adjacent angles on a straight line are supplmenetary, $\angle ADC = \angle BDC = 90^\circ$ . Since $CD$ is a common side, by the RHS Criterion, $\Delta ACD \equiv \Delta BCD$ .

In particular, $AD = BD$ , which means that $CD$ lies on the perpendicular bisector of $AB$ . Therefore, $C$ lies on the perpendicular bisector of $AB$ , as required.

Definition 3. Define the distance from a point $P$ to a line $\ell$ to be the shortest distance $d$ between the point and any point on the line.

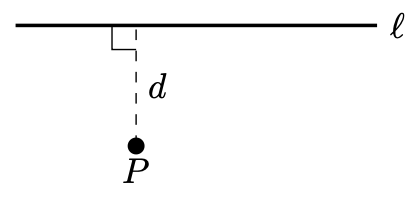
By Pythagoras’ theorem, this distance must be the length of the altitude from $P$ , perpendicular to $\ell$ .

Theorem 3. Consider the points $A,B,F,G$ on the circle with centre $C$ below.

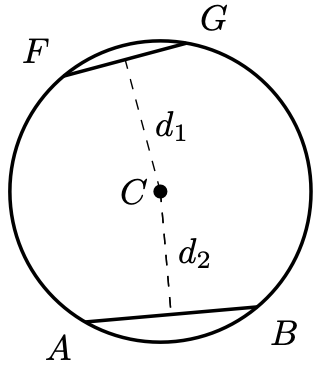
Then $d_1 = d_2$ if and only if $AB = FG$ .

Proof. Construct the edges $AC,BC,FC,GC$ for visibility.

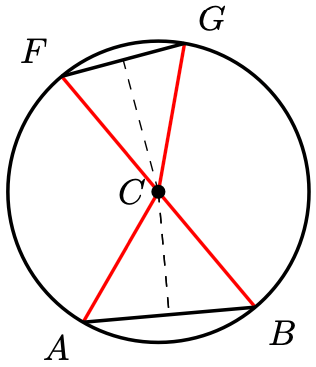
Since $AC,BC,FC,GC$ are radii of the same circle, $AC = BC = FC = GC$ . By various triangle congruence criteria (left as an exercise),

$d_1 = d_2 \quad \iff \quad \Delta ABC \equiv \Delta FGC \quad \iff \quad AB = FG.$

There are several more properties needed to properly conclude our discussion on circles, but we will relegate them as exercises in proving techniques.

For now, we need to consider other kinds of shapes, such as four-sided shapes, known as quadrilaterals, as well as more general $n$ -sided shapes called polygons. We don’t need any new machinery—whatever we have discussed so far suffices to establish these results, which we will explore next time.

—Joel Kindiak, 15 Oct 25, 2242H

KindiakMath

Circular Magic

Leave a comment Cancel reply

Circular Magic

Share this:

Leave a comment Cancel reply