KindiakMath

Category: Exercises

H2 Math 2025 Suggested Answers (Paper 2)
Questions have not been uploaded due to copyright reasons. Do comment if you spot any errors.

Section A: Pure Mathematics [40 marks]

Question 1. System of Linear Equations

Solution. (a) Using the question,

$\displaystyle \left\{ \begin{matrix} 8c + 11t + 5b = 114, \\ 5c + 14t + 7b = 112, \\ 9c + 9t + 4b = 110. \end{matrix} \right.$

Solving the system of linear equations, $c = 7, t= 3, b = 5$ .

(b) By the question, Sam scored $113$ points. Let $x,y,z$ denote the number of car, train, and boat tokens respectively that Sam has. Hence,

$\displaystyle 7x + 3y + 5z = 113.$

Furthermore, we are given that $x \geq 6, y \geq 6, z \geq 6$ , so that

$\displaystyle 7x + 3y + 5z \geq 90.$

Since the sum is $113$ , at least one of $x,y,z$ must be odd. Furthermore, by fixing $y = z = 6$ for simplicity, we must have $7x \leq 65 \Rightarrow x \leq 9$ . Similarly, $y \leq 13$ and $z \leq 10$ .

By trial-and-error, $x = 6$ , $y = 7$ , $z = 10$ works. Since there is only one solution, Sam had $6$ car tokens, $7$ train tokens, and $10$ boat tokens.

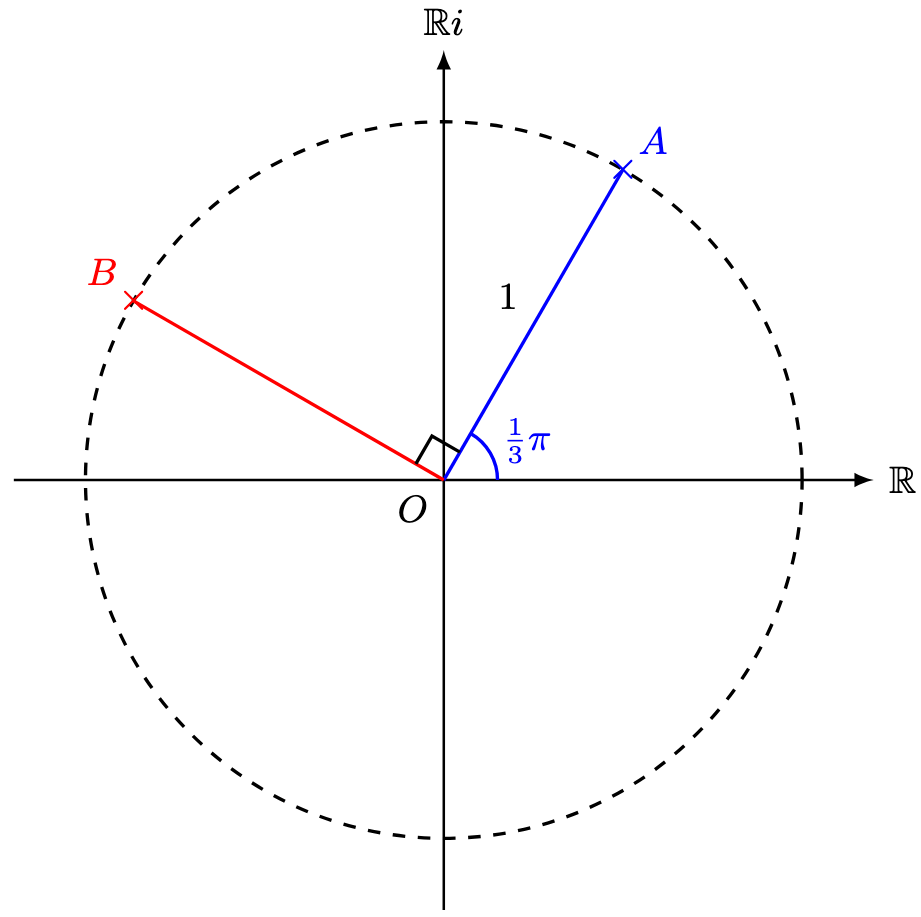
Question 2. Vectors

Solution. (a) Firstly,

$\overrightarrow{PQ} = \begin{bmatrix} 1 \\ 6 \\ 6 \end{bmatrix} - \begin{bmatrix} -2 \\ 3 \\ 0 \end{bmatrix} = \begin{bmatrix} 3 \\ 3 \\ 6 \end{bmatrix}.$

Since $\overrightarrow{QR} = \frac 43 \overrightarrow{PQ}$ and $P,Q,R$ are collinear, we have

$\begin{aligned} \overrightarrow{PR} &= \overrightarrow{PQ} + \overrightarrow{QR} \\ &= \overrightarrow{PQ} + {\textstyle \frac 43} \overrightarrow{PQ} \\ &= {\textstyle \frac 73} \overrightarrow{PQ} = {\textstyle \frac 73} \begin{bmatrix} 3 \\ 3 \\ 6 \end{bmatrix} = \begin{bmatrix} 7 \\ 7 \\ 14 \end{bmatrix}.\end{aligned}$

Hence,

$\overrightarrow{OR} = \overrightarrow{OP} + \overrightarrow{PR} = \begin{bmatrix} -2 \\ 3 \\ 0 \end{bmatrix} + \begin{bmatrix} 7 \\ 7 \\ 14 \end{bmatrix} = \begin{bmatrix} 5 \\ 10 \\ 14 \end{bmatrix}.$

(b) Firstly,

$\overrightarrow{ SQ } = \begin{bmatrix} 1\\ 6 \\ 6 \end{bmatrix} - \begin{bmatrix} -1 \\ -2 \\ c \end{bmatrix} .$

Since $\overrightarrow{ SQ } \perp \overrightarrow{ PQ }$ :

$\begin{aligned} \left( \begin{bmatrix} 1\\ 6 \\ 6 \end{bmatrix} - \begin{bmatrix} -1 \\ -2 \\ c \end{bmatrix} \right) \cdot \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} &= 0 \\ (1+6+12) - (-1-2+2c) &= 0 \\ 19 - (2c-3) &= 0 \\ c &= 11 .\end{aligned}$

(c) Hence,

$\overrightarrow{ PS } = \begin{bmatrix} -1 \\ -2 \\ 11 \end{bmatrix} - \begin{bmatrix} -2 \\ 3 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ -5 \\ 11 \end{bmatrix}.$

Therefore the required angle $\theta$ is given by

$\begin{aligned} \begin{bmatrix} 1 \\ -5 \\ 11 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} &= \left\| \begin{bmatrix} - 1 \\ -5 \\ 11 \end{bmatrix} \right\| \left\| \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} \right\| \cos \theta \\ 18 &= \sqrt{147} \sqrt{6} \cos \theta \\ \cos \theta &= \frac{18}{\sqrt{147} \sqrt 6}\\ \theta &\approx 52.7^\circ. \end{aligned}$

Question 3. Differential Equations

Solution. (a) By the method of separable variables,

$\begin{aligned} \int y^{-2}\, \mathrm dy &= \int \sin 3x\, \mathrm dx \\ \frac{y^{-1}}{-1} &= -\frac 13 \cos 3x + C \\ \frac 1y &= \frac 13 \cos 3x - C \\ y &= \frac{1}{-C + \frac 13 \cos 3x}. \end{aligned}$

Since the initial condition is $y(\pi) = 1$ ,

$\displaystyle 1 = \frac{1}{-C + \frac 13 \cos 3\pi} \quad \Rightarrow \quad C = -\frac 43 .$

Therefore, $\displaystyle y = \frac{1}{\frac 43 + \frac 13 \cos 3x} = \frac 3{4 + \cos 3x}$ , where $A = 3, B= 4$ .

(b) (i) By the graph $c = 3/5, 1$ (these values correspond with $\cos(x) = \pm 1$ ).

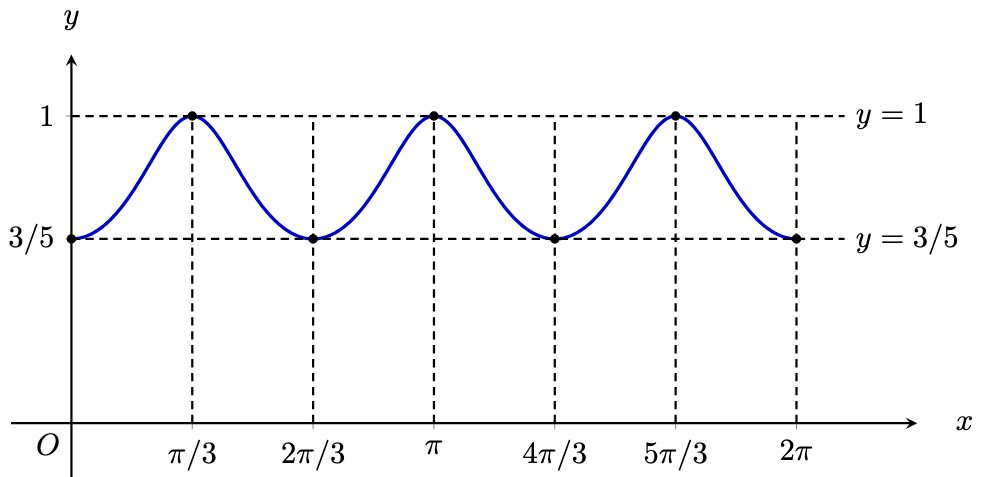
(b) (ii) We first note that the graph of $y = f(x)$ is defined on all of $\mathbb R$ , not just the domain $[0, 2\pi]$ . By considering reflections about vertical lines, we observe that the lines of symmetry of $y = f(x)$ are all of the form $x = k\pi/3$ , where $k$ is any integer (positive, zero, or negative).

(b) (iii) Since $\cos$ is $2\pi$ -periodic,

$\begin{aligned} \cos(3(x+\pi)) &= \cos(3x + 3\pi) \\ &= \cos(3x + \pi) \\ &= -{ \cos 3x }. \end{aligned}$

Hence,

$\displaystyle f(x+\pi) = \frac{A}{B + \cos(3(x+\pi))} = \frac{A}{B - \cos 3x} = \frac{3}{4 - \cos 3x}.$

(c) Using the product rule and the chain rule,

$\begin{aligned} \frac{\mathrm d^2 y}{\mathrm dx^2} &= \frac{\mathrm d}{\mathrm dx}(y^2 \sin 3x) \\ &= 2y \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \sin 3x + y^2 \cdot 3 \cos 3x \\ &= 2y \cdot y^2 \sin 3x \cdot \sin 3x + y^2 \cdot 3 \cos 3x \\ &= (3 \cos 3x) \cdot y^2 + (2 \sin^2 3x) \cdot y^3,\end{aligned}$

where $P(x) = 3 \cos 3x, Q(x) = 2 \sin^2 3x$ .

Question 4. Rate of Change

Solution. (a) Letting $T$ denote the time taken to fill the bowl,

$10\pi \cdot T = \frac 13 \pi \cdot 15^2 \cdot (45 - 15) \quad \Rightarrow \quad T = 225\, \text{s}.$

(b) Using the chain rule,

$\begin{aligned} \frac{\mathrm dV}{\mathrm dt} &= \frac{\mathrm dV}{\mathrm dh} \cdot \frac{\mathrm dh}{\mathrm dt} \\ &= {\textstyle \frac 13} \pi \cdot (2h \cdot (45-h) + h^2 \cdot (-1)) \cdot \frac{\mathrm dh}{\mathrm dt} \\ &= {\textstyle \frac 13} \pi \cdot h (90-3 h) \cdot \frac{\mathrm dh}{\mathrm dt}. \end{aligned}$

At $h = 12$ ,

$\begin{aligned} 10\pi &= {\textstyle \frac 13} \pi \cdot 12 (90-3 \cdot 12) \cdot \frac{\mathrm dh}{\mathrm dt}\Big|_{h = 12} \quad \Rightarrow \quad \frac{\mathrm dh}{\mathrm dt}\Big|_{h = 12} = \frac{5}{108 }\, \text{cm}\ \text{s}^{-1}.\end{aligned}$

(c) The total volume poured into the bowl after $T$ seconds is

$\displaystyle \int_0^T 10\pi t\, \mathrm dt = 10\pi \cdot \frac{T^2}{2} = 5\pi \cdot T^2.$

Since $T > 0$ , the required time taken is given by solving the equation:

$\displaystyle 5\pi \cdot T^2 = 972 \pi \quad \Rightarrow \quad T = \sqrt{194.4} \approx 13.9\, \text{s}.$

(d) At $V = 972\pi$ ,

$\frac 13 \pi h^2 (45 - h) = 972 \pi \quad \Rightarrow \quad h^3 -45h^2 + 2916= 0.$

Solving the cubic equation, $h = 43.455, 9, -7.4558$ . Since $h \in [0, 15]$ , we reject the first and last option and conclude $h = 9$ .

Therefore,

$\begin{aligned} 10\pi T &= {\textstyle \frac 13} \pi \cdot 9 (90-3 \cdot 9) \cdot \frac{\mathrm dh}{\mathrm dt}\Big|_{h = 9} \quad \Rightarrow \quad \frac{\mathrm dh}{\mathrm dt}\Big|_{h = 9} = \frac{10T}{189} \approx 0.738\, \text{cm}\ \text{s}^{-1}.\end{aligned}$

Section B: Probability and Statistics [60 marks]

Question 5. Probability

Solution. (a) The total number of counters is $3+5+7 = 15$ . The probability that the counters are of the same colours is given by

$\displaystyle \frac{3 \times 2 + 5 \times 4 + 7 \times 6}{15 \times 14} = \frac{34}{105}$

Hence, the required probability is its complement $1 - \frac{34}{105} = \frac{71}{105}$ .

(b) By pattern-recognition, the required equation to solve is:

$\displaystyle \frac{12!}{(13-n)!} \cdot \frac{(16-n)!}{15!} \cdot \frac{3}{16-n} = \frac{36}{455}.$

The left-hand side, using factorials, simplifies to

$\begin{aligned} \frac{12!}{(13-n)!} \cdot \frac{(16-n)!}{15!} \cdot \frac{3}{16-n} &= \frac{(15-n)(14-n)}{ 910 } . \end{aligned}$

Hence, we need to solve the quadratic equation

$\displaystyle \frac{(15-n)(14-n)}{ 910 } = \frac{36}{455}.$

Solving, we get $n = 6$ .

Question 6. Normal Distribution

Solution. (a) Using the symmetry of the normal distribution,

$\mathbb P(X < 7) = \mathbb P(X < \mu) - \mathbb P(7 \leq X < \mu) = 0.5 - 0.45 = 0.05.$

(b) Since $X \sim \mathcal N(\mu, 1.8^2)$ , we have

$\begin{aligned} 0.05 = \mathbb P(X < 7) &= \mathbb P\left(Z < \frac{7 - \mu}{1.8}\right). \end{aligned}$

Using $z$ -scores,

$\displaystyle \frac{7 - \mu}{1.8} = -1.6449 \quad \Rightarrow \quad \mu = 7 + 1.6449 \cdot 1.8 = 9.96082 \approx 9.96.$

(c) Using independence,

$\begin{aligned} 0.38 = \mathbb P((X > 7) \cap (Y > 7)) &= \mathbb P(X > 7) \cdot \mathbb P(Y > 7) \\ &= 0.95 \cdot \mathbb P(Y > 7). \end{aligned}$

By algebruh,

$\displaystyle \mathbb P(Y > 7) = \frac{0.38}{0.95} = 0.4\quad \Rightarrow \quad \mathbb P(Y \leq 7) = 0.6.$

Since $Y \sim \mathcal N(\lambda, 2.8^2)$ ,

$\displaystyle \mathbb P\left(Z \leq \frac{7 - \lambda}{2.8} \right) = \mathbb P(Y \leq 7) = 0.6.$

Using $z$ -scores,

$\displaystyle \frac{7 - \lambda}{2.8} = 0.25334 \quad \Rightarrow \quad \lambda = 7 - 2.8 \cdot 0.25334 = 6.2906 \approx 6.29.$

(d) Using complements,

$\begin{aligned} \mathbb P(Y \leq a) &= 1 - \mathbb P(Y > a) \\ &= 1 - 2 \cdot \mathbb P(Y > 7) \\ &= 1 - 2 \cdot 0.4 = 0.2. \end{aligned}$

Since $Y \sim \mathcal N(6.2906, 2.8^2)$ by (c), $a \approx 3.93$ .

Question 7. Permutations and Combinations

Solution. (a) The total number of arrangements, including repetitions, is

$\displaystyle \frac{8!}{2! \cdot 2!} = 10\, 080.$

(b) We first choose the start and end numbers, then place the third even number in the middle four spaces, and then permute the odd numbers:

$\displaystyle (3 \times 2) \times {4 \choose 1} \times \frac{5!}{2! \cdot 2!} = 720.$

(c) The total number of even-number groups (consisting of $2,4,8$ ) is $3! = 6$ . Hence, the required total is

$\displaystyle 3! \cdot \frac{6!}{2! \cdot 2!} = 1080.$

(d) We first count the number of arrangements where the even digits are all together and the odd digits are all together:

$\displaystyle 3! \cdot \frac{5!}{2! \cdot 2!} \cdot 2! = 360.$

The required probability is given by a conditional probability as follows:

$\displaystyle \frac{ 360 }{ 1080 } = \frac 13.$

Question 8. Correlation and Linear Regression

Solution. (a) Since $r = 0.39 \in (0.3, 0.7)$ , there is a weak positive linear correlation between the best performances of the athletes in the high jump and long jump events.

(b) (i) The diagram suggests that there is a positive, though non-linear, correlation between $x$ and $t$ , where $x$ increases at an increasing rate as $t$ increases.

(ii) For the model $t = ax+ b$ , we obtain a correlation coefficient of $r_1 \approx 0.958$ , and for the model $t = cx^2 + d$ we obtain a correlation coefficient of $r_2 \approx 0.990$ . Since $0 < r_1 < r_2 < 1$ (i.e. $|r_2|$ is closer to $1$ than $|r_1|$ ), the model $t = cx^2 + d$ is a better fit to the data. Furthermore, we obtain the regression equation

$\begin{aligned} t &= 1.24969x^2 + 0.87580 \\ t &= 1.25x^2 + 0.876.\quad (\text{3sf}) \end{aligned}$

(iii) At $x = 11$ ,

$t = 1.24969 \cdot 11^2 + 0.87580 \approx 152\, \text{minutes}.$

Since $r_2 \approx 0.990$ is close to $1$ , the correlation between $t$ and $x^2$ is strongly positive. Hence, an interpolation $x = 11 \in (2.1, 11)$ yields a reliable estimate.

Question 9. Binomial Distribution

Solution. (a) The two assumptions are as follows:
- The probability that a randomly chosen refrigerator is faulty is constant.
- The faultiness of any refrigerator is independent of other refrigerators.
(b) Since $X \sim \mathrm{B}(90, 0.02)$ , the required probability is

$\mathbb P(X > 1) = 1 - \mathbb P(X \leq 1) = 1 - 0.46043 = 0.53956 \approx 0.540.$

(c) Let $V \sim \mathrm{B}(5, 0.53956)$ denote the number of days in a $5$ -day working week, on which Alan finds more than one faulty refrigerator. The required probability is

$\mathbb P(V < 2) = \mathbb P(V \leq 1) = 0.14195 \approx 0.142.$

(d) Since $90 \times 5 = 450$ , let $W \sim \mathrm B(450, 0.02)$ denote the number of faulty refrigerators that Alan finds in total, in a $5$ -day work week. Then the required probability is

$\mathbb P(W < 10 ) = \mathbb P(W \leq 9) = 0.58741 \approx 0.587.$

(e) Since $X \sim \mathrm{B}(90, 0.02)$ and $X \sim \mathrm{B}(60, 0.03)$ , the required probability is given by three cases:

$\begin{aligned} \mathbb P(X + Y = 2) &= \mathbb P(X = 2) \cdot \mathbb P(Y = 0) + \mathbb P(X = 1) \cdot \mathbb P(Y = 1) + \mathbb P(X = 0) \cdot \mathbb P(Y = 2) \\ &= 0.27074 \cdot 0.16080 + 0.29812 \cdot 0.29840 + 0.16231 \cdot 0.27225 \\ &= 0.17668 \approx 0.177. \end{aligned}$

Question 10. Flour-Production

Solution. (a) In the question, $X$ denotes the mass, in kg, of packets produced by Machine $P$ , and $Y$ denotes the mass, in kg, of packets produced by Machine $Q$ . Since the machines are different and not related in general, the masses of packets of flour produced would also not affect one another. Therefore, $X,Y$ are independent.

(b) Let $X \sim \mathcal N( 2.2, 0.1^2 )$ denote the mass of a randomly chosen packet of flour produced by Machine $P$ . Let $Y \sim \mathcal N( 2.1, 0.05^2 )$ denote the mass of a randomly chosen packet of flour produced by Machine $Q$ . Then

$\begin{aligned} \mathbb E[X - Y] &= 2.2 - 2.1 = 0.1, \\ \mathrm{Var}(X - Y) &= 0.1^2 + 0.05^2 = 0.0125, \\ X- Y &\sim \mathcal N(0.1, 0.0125). \end{aligned}$

Hence, the required probability is

$\mathbb P(X > Y) = \mathbb P(X - Y > 0) = 0.81445 \approx 0.814.$

(c) Defining the random variable $W := X_1+ X_2 + X_3 + Y_1 + \cdots + Y_5$ ,

$\begin{aligned} \mathbb E[W] &= 3 \cdot 2.2 + 5 \cdot 2.1 = 17.1, \\ \mathrm{Var} (W) &= 3 \cdot 0.1^2 + 5 \cdot 0.05^2 = 0.0425. \end{aligned}$

Hence, $W \sim \mathcal N(17.1, 0.0425)$ , so that the required probabiltiy is

$\displaystyle \mathbb P(W > 17) = 0.68616 \approx 0.686.$

(d) Let $\mu$ denote the mean mass of a packet of flour, in kg, produced by the adjusted Machine $P$ . Then the null hypothesis $\mathrm H_0$ and the alternative hypothesis $\mathrm H_1$ are given as follows:

$\mathrm H_0 : \mu = 2.2,\quad \mathrm H_1 : \mu \neq 2.2.$

(e) Let $\bar x$ and $s^2$ denote the unbiased estimates of the population mean and variance of the relevant masses. Then

$\displaystyle \bar x = 2 + \frac{4.5}{30} = 2.15$

and

$\displaystyle s^2 = \frac{1}{30-1} \left( 1.11 - \frac{4.5^2}{30} \right) = 0.015.$

(f) Suppose $\mathrm H_0$ holds. Since the sample size $n = 30 \geq 0$ is sufficiently large, by the central limit theorem,

$\displaystyle \bar X \sim \mathcal N \left( 2.2, \frac{0.015}{30} \right)\quad \text{approximately}.$

Since we are conducting a two-tailed test, the required $p$ -value is given by

$p = 2 \cdot \mathbb P(\bar X \leq 2.15)= 2 \cdot 0.012673 \approx 0.0253 < 0.05.$

Since $p < 0.05$ , there is sufficient evidence to reject $\mathrm H_0$ and conclude that the mean mass of packets produced by the adjusted Machine $P$ differs from $2.2$ kg.

(g) If fewer than $30$ packets has been used, then the central limit theorem would lead to a weaker approximate normal distribution for $\bar X$ , yielding a possibly larger $p$ -value.

(h) If the sample had not been chosen randomly, it is plausible that the packets of flour chosen have masses that are not independent with one another, so that $\bar X$ may not follow a normal distribution, even approximately.

—Joel Kindiak, 7 Nov 25, 1522H
November 7, 2025
H2 Math 2025 Suggested Answers (Paper 1)
Questions have not been uploaded due to copyright reasons. Do comment if you spot any errors.

Question 1. Sequences and Series

Solution. (a) Setting $r = 1, 2, 3$ ,

$\begin{aligned} u_2 &= 3 u_1 + 5 = 3a + 5, \\ u_3 &= 3u_2 + 5 = 3(3a+5) + 5 = 9a + 20 \\ u_4 &= 3u_3 + 5 = 3(9a + 20) + 5 = 27a + 65.\end{aligned}$

(b) Using summation notation,

$\begin{aligned}110 = \sum_{r=1}^4 u_r &= u_1 + u_2 + u_3 + u_4 \\ &= a + (3a+5) + (9a+20) + (27a+65) \\ &= 40a + 90.\end{aligned}$

Solving the equation yields $a = 1/2$ .

Question 2. Arithmetic and Geometric Progression

Solution. (a) Let $u_n = a + (n-1)d$ denote the $n$ -th term of the arithmetic sequence, $n \geq 1$ . By considering the sum of the first $20$ terms, we have first term $a$ and last term $a + 19d$ so that

$\displaystyle \frac{20}{2} (a + (a+19d)) = 65 \quad \Rightarrow \quad 2a + 19d = 6.5.$

For the next $8$ terms, we have first term $a + 20d$ and last term $a + 27d$ so that

$\displaystyle \frac 82 ((a+20d) + (a + 27d)) = -30 \quad \Rightarrow \quad 2a + 47d = -7.5.$

Solving the system of linear equations yields $a = 8$ and $d = -1/2$ .

(b) By considering the ratio of consecutive terms,

$\begin{aligned} \frac{u_{n+1}}{u_n} = \frac{e^{k(n+2)}}{e^{k(n+1)}} = e^{k(n+2) - k(n+1)} = e^k \neq 1, \end{aligned}$

which is constant. Therefore, the sequence having a common ratio $e^k$ is a geometric sequence.

Question 3. Complex Numbers

Solution. (a) We first compute the modulus and argument of $\sqrt 3 \pm i$ :

$|\sqrt 3 \pm i| = \sqrt{(\sqrt 3)^2 + (\pm 1)^2} = 2,\quad \arg(\sqrt 3 \pm i) = \pm \frac 16 \pi.$

Therefore,

$\begin{aligned} |z| &= \frac{|\sqrt 3 + i|}{|\sqrt 3 - i|} = \frac{2}{2} = 1,\\ \arg(z) &= \arg(\sqrt 3 + i) - \arg(\sqrt 3 - i) \\ &= \textstyle \frac 16 \pi - \left(-\frac 16 \pi\right) = \frac 13 \pi. \end{aligned}$

(b) The Argand diagram is drawn below.

The point $B$ represents the complex number $iz$ .

Question 4. Optimisation

Solution. (a) We first write the function as $y = (3x+10)(x+1)^{-1/2}$ . Using the product rule,

$\begin{aligned} \frac{\mathrm dy}{\mathrm dx} &= \textstyle 3 \cdot (x+1)^{-1/2} + (3x+10) \cdot \left(-\frac 12 \right) (x+1)^{-3/2} \\ &=\textstyle \frac 12(x+1)^{-3/2} \left( 2 \cdot 3 \cdot (x+1) + (3x+10) \cdot (-1) \right) \\ &=\textstyle \frac 12(x+1)^{-3/2} \left( 6x+6 - (3x+10) \right) \\ &=\textstyle \frac 12(x+1)^{-3/2} ( 3x - 4).\end{aligned}$

At the turning point, $\displaystyle \frac{\mathrm dy}{\mathrm dx} = 0$ so that

$\textstyle \frac 12(x+1)^{-3/2} ( 3x - 4) = 0 \quad \Rightarrow \quad x = \frac 43.$

(b) We use the product rule again to obtain

$\begin{aligned} \frac{\mathrm d^2y }{\mathrm dx^2} &= \textstyle \frac 12 \left( -\frac 32 \cdot (x+1)^{-5/2} ( 3x - 4) + (x+1)^{-3/2} \cdot 3 \right).\end{aligned}$

At the turning point, $x = 4/3$ yields

$\begin{aligned} \frac{\mathrm d^2 y }{\mathrm dx^2} \Big|_{x=4/3} &= \textstyle \frac 12 \left( 0 + (\frac 43+1)^{-3/2} \cdot 3 \right) = \frac 32 \cdot \left( \frac 73 \right)^{-3/2} \approx 0.421 > 0.\end{aligned}$

Hence, the turning point is a local minimum.

Question 5. Inequalities

Solution. (a) Make the substitution $u = e^x > 0$ , so that we solve the inequality

$\begin{aligned} u &\geq 2u^{-1} + 1 \\ u^2 & \geq 2 + u \\ u^2 - u - 2 &\geq 0 \\ (u-2)(u+1) &\geq 0. \end{aligned}$

Therefore, $u \leq -1$ (which we reject since $u > 0$ ) or

$u-2 \geq 0 \quad \Leftrightarrow \quad u \geq 2\quad \Leftrightarrow \quad e^x \geq 2 \quad \Leftrightarrow \quad x \geq \ln 2.$

(b) By part (a),

$x \geq \ln 2 \quad \Leftrightarrow \quad e^x \geq 2e^{-x} + 1 \quad \Leftrightarrow \quad e^x - 2e^{-x} - 1 \geq 0.$

We first calculate the indefinite integral for convenience:

$\displaystyle f(x) := \int (e^x - 2e^{-x} - 1)\, \mathrm dx = e^x + 2e^{-x} - x + C.$

Since $\ln 2 \approx 0.693 \in (0, 1)$ , we split the integral into two parts:

$\begin{aligned} \int_0^1 |e^x - 2e^{-x} - 1|\, \mathrm dx &= -\int_0^{\ln 2} (e^x - 2e^{-x} - 1)\, \mathrm dx + \int_{\ln 2}^{1} (e^x - 2e^{-x} - 1)\, \mathrm dx \\ &= -(f(\ln 2) - f(0)) + (f(1) - f(\ln 2)) \\ &= f(1) - 2 f(\ln 2) + f(0) \\ &= (e^1 + 2e^{-1} - 1) - 2 (e^{\ln 2} + 2e^{-\ln 2} - \ln 2) + (1 + 2 - 0) \\ &= (e + 2/e - 1) - (6 - 2\ln 2) + 3 \\ &= e + 2/e + 2\ln 2 - 4.\end{aligned}$

Question 6. Radioactive Decay

Solution. (a) Using the method of separable variables,

$\begin{aligned} \int \frac{1}{M}\, \mathrm dM &= \int -k\, \mathrm dt \\ \ln |M| &= -kt + C \\ M &= \pm e^C \cdot e^{-kt} \\ &= Ae^{-kt}.\end{aligned}$

By the question, setting $t = 0$ yields

$M_0 = Ae^{-k\cdot 0} = A \quad \Rightarrow \quad M = M_0 \cdot e^{-kt}.$

Furthermore, $M = M_0/2$ when $t = 5730$ :

$\begin{aligned} \frac{M_0}{2} &= M_0 \cdot e^{-k \cdot 5730} \\ \frac 12 &= e^{-5730 k} \\ k &= \frac{\ln 2}{5730} \approx 1.21 \times 10^{-4}. \end{aligned}$

(b) Letting $T$ denote the time passed (in years), we solve the equation

$\begin{aligned} 0.2M_0 &= M_0 \cdot e^{-kT} \\ T &= \frac{ \ln 0.2 }{-k} \\ &= \ln 0.2 \cdot \left( - \frac{5730}{\ln 2} \right) \\ &= 13\, 304 \\ &\approx 13\, 300. \end{aligned}$

Therefore the plant died $13\, 300$ years ago, correct to 3 significant figures.

Question 7. Volume of Revolution

Solution. (a) Using linearity and the product rule,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (x \ln x - x ) &= \frac{\mathrm d}{\mathrm dx}(x \ln x) - \frac{\mathrm d}{\mathrm dx}(x) \\ &= 1 \cdot \ln x + x \cdot \frac 1x - 1 \\ &= \ln x. \end{aligned}$

(b) Using (a),

$\displaystyle \int \ln x\, \mathrm dx = x \ln x - x + C.$

At the $x$ -axis, $\ln x = 0 \Rightarrow x = 1$ . Therefore, the required volume of revolution $V_1$ is

$\begin{aligned}V_1 &= \pi \int_1^e (\ln x)^2\, \mathrm dx \\ &= \pi \left( \left[\underbrace{ (x \ln x - x) }_{\mathrm I} \cdot \underbrace{ \ln x }_{\mathrm S}\right]_1^e - \int_1^e \underbrace{ (x \ln x - x) }_{\mathrm I} \cdot \underbrace{ \frac 1x }_{\mathrm D}\, \mathrm dx \right) \\ &= \pi \left( (0 - 0) - \int_1^e (\ln x - 1)\, \mathrm dx \right) \\ &= \pi \int_1^e (1 - \ln x )\, \mathrm dx \\ &= \pi [ x - (x \ln x - x)]_1^e \\ &= \pi [ 2x - x \ln x ]_1^e \\ &= \pi \cdot ( (2e - e) - (2 - 0) ) \\ &= \pi (e-2)\, \text{units}^3.\end{aligned}$

(c) The curve $y = \ln(x)$ is equivalently given by $x = e^y$ . Therefore, the required volume of revolution $V_2$ is

$\begin{aligned} V_2 &= \pi e^2 \cdot 1 - \pi \int_0^1 (e^y)^2\, \mathrm dy \approx 13. 18\, \text{units}^3\, (\text{2dp}). \end{aligned}$

Remark 1. The exact volume for $V_2$ is $V_2 = \frac 12\pi (e^2 + 1)\, \text{units}^3$ , left as a simple exercise in integration.

Question 8. Vectors

Solution. (a) We first write $\pi_1$ in scalar product form:

$\pi_1 : \mathbf r \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} = 2.$

The line $\ell$ perpendicular to $\pi_1$ passing through $P$ has vector equation

$\ell : \mathbf r = \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix},\quad \lambda \in \mathbb R.$

The foot of perpendicular $F$ is given by the intersection of $\ell$ and $\pi_1$ :

$\begin{aligned} \left( \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \right) \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} &= 2 \\ \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} + \lambda \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} &= 2 \\ -5 +14 \lambda &= 2 \\ \lambda &= \textstyle \frac 12.\end{aligned}$

Therefore,

$\overrightarrow{OF} = \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} + \frac 12 \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} = \begin{bmatrix} -2 \\ 3/2 \\ 3/2 \end{bmatrix}\quad \Rightarrow \quad F(-2, 3/2, 3/2).$

(b) Let $Q$ denote the reflection of $P$ in $\pi_1$ . By the midpoint theorem,

$\overrightarrow{OF} = \frac 12 (\overrightarrow{OP} + \overrightarrow{OQ}).$

Therefore,

$\begin{aligned} \overrightarrow{OQ} &= 2 \overrightarrow{OF} - \overrightarrow{OP} = 2 \begin{bmatrix} -2 \\ 3/2 \\ 3/2 \end{bmatrix} - \begin{bmatrix} -3 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \\ 3 \end{bmatrix}. \end{aligned}$

(c) The normal vector of $\pi_2$ is given by the cross product:

$\begin{bmatrix} 2 \\ -1 \\ 5 \end{bmatrix} \times \begin{bmatrix} 2 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix}.$

The acute angle $\alpha$ between $\pi_1, \pi_2$ is given by the dot product between their normal vectors:

$\begin{aligned} \left|\begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \cdot \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix} \right| &= \left\| \begin{bmatrix} 2 \\ 1 \\ 3 \end{bmatrix} \right\| \left\| \begin{bmatrix} -13 \\ 4 \\ 6 \end{bmatrix} \right\| \cos \alpha \\ 4 &= \sqrt{14} \sqrt{221} \cos \alpha \\ \cos \alpha &= \frac{4}{\sqrt{14}\sqrt{221} } \\ \alpha &\approx 85.9^\circ. \end{aligned}$

Question 9. Power Series

Solution. (a) Using implicit differentiation,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (\sin y) &= \frac{\mathrm d}{\mathrm dx}(px) \\ \cos y \cdot \frac{\mathrm dy}{\mathrm dx} &= p \\ \frac{\mathrm dy}{\mathrm dx} &= \frac{p}{\cos y} \\ &= p \sec y.\end{aligned}$

(b) Using implicit differentiation two more times,

$\begin{aligned} \frac{\mathrm d^2 y }{\mathrm dx^2} &= p \cdot \sec y \tan y \cdot \frac{\mathrm dy}{\mathrm dx} \\ &= \tan y \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^2 \\ \frac{\mathrm d^3 y}{\mathrm dx^3} &= \sec^2 y \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^2 + \tan y \cdot 2 \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm d^2 y}{\mathrm dx^2} \\ &= \sec^2 y \cdot \left(\frac{\mathrm dy}{\mathrm dx} \right)^3 + 2\tan y \cdot \frac{\mathrm dy}{\mathrm dx} \cdot \frac{\mathrm d^2 y}{\mathrm dx^2}. \end{aligned}$

Setting $x = 0$ ,

$\begin{aligned} y &= \sin^{-1} 0 = 0, \\ \frac{\mathrm dy}{\mathrm dx} &=p \sec 0 = p, \\ \frac{\mathrm d^2 y }{\mathrm dx^2} &= \tan 0 \cdot p^2 = 0, \\ \frac{\mathrm d^3 y }{\mathrm dx^3} &= \sec^2 0 \cdot p^3 + 2\tan 0 \cdot p \cdot 0 = p^3. \end{aligned}$

Therefore, the Maclaurin series for $y$ up to and including the term in $x^3$ is given by

$\displaystyle y \approx 0 + px + \frac{0}{2!} \cdot x^2 + \frac{p^3}{3!} \cdot x^3 = px + \frac{p^3}{6} \cdot x^3.$

(c) Differentiating term-by-term,

$\begin{aligned} \frac{\mathrm d}{\mathrm dx} (\sin^{-1} px) &\approx \frac{\mathrm d}{\mathrm dx} \left( px + \frac{p^3}{6} \cdot x^3 \right) \\ \frac 1{\sqrt{1 - (px)^2}} \cdot p &\approx p + \frac{p^3}{6} \cdot 3x^2 \\ \frac 1{\sqrt{1 - p^2 x^2}} &\approx 1 + \frac{p^2}{2} \cdot x^2. \end{aligned}$

Setting $p = 3$ (so that $p^2 = 9$ ) yields the series expansion

$\displaystyle \frac 1{\sqrt{1 - 9x^2}} \approx 1 + \frac 92 \cdot x^2.$

Question 10. Functions

Solution. (a) The graph has asymptotes $y = -a$ , $x = -b$ and axial intercepts $(4/a, 0)$ , $(0, 4/b)$ .

(b) We first use algebra (or long division) to obtain

$\displaystyle f(x) =\frac{4-ax}{x+b} = -a + \frac{4+ ab}{x+b}.$

Therefore, we make the following transformations:
- Translate by $a$ units in the positive $y$ -direction.
- Scale by a factor of $1/(4+ab)$ parallel to the $y$ -axis.
- Translate by $b$ units in the positive $x$ -direction.
(c) Denote $y = f^{-1}(x) \Leftrightarrow x = f(y)$ so that

$\begin{aligned}x &= -a + \frac{4+ab}{y+b} \\ x+a &= \frac{4+ab}{y+b} \\ y+b &= \frac{4+ab}{x+a} \\ y &= -b + \frac{4 + ab}{x+a} \\ f^{-1}(x) &= -b + \frac{4 + ab}{x+a}.\end{aligned}$

Furthermore, $\text{R}_{f^{-1}} = \text{D}_{f} = (-\infty, -b) \cup (-b, \infty) \equiv \mathbb R \backslash \{-b\}$ .

(d) Given $b = a$ ,

$\displaystyle f^{-1}(x) = -a + \frac{4+a^2}{x+a} = f(x) \quad \Rightarrow \quad f^2(x) = x.$

Since $2025 = 2 \cdot 1012 + 1$ ,

$\displaystyle f^{2025}(2) = f(2) = -a + \frac{4+a^2}{2+a}.$

Question 11. Roller Coaster

Solution. (a) Differentiating with respect to $\theta$ ,

$\begin{aligned} \frac{\mathrm dx}{\mathrm d\theta} &= 28 \cdot (\cos \theta + \theta \cdot (-\sin \theta ) ) \\ &= 28 (\cos \theta - \theta \sin \theta ),\\ \frac{\mathrm dy}{\mathrm d\theta} &= 20 \cdot ( - (1 \cdot \sin \theta + \theta \cdot \cos \theta ) ) \\ &= -20(\sin \theta + \theta \cos \theta ). \end{aligned}$

By an application of the chain rule,

$\displaystyle \frac{\mathrm dy}{\mathrm dx} = \frac{-20(\sin \theta + \theta \cos \theta )}{ 28 (\cos \theta - \theta \sin \theta ) } = -\frac{5(\sin \theta + \theta \cos \theta )}{ 7 (\cos \theta - \theta \sin \theta ) }.$

(b) (i) At $C$ and $D$ , the denominator of $\displaystyle \frac{\mathrm dy}{\mathrm dx}$ is $0$ :

$\displaystyle 7 (\cos \theta - \theta \sin \theta ) = 0 \quad \Rightarrow \quad \cos \theta = \theta \sin \theta .$

Therefore, $\theta = \pm 0.8603 \approx \pm 0.86\ (\text{2sf})$ .

(b) (ii) The $x$ -coordinates of $C,D$ are $12.289$ and $43.710$ respectively. Hence,

$CD = 43.710 - 12.289 = 31.421 \approx 31.4\, \text{units}.$

(c) (i) We solve the equation

$28(\theta \cos \theta + 1) = 28 \quad \Rightarrow \quad \theta \cos \theta = 0.$

Therefore, $\theta = 0$ or $\cos \theta = 0\Rightarrow \theta = \pm \pi/2$ . By substituting into expression for $y$ ,

$\displaystyle y = 10(4 - \pi), 40, 10(4-\pi)$

respectively. Hence, $\theta = 0$ at $A$ .

(c) (ii) Furthermore, $\theta = \pm \pi/2$ at $B$ .

(c) (iii) Consequently, $AB = 40 - (10(4-\pi)) = 10\pi \approx 31.4\, \text{units}$ .

(d) The $y$ -coordinates of $E$ and $D$ are equal:

$\displaystyle y = 20(2 - 0.8603 \sin 0.8603 ) = 26.957.$

Therefore, $AE = 40 - 26.957 = 13.042$ . Since

$\frac 12 CD = \frac 12 \cdot 31.421 = 15.7105,$

the margin of error $\epsilon$ is given by

$\epsilon := 10\% \cdot \frac 12 CD = 0.1 \cdot 15.7105 = 1.57105.$

In particular, we require

$AE \in (\frac 12 CD - \epsilon, \frac 12 CD + \epsilon) = (14.13945, 17.28155),$

which does not hold. In particular, this section of the track does not satisfy the safety condition.

Question 12. Complex Numbers

(a) Since the coefficients of the given polynomial equation are all real, by the conjugate root theorem, a second root is given by $1 - 2i$ .

(b) Given $z = 1+2i$ , we evaluate $z^2$ and $z^3$ :

$\begin{aligned} z^2 &= 1^2 + 2 \cdot 1 \cdot 2i + (2i)^2 = -3 + 4i, \\ z^3 &= 1^3 + 3 \cdot 1^2 \cdot 2i + 3 \cdot 1 \cdot (2i)^2 + (2i)^3 \\ &= 1 + 6i - 12 -8i \\ &= -11 - 2i. \end{aligned}$

Therefore, substituting $z = 1+2i$ ,

$\begin{aligned}(1+2i)^3 + p(1+2i)^2 + q(1+2i) - 10 &= 0 \\ (-11 - 2i) + p(-3 + 4i) + q(1+2i) - 10 &= 0 \\ (- 3p + q - 21) + (-2 + 4p + 2q)i = 0. \end{aligned}$

Comparing real and imaginary parts,

$\begin{aligned}3p - q &= -21, \\ 4p+2q &= 2.\end{aligned}$

Solving the system of linear equations, $p = -4, q = 9$ .

The given polynomial has a quadratic factor given by

$\begin{aligned} (z - (1 + 2i))(z-(1-2i)) &= z^2 - ((1+2i)z + (1-2i)z) + (1+2i)(1-2i) \\ &= z^2 - 2z + 5. \end{aligned}$

Therefore, we factorise

$z^3 -4z + 9z - 10 = (z^2 - 2z + 5)(z - 2).$

Therefore, the third root is $z = 2$ .

(c) Dividing by $w^3$ on both sides,

$\displaystyle \left( \frac 1w \right)^3 + p \left( \frac 1w \right)^2 + q \cdot \frac 1w - 10 = 0.$

Therefore, $1/w = z \Leftrightarrow w = 1/z$ . For $z = 1+2i$ ,

$\displaystyle w = \frac 1{1+2i} \cdot \frac{1-2i}{1-2i} = \textstyle \frac 15 (1-2i) = \frac 15 - \frac 25 i.$

For $z = 1-2i = (1+2i)^*$ ,

$\displaystyle w = \frac 1{1-2i} = \left(\frac 1{1+2i} \right)^* = \textstyle \left( \frac 15 - \frac 25 i \right)^* = \frac 15 + \frac 25 i.$

Finally, for $z = 2$ , $w = 1/2$ . Therefore, the three roots are $\frac 15 \pm \frac 25 i$ and $1/2$ .

—Joel Kindiak, 4 Nov 25, 1525H
November 4, 2025