Recall that  and
and  for any
for any  .
.
Definition 1. For any function  , define
, define  by
by  .
.
Problem 1. Given functions  , define
, define  and
and  . Prove that
. Prove that  and
and  .
.
(Click for Solution)
Solution. By definition,

and

Definition 2. A function  is odd (resp. even) if there exists an odd (resp. even) integer
is odd (resp. even) if there exists an odd (resp. even) integer  such that
such that  .
.
Example 1. For any integer  , the function
, the function 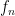 defined by
defined by  is an odd (resp. even) function if and only if
is an odd (resp. even) function if and only if  is an odd (resp. even) number. Furthermore,
is an odd (resp. even) number. Furthermore,  is an odd function while
is an odd function while 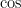 is an even function.
is an even function.
Problem 2. For any function  and real number
and real number  , define the function
, define the function  by
by  . In particular,
. In particular,  . Prove that
. Prove that  is odd (resp. even) if
is odd (resp. even) if  is odd (resp. even).
is odd (resp. even).
(Click for Solution)
Solution. We observe that if  is odd or even, then
is odd or even, then  , so that
, so that

hence  .
.
Problem 3. Prove the following properties:
- if
 are odd, then
are odd, then  is odd and
is odd and 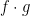 is even,
is even,
- if
 are even, then
are even, then  is even and
is even and 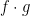 is even,
is even,
- if
 is odd and
is odd and 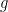 is odd (resp. even), then
is odd (resp. even), then  is odd (resp. even) whenever it exists.
is odd (resp. even) whenever it exists.
- if
 is even, then
is even, then  is even.
is even.
(Click for Solution)
Solution. Suppose  and
and  , and assume
, and assume  for simplicity. Denote
for simplicity. Denote  and
and  as per Problem 1. Then
as per Problem 1. Then

If  and
and  are both odd or both even, then
are both odd or both even, then  is even, so that
is even, so that

Hence, 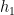 is odd (resp. even) if and only if
is odd (resp. even) if and only if  is odd (resp. even). Similarly,
is odd (resp. even). Similarly,

If  and
and  are both odd or both even, then
are both odd or both even, then  is always even, so that
is always even, so that  unconditionally, i.e.
unconditionally, i.e.  is even. For the composite function, define
is even. For the composite function, define  . Then
. Then

Applying the odd or even condition on  ,
,

If  is odd, then
is odd, then  is even, so that
is even, so that

Thus, 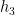 is odd (resp. even) if and only if
is odd (resp. even) if and only if 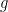 is odd (resp. even). If
is odd (resp. even). If  is even, then
is even, then

so that 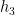 is even.
is even.
Problem 4. For any function  , prove that there exist a unique odd function
, prove that there exist a unique odd function  and a unique even function
and a unique even function 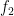 such that
such that  .
.
(Click for Solution)
Solution. For existence, define the functions  by
by

It is obvious that  . Since
. Since  ,
,

so that  is odd and
is odd and 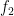 is even. For uniqueness, suppose
is even. For uniqueness, suppose  , where
, where  is odd and
is odd and  is even. Then
is even. Then  , so that
, so that 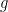 is both odd and even. Hence,
is both odd and even. Hence,

Problem 5. Fix 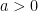 , any odd continuous function
, any odd continuous function  , and any even continuous function
, and any even continuous function 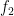 . Prove that
. Prove that

In particular, for any continuous function  ,
,

(Click for Solution)
Solution. Using a substitution,

Therefore,

Similarly, we can prove that

so that

Problem 6. For any continuous function  and
and  , define
, define

Prove that  (resp.
(resp.  ) if
) if  is odd (resp. even).
is odd (resp. even).
(Click for Solution)
Solution. By Example 1 and Problem 2,  is even and
is even and  is odd.
is odd.
Thus, if  is odd, then
is odd, then  is odd by Problem 3, so that
is odd by Problem 3, so that  by Problem 5.
by Problem 5.
Similarly, if  is even, then
is even, then  is odd by Problem 3, so that
is odd by Problem 3, so that  by Problem 5.
by Problem 5.
—Joel Kindiak, 5 Aug 25, 2044H
to mean that
as
. In particular, if
is continuous at
and
for
, then
.
is a root of
,
is a factor of
:
. Hence,
, so that
leads to
. Then
.
.
on both the numerator and the denominator,