KindiakMath

Category: Exercises

A Painful Fourier Computation

Problem 1. Evaluate the Fourier series of the function $f$ defined by $f(t) := |t-1|$ on $[-2, 2)$ with periodic extension $f(t) = f(t+4)$ .

(Click for Solution)

Solution. By definition of the absolute value function,

$f(t) = \begin{cases} 1-t,\quad t \in [-2, 1], \\ t-1, \quad t \in [ 1, 2). \end{cases}$

We first use this decomposition to compute the odd and even parts of $f$ : for $t > 0$ ,

$\displaystyle \begin{aligned} f_{\mathrm{even}}(t) &= \frac{f(t) + f(-t)}{2} = \begin{cases} 1, & t \in [0, 1], \\ t, & t \in [1, 2),\end{cases} \\ f_{\mathrm{odd}}(t) &= \frac{f(t) - f(-t)}{2} = \begin{cases} -t, & t \in [0, 1], \\ -1, & t \in [1, 2).\end{cases} \end{aligned}$

Now integrating by parts,

$\begin{aligned} \int u \cos u\, \mathrm du &= u \sin u + \cos u + C, \\ \int u \sin u\, \mathrm du &= -u \cos u +\sin u + C. \end{aligned}$

Evaluating the Fourier coefficient $a_0$ ,

$\begin{aligned} a_0 &= \frac 12 \int_{-2}^2 f(t)\, \mathrm dt = \frac 12 \int_{-2}^2 f_{\mathrm{even}}(t)\, \mathrm dt = \int_0^2 f_{\mathrm{even}}(t)\, \mathrm dt = \frac 52. \end{aligned}$

Similarly, evaluating the Fourier coefficients $a_n, b_n$ using the substitution $u = n\pi t/ 2$ where needed,

$\begin{aligned} a_n &= \frac 12 \int_{-2}^2 f_{\text{even}}(t) \cos \left( \frac{n\pi t}{2} \right)\, \mathrm dt = \frac 2{n\pi} \int_0^{n \pi} f_{\text{even}}\left( \frac 2{n\pi} u \right) \cos u \, \mathrm du, \\ b_n &= \frac 12 \int_{-2}^2 f_{\text{odd}}(t) \sin \left( \frac{n\pi t}{2} \right)\, \mathrm dt = \frac 2{n\pi} \int_0^{n \pi} f_{\text{odd}}\left( \frac 2{n\pi} u \right) \sin u \, \mathrm du \end{aligned}$

All that remains is evaluating these integrals piece-wise:

$\begin{aligned} \int_0^2 f_{\text{even}}\left( \frac 2{n\pi} u \right) \cos u \, \mathrm du &= \int_0^{n\pi/2} \cos u \, \mathrm du + \int_{n\pi/2}^{n\pi} \frac 2{n\pi} u \cos u \, \mathrm du \\ &= \left[\sin u \right]_0^{n\pi/2} + \frac 2{n\pi} \left[u \sin u - \cos u\right]_{n\pi/2}^{n\pi} \\ &= \sin \frac{n \pi} 2 + \frac 2{n\pi} \left( \cos(n \pi) - \left( \frac{n \pi}{2} \sin \frac{n \pi}{2} + \cos \frac{n \pi}{2} \right)\right) \\ &= \frac 2{n\pi} \left((-1)^n - \left( \cos \frac{n \pi}{2} \right)\right), \\ \int_0^2 f_{\text{odd}}\left( \frac 2{n\pi} u \right) \sin u \, \mathrm du &= -\frac 2{n\pi} \int_0^{n\pi/2} u \sin u \, \mathrm du - \int_{n\pi/2}^{n\pi} \sin u \, \mathrm du \\ &= -\frac 2{n\pi} \left[ -u \cos u + \sin u \right]_0^{n\pi/2} - \left[-\cos u\right]_{n\pi/2}^{n\pi} \\ &= \frac 2{n\pi} \left[ u \cos u - \sin u \right]_0^{n\pi/2} + \left[\cos u\right]_{n\pi/2}^{n\pi} \\ &= \frac 2{n\pi} \left( \left( \frac{n \pi}{2} \cos \frac{n \pi}{2} - \sin \frac{n \pi}{2} \right) - \sin(n \pi) \right) \\ & \phantom{==} + \left( \cos n\pi - \cos \frac{n \pi} 2\right) \\ &= -\frac 2{n\pi} \sin \frac{n \pi}{2} + \cos n\pi = (-1)^n -\frac 2{n\pi} \sin \frac{n \pi}{2} . \end{aligned}$

Therefore, we obtain the awfully long Fourier series

$\begin{aligned} f(t) &= \frac 54 + \frac 2{n \pi} \sum_{n=1}^\infty \left[ \frac 2{n\pi} \left((-1)^n - \left( \cos \frac{n \pi}{2} \right)\right) \cos \frac{n \pi t}{2} \right. \\ &\phantom{=========} \left.+ \left( (-1)^n -\frac 2{n\pi} \sin \frac{n \pi}{2} \right) \sin \frac{n \pi t}{2} \right]. \end{aligned}$

This question was posed in one of my polytechnic’s final examinations.

—Joel Kindiak, 30 Aug 25, 2240H

November 7, 2025
The Triple Combo

Let $\mathbf A \in \mathcal M_{2 \times 2}(\mathbb K)$ be a symmetric matrix with associated bilinear form $[\mathbf u, \mathbf v ]_{\mathbf A} = \mathbf u^{\mathrm T} \mathbf A \mathbf v$ and quadrance $Q_{\mathbf A}(\mathbf v) = [\mathbf v, \mathbf v]_{\mathbf A}$ . For $\mathbf u, \mathbf v$ with nonzero quadrances, define the spread by

$\displaystyle s_{\mathbf A}(\mathbf u, \mathbf v) := 1 - \frac{[\mathbf u, \mathbf v]_{\mathbf A}^2}{Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v)}.$

Problem 1. Define the Gram matrix by

$\mathbf G_{\mathbf A}(\mathbf u, \mathbf v) = \begin{bmatrix} [\mathbf u, \mathbf u ]_{\mathbf A} & [\mathbf u, \mathbf v ]_{\mathbf A} \\ [\mathbf v, \mathbf u ]_{\mathbf A} & [\mathbf v, \mathbf v ]_{\mathbf A} \end{bmatrix}.$

Using the Gram matrix, or otherwise, prove that

$Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v) = [\mathbf u, \mathbf v]^2 + \det(\mathbf A) \det(\mathbf u, \mathbf v)^2.$

Deduce that

$\displaystyle s_{\mathbf A}(\mathbf u, \mathbf v) = \frac{\det(\mathbf A) \det(\mathbf u, \mathbf v)^2}{Q_{\mathbf A}(\mathbf u) Q_{\mathbf A}(\mathbf v)}.$

(Click for Solution)

Solution. We first observe that the Gram matrix can be written as a product of matrices:

$\displaystyle \begin{aligned} \mathbf G_{\mathbf A}(\mathbf u, \mathbf v) &= \begin{bmatrix} [\mathbf u, \mathbf u ]_{\mathbf A} & [\mathbf u, \mathbf v ]_{\mathbf A} \\ [\mathbf v, \mathbf u ]_{\mathbf A} & [\mathbf v, \mathbf v ]_{\mathbf A} \end{bmatrix} \\ &= \begin{bmatrix} \mathbf u^{\mathrm T} \mathbf A \mathbf u & \mathbf u^{\mathrm T} \mathbf A \mathbf v \\ \mathbf v^{\mathrm T} \mathbf A \mathbf u & \mathbf v^{\mathrm T} \mathbf A \mathbf v \end{bmatrix} \\ &= \begin{bmatrix} \mathbf u^{\mathrm T} \\ \mathbf v^{\mathrm T} \end{bmatrix} \mathbf A \begin{bmatrix}\mathbf u & \mathbf v \end{bmatrix} \\ &= \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix}^{\mathrm T} \mathbf A \begin{bmatrix}\mathbf u & \mathbf v \end{bmatrix} \end{aligned}$

Taking determinants,

$\begin{aligned} |\mathbf G_{\mathbf A}(\mathbf u,\mathbf v)| &= \left| \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix}^{\mathrm T} \right| \det(\mathbf A) \left| \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix} \right| \\ &=\left| \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix}^{\mathrm T} \right| \det(\mathbf A) \left| \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix}^{\mathrm T} \right| \\ &=\det(\mathbf A) \left| \begin{bmatrix} \mathbf u & \mathbf v \end{bmatrix}^{\mathrm T} \right|^2 \\ &=\det(\mathbf A) \det(\mathbf u, \mathbf v)^2 \end{aligned}$

On the other hand, by the symmetry of $[\cdot, \cdot]_{\mathbf A}$ , directly computing $|\mathbf G_{\mathbf A}(\mathbf u,\mathbf v)|$ yields

$\begin{aligned}|\mathbf G_{\mathbf A}(\mathbf u,\mathbf v)| &= \left| \begin{bmatrix} [\mathbf u, \mathbf u ]_{\mathbf A} & [\mathbf u, \mathbf v ]_{\mathbf A} \\ [\mathbf v, \mathbf u ]_{\mathbf A} & [\mathbf v, \mathbf v ]_{\mathbf A} \end{bmatrix} \right| \\ &= [\mathbf u, \mathbf u ]_{\mathbf A} [\mathbf v, \mathbf v ]_{\mathbf A} - [\mathbf u, \mathbf v ]_{\mathbf A} [\mathbf v, \mathbf u ]_{\mathbf A} \\ &= Q_{\mathbf A}(\mathbf u) Q_{\mathbf A}(\mathbf v) - [\mathbf u, \mathbf v]_{\mathbf A}^2. \end{aligned}$

Therefore,

$Q_{\mathbf A}(\mathbf u) Q_{\mathbf A}(\mathbf v) - [\mathbf u, \mathbf v]_{\mathbf A}^2 = \det(\mathbf A) \det(\mathbf u, \mathbf v)^2,$

yielding the desired result. For the spread, we use its definition to conclude

$\displaystyle \begin{aligned} s_{\mathbf A}(\mathbf u, \mathbf v) &= 1 - \frac{[\mathbf u, \mathbf v]_{\mathbf A}^2}{Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v)} \\ &= \frac{ Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v) - [\mathbf u, \mathbf v]_{\mathbf A}^2}{Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v)} \\ &= \frac{ \det(\mathbf A) \det(\mathbf u, \mathbf v)^2}{Q_{\mathbf A}(\mathbf u)Q_{\mathbf A}(\mathbf v)}. \end{aligned}$

Problem 2. Define the symmetric matrices $\mathbf I, \mathbf J, \mathbf K \in \mathcal M_{2 \times 2}(\mathbb K)$ by

$\mathbf I := \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix},\quad \mathbf J := \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix},\quad \mathbf K := \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}.$

Prove that for $\mathbf u, \mathbf v$ with nonzero spreads (with respect to all three matrices),

$\displaystyle \frac{1}{s_{\mathbf I}(\mathbf u, \mathbf v)} + \frac{1}{s_{\mathbf J}(\mathbf u, \mathbf v)} + \frac{1}{s_{\mathbf K}(\mathbf u, \mathbf v)} = 2.$

(Click for Solution)

Solution. We first observe that $\det(\mathbf I) = 1$ and $\det(\mathbf J) = \det(\mathbf K) = -1$ . Using Problem 1, it suffices to prove that

$Q_{\mathbf I}(\mathbf u)Q_{\mathbf I}(\mathbf v) - Q_{\mathbf J}(\mathbf u)Q_{\mathbf J}(\mathbf v) - Q_{\mathbf K}(\mathbf u)Q_{\mathbf K}(\mathbf v) = 2 \det(\mathbf u,\mathbf v)^2.$

Writing $\mathbf u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}$ and $\mathbf v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}$ , a direct computation yields

$Q_{\mathbf I}(\mathbf u) = u_1^2 +u_2^2, \quad Q_{\mathbf J}(\mathbf u) = u_1^2 - u_2^2, \quad Q_{\mathbf K}(\mathbf u) = 2u_1u_2.$

On the other hand, $\det(\mathbf u,\mathbf v)^2 = u_1 v_2 - u_2 v_1$ . Expanding both sides using algebraic expansion yields the desired result.

—Joel Kindiak, 21 Mar 25, 1426H

September 29, 2025
Euler’s Handy Formula

Use Euler’s formula in this question without proof.

Theorem 1 (Euler’s Formula). For any $t \in \mathbb R$ ,

$e^{it} = \cos(t) + i \sin(t).$

Remark 1. Setting $t = \pi$ yields Euler’s famous identity $e^{i \pi} + 1 = 0$ .

Problem 1. Let 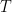$T$ be a linear transformation. Prove that

$\begin{aligned} T(\cos(t)) &= \frac 12 (T(e^{it}) + T(e^{-it})), \\ T(\sin(t)) &= \frac 1{2i} (T(e^{it}) - T(e^{-it})). \end{aligned}$

(Click for Solution)

Solution. By Euler’s formula,

$\begin{aligned} e^{it} &= \cos(t) + i \sin(t), \\ e^{-it} &= \cos(t) - i \sin(t). \end{aligned}$

Adding (resp. subtracting) then dividing by 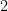$2$ (resp. 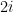$2i$ ) yields

$\displaystyle \cos(t) = \frac{e^{it} + e^{-it}}{2},\quad \sin(t) = \frac{e^{it} + e^{-it}}{2i}.$

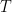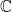The result follows since $T$ is linear over $\mathbb C$ .

Let $p$ be any polynomial and $\alpha \in \mathbb C$ be a constant. Define the linear transformation $\displaystyle \frac 1{p(\mathcal D)}$ by

$\displaystyle \frac 1{p(\mathcal D)}(e^{\alpha t} \cdot V(t)) := e^{\alpha t} \cdot \frac 1{p(\mathcal D + \alpha)} (V(t)).$

Furthermore, define $\displaystyle \frac 1{p(\mathcal D)}(1) := \frac 1{p(0)}$ if $p(0) \neq 0$ and $\displaystyle \frac 1{\mathcal D}(1) := t$ .

Problem 2. For any polynomial 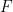$F$ such that $F(\alpha) \neq 0$ , evaluate $\displaystyle \frac 1{F(\mathcal D)}(e^{\alpha x})$ .

(Click for Solution)

Solution. By the given result using $V(x) = 1$ ,

$\displaystyle \frac 1{p(\mathcal D)}(e^{\alpha t} \cdot 1) = e^{\alpha t} \cdot \frac 1{p(\mathcal D + \alpha)} (1).$

Defining the polynomial $q$ by $q(x) := p(x+\alpha)$ , we have $q(0) = p(\alpha) \neq 0$ , so that the right-hand side simplifies to

$\displaystyle \frac 1{p(\mathcal D)}(e^{\alpha t}) = e^{\alpha t} \frac 1{q(\mathcal D)} (1) = e^{\alpha t} \cdot \frac 1{q(0)} = e^{\alpha t} \cdot\frac 1{p(\alpha)} = \frac 1{p(\alpha)} \cdot e^{\alpha t}.$

Problem 3. For any polynomial 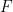$F$ such that $F(-k^2) \neq 0$ , evaluate $\displaystyle \frac 1{F(\mathcal D^2)}(\cos kt)$ and $\displaystyle \frac 1{F(\mathcal D^2)}(\sin kt)$ .

(Click for Solution)

Solution. By Problem 1,

$\begin{aligned} \frac 1{F(\mathcal D^2)}(\cos kt) &= \frac 12 \cdot \left( \frac 1{F(\mathcal D^2)} (e^{(ik)t}) + \frac 1{F(\mathcal D^2)} (e^{(-ik)t}) \right) \\ &= \frac 12 \cdot \left( \frac 1{G(\mathcal D)} (e^{(ik)t}) + \frac 1{G(\mathcal D)} (e^{(-ik)t}) \right) \end{aligned}$

where we defined the polynomial $G$ by $G(x) := F(x^2)$ . We observe that

$G(\pm ik) = F((\pm ik)^2) = F((ik)^2) = F(i^2 \cdot k^2) = F(-k^2) \neq 0.$

By Problem 2,

$\begin{aligned} \frac 1{F(\mathcal D^2)}(\cos kt) &= \frac 12 \cdot \left( \frac 1{G(\mathcal D)} (e^{(ik)t}) + \frac 1{G(\mathcal D)} (e^{(-ik)t}) \right) \\ &= \frac 12 \cdot \left( \frac 1{G(ik)} (e^{(ik)t}) + \frac 1{G(-ik)} (e^{(-ik)t}) \right) \\ &= \frac 12 \cdot \left( \frac 1{F(-k^2)} (e^{(ik)t}) + \frac 1{F(-k^2)} (e^{(-ik)t}) \right) \\ &= \frac 1{F(-k^2)} \left(\frac {e^{i(kt)} + e^{-i(kt)}}{2} \right) = \frac 1{F(-k^2)} \cos(kt). \end{aligned}$

In an analogous manner, $\displaystyle \frac 1{F(D^2)}(\sin kt) = \frac 1{F(-k^2)} \sin(kt)$ .

Problem 4. Evaluate $\displaystyle \frac 1{\mathcal D^2 + k^2}(\cos kt)$ and $\displaystyle \frac 1{\mathcal D^2 + k^2}(\sin kt)$ .

(Click for Solution)

Solution. We will take advantage of the factorisation $z^2 + k^2 = (z-ik)(z+ik)$ . We observe that

$\begin{aligned} \frac{1}{\mathcal D^2 + k^2}(e^{ikt}) &= \frac{1}{(\mathcal D - ik)(\mathcal D + ik)}(e^{ikt}) \\ &= \frac{1}{\mathcal D - ik}\left( \frac{1}{\mathcal D + ik} (e^{ikt}) \right) \\ &= \frac{1}{\mathcal D - ik} \left( \frac{1}{ik + ik} (e^{ikt}) \right) \\ &= \frac 1{2ik} \cdot \frac{1}{\mathcal D - ik} (e^{ikt}) \\ &= \frac 1{2ik} \cdot e^{ikt} \cdot \frac{1}{(\mathcal D + ik) - ik} (1) \\ &= \frac 1{2ik} \cdot e^{ikt} \cdot \frac{1}{\mathcal D}(1) = \frac 1{2ik} te^{ikt}. \end{aligned}$

Similarly, $\displaystyle \frac{1}{\mathcal D^2 + k^2}(e^{-ikt}) = -\frac 1{2ik} te^{-ikt}$ . By Problem 1,

$\begin{aligned} \frac{1}{\mathcal D^2 + k^2}(\cos kt) &= \frac 12 \cdot \left(\frac{1}{\mathcal D^2 + k^2}(e^{ikt}) + \frac{1}{\mathcal D^2 + k^2}(e^{-ikt}) \right) \\ &= \frac 12 \cdot \left( \frac 1{2ik} te^{ikt} -\frac 1{2ik} te^{-ikt} \right) \\ &= \frac {t}{2k} \cdot \left( \frac {e^{ikt} - e^{-ikt}}{2i} \right) = \frac {t \sin kt}{2k}.\end{aligned}$

Analogously, $\displaystyle \frac{1}{\mathcal D^2 + k^2}(\sin kt) = -\frac {t \cos kt}{2k}$ .

Problem 5. Suppose $\mathcal L$ is a linear transformation such that for any constant $\alpha \in \mathbb C$ ,

$\displaystyle \mathcal L \{e^{\alpha t} \} = \frac 1{s-\alpha }.$

For any constant $a \in \mathbb R$ , evaluate the real-valued functions $\mathcal L \{\cos(at)\}$ and $\mathcal L \{\sin(at)\}$ .

(Click for Solution)

Solution. Replacing $\alpha$ with $i a$ ,

$\begin{aligned}\mathcal L \{e^{i a t} \} = \frac 1{s-ia} &= \frac {s+ia}{(s-ia)(s+ia) } \\ &= \frac{s+ia}{s^2 + a^2} = \frac{s}{s^2 + a^2} + i \cdot \frac{a}{s^2 + a^2}. \end{aligned}$

By Euler’s formula and the linearity of $\mathcal L$ ,

$\mathcal L \{ e^{i a t} \} = \mathcal L\{ \cos(at) \} + i \cdot \mathcal L\{ \sin(at)\}$

Hence,

$\displaystyle \mathcal L\{ \cos(at) \} + i \cdot \mathcal L\{ \sin(at)\} = \frac{s}{s^2 + a^2} + i \cdot \frac{a}{s^2 + a^2}.$

Comparing real and imaginary parts,

$\displaystyle \mathcal L \{ \cos(at) \} = \frac{s}{s^2 + a^2},\quad \mathcal L\{ \sin(at) \} = \frac{a}{s^2 + a^2}.$

Remark 2. One can explore the feasibility of these definitions for trigonometric functions defined using complex arguments:

$\displaystyle \cos(z) = \frac{e^{iz} + e^{-iz}}{2},\quad \sin(z) = \frac{e^{iz} - e^{-iz}}{2i}.$

I haven’t done so, so perhaps that’s an open question.

—Joel Kindiak, 19 May 25, 2113H

May 19, 2025
Create Your Own Vector Space
Problem 1. Let $V$ be a vector space over a field $\mathbb K$ . For any set $K$ , suppose there exists a bijection $T : K \to V$ . Prove that $K$ can be equipped with addition and scalar multiplication operations such that $K$ becomes a vector space over $\mathbb K$ .

(Click for Solution)

Solution. The key idea is to define the addition and scalar multiplication operators in $V$ , and then transport them back to $K$ . Define

$x + y := T^{-1}(T(x) + T(y)),\quad c \cdot x := T^{-1}(cT(x)).$

Since $T$ is bijective, the operations are well-defined. The additive identity will be $T^{-1}(\mathbf 0)$ , since

$\begin{aligned} x + T^{-1}(\mathbf 0) &= T^{-1}(T(x) + T(T^{-1}(\mathbf 0))) \\ &= T^{-1}(T(x) + \mathbf 0) \\ &= T^{-1}(T(x)) = x.\end{aligned}$

For any $x \in K$ , and the additive inverse will be $T^{-1}(-T(x))$ , since

$\begin{aligned}x + T^{-1}(-T(x)) &= T^{-1}(T(x) + T(T^{-1}(-T(x)))\\ &= T^{-1}(T(x) + (-T(x)) \\ &= T^{-1}(\mathbf 0). \end{aligned}$

We leave it as an exercise to verify the rest of the vector space axioms.

Remark. These definitions turn $T$ into a linear transformation from $K$ to $V$ .

Problem 2. Let $V$ be a vector space over $\mathbb K$ . Prove the following properties:
- Suppose $\mathbf u \in V$ has the following property: For any $\mathbf v$ , $\mathbf v + \mathbf u = \mathbf v$ . Then $\mathbf u = \mathbf 0$ .
- Fix $\mathbf v \in V$ . If $\mathbf u \in V$ has the property that $\mathbf v + \mathbf u = \mathbf 0$ , then $\mathbf u = -\mathbf v$ .
- For any $\mathbf v \in V$ , $0\mathbf v = \mathbf 0$ .
- For any $\mathbf v \in V$ , $(-1)\mathbf v = -\mathbf v$ .
(Click for Solution)

Solution. For the first property, consider $\mathbf v = \mathbf 0$ . Then

$\mathbf u = \mathbf 0 + \mathbf u = \mathbf 0.$

For the second property, adding $-\mathbf v$ on both sides yields

$\begin{aligned}-\mathbf v + (\mathbf v + \mathbf u) &= -\mathbf v + \mathbf 0 \\ (-\mathbf v + \mathbf v) + \mathbf u &= -\mathbf v \\ \mathbf 0 + \mathbf u &= -\mathbf v \\ \mathbf u &= -\mathbf v,\end{aligned}$

where each equation implies the next. For the third property, use the property $0 + 0 = 0$ to obtain

$\begin{aligned}(0 + 0) \mathbf v &= 0\mathbf v \\ 0 \mathbf v + 0 \mathbf v &= 0 \mathbf v \\ -0 \mathbf v + (0 \mathbf v + 0 \mathbf v ) &= -0 \mathbf v + 0 \mathbf v \\ (-0 \mathbf v + 0 \mathbf v) + 0 \mathbf v &= -0 \mathbf v + 0 \mathbf v \\ \mathbf 0 + 0 \mathbf v &= \mathbf 0 \\ 0 \mathbf v &= \mathbf 0,\end{aligned}$

where each equation implies the next. For the fourth property, use the property $1 + (-1) = 0$ to obtain

$\begin{aligned} \mathbf 0 &= 0 \mathbf v \\ \mathbf 0 &= (1 + (-1))\mathbf v \\ \mathbf 0 &= \mathbf v + (-1)\mathbf v \\ -\mathbf v + \mathbf 0 &= -\mathbf v + (\mathbf v + (-1)\mathbf v ) \\ -\mathbf v + \mathbf 0 &= (-\mathbf v + \mathbf v) + (-1)\mathbf v \\ -\mathbf v &= \mathbf 0 + (-1)\mathbf v \\ -\mathbf v &= (-1)\mathbf v,\end{aligned}$

where each equation implies the next.

—Joel Kindiak, 27 Feb 25, 2355H
April 14, 2025
A Surprising Determinant

Problem 1. Let $\mathbf{A}$ be a real square matrix. Suppose $\mathbf{A} \mathbf{A}^{\mathrm T} = \mathbf{I}$ and $\det(\mathbf{A}) < 0$ . Compute $\det(\mathbf{A} + \mathbf{I})$ .

(Click for Solution)

Solution. Since $\mathbf{A}\mathbf{A}^{\mathrm T} = \mathbf{I}$ , we have

$\begin{aligned} \mathbf{A} + \mathbf{I} &= \mathbf{A} + \mathbf{A}\mathbf{A}^{\mathrm T} \\ &= \mathbf{A}(\mathbf{I} + \mathbf{A}^{\mathrm T}) \\ &= \mathbf{A}(\mathbf{A} + \mathbf{I}^{\mathrm T}) \\ &= \mathbf{A}(\mathbf{A}^{\mathrm T} + \mathbf{I}^{\mathrm T}) \\ &= \mathbf{A}(\mathbf{A} + \mathbf{I})^{\mathrm T}. \end{aligned}$

Taking determinants on both sides,

$\begin{aligned} \det(\mathbf{A} + \mathbf{I}) &= \det (\mathbf{A} (\mathbf{A} + \mathbf{I})^{\mathrm T}) \\ &= \det (\mathbf{A}) \det((\mathbf{A} + \mathbf{I})^{\mathrm T}) \\ &= \det (\mathbf{A}) \det(\mathbf{A} + \mathbf{I}). \end{aligned}$

Therefore, $\det(\mathbf{A} + \mathbf{I}) ( 1 - \det(\mathbf{A}) ) = 0$ . Since $\det(\mathbf{A}) < 0$ , we have

$1 - \det(\mathbf{A}) > 1 - 0 = 1 > 0 \quad \Rightarrow \quad \det(\mathbf{A} + \mathbf{I}) = 0.$

—Joel Kindiak, 9 Feb 25, 1322H

March 25, 2025
Reversing Linear Transformations

Throughout this post, let $V,W$ be vector spaces over some field $\mathbb F$ and $T : V \to W$ be a linear transformation.

Problem 1. For any subspace $K \subseteq V$ , prove that $T(K)$ is a subspace of $W$ . In particular, the range $T(V)$ of $T$ is a subspace of $W$ .

(Click for Solution)

Solution. For any $x,y \in K$ and for any scalar $c \in \mathbb F$ ,

$T(x) + T(y) = T(x+y) \in T(K),\quad cT(x) = T(cx) \in T(K).$

Problem 2. For any subspace $L \subseteq W$ , prove that $T^{-1}(L)$ is a subspace of $V$ . In particular, the kernel $\mathrm{ker}(T):= T^{-1}(\{0\})$ of $T$ is a subspace of $V$ .

(Click for Solution)

Solution. For any $x,y \in T^{-1}(L)$ , $T(x),T(y) \in K$ . Since $K$ is a subspace of $W$ , for any scalar $c \in \mathbb F$ ,

$T(x+y) = T(x) + T(y) \in L,\quad T(cx) = cT(x) \in L.$

Problem 3. For any $x, y \in V$ , prove that $T(x) = T(y)$ if and only if $x-y \in \mathrm{ker}(T)$ .

(Click for Solution)

Solution. We have $T(x) = T(y) \iff T(x) - T(y) = 0 \iff T(x-y) = 0$ .

Problem 4. For subspaces $K_1, K_2 \subseteq W$ , prove that

$K_1 +K_2 := \{x + y : x \in K_1, y \in K_2\}$

is a subspace of $W$ . Also, for any $c \in \mathbb F$ , prove that $cK_1 := \{cx : x \in K_1\}$ is a subspace of $W$ .

(Click for Solution)

Solution. For any $x_1+y_1, x_2+y_2 \in K_1 + K_2$ ,

$(x_1+y_1) + (x_2+y_2) = (x_1 + x_2) + (y_1 + y_2) \in K_1 + K_2.$

Similarly, for any scalar $c \in \mathbb F$ ,

$c(x_1+y_1) = c x_1 + c x_2 \in K_1 + K_2.$

The proof for $cK_1$ is similar.

Problem 5. For subspaces $K_1, K_2 \subseteq W$ , prove that

$T^{-1}(K_1 + K_2) \supseteq T^{-1}(K_1) + T^{-1}(K_2) + \mathrm{ker}(T),$

where equality holds if $T$ is surjective.

(Click for Solution)

Solution. For the first claim, to prove $(\supseteq)$ , we note that for any $x_i \in T^{-1}(K_i)$ , $x_3 \in \mathrm{ker}(T)$ ,

$T(x_1+x_2+x_3) = T(x_1) + T(x_2) \in K_1 + K_2$

so that $x_1+x_2+x_3 \in T^{-1}(K_1 + K_2)$ .

To prove $(\subseteq)$ when $T$ is surjective, fix $x \in T^{-1}(K_1 + K_2)$ . Then $T(x) \in K_1 + K_2$ . Hence, there exists $y_i \in K_i$ such that $T(x) = y_1 + y_2$ .

Since $T$ is surjective, find $x_i \in V$ such that $T(x_i) = y_i \in K_i \Rightarrow x_i \in T^{-1}(K_i)$ . Then $T(x) = T(x_1) + T(x_2) = T(x_1 + x_2)$ . By Problem 3,

$x_3 := x - (x_1 + x_2) \in \mathrm{ker}(T).$

Hence, $x = x_1 + x_2 + x_3 \in T^{-1}(K_1) + T^{-1}(K_2) + \mathrm{ker}(T)$ .

Problem 6. For any scalar $c \in \mathbb F$ and subspace $K \subseteq W$ , prove that $T^{-1}(cK_1) = c T^{-1}(K_1)$ .

(Click for Solution)

Solution. We make the quick observation that

$\displaystyle x \in K \quad \iff \quad cx \in cK,$

for any vector subspace $K$ . This means for any $x \in K_1$ ,

$T(x) \in cK_1 \quad \iff \quad T(c^{-1} x) \in K_1,$

where $c^{-1} := 1/c$ for brevity. The result follows by bookkeeping.

—Joel Kindiak, 26 Jan 25, 1826H

January 31, 2025
A Shocking Trichotomy

Problem 1. Let $V$ be a vector space over $\mathbb R$ . Prove that if $V$ has at least one nonzero element, then $V$ has infinitely many elements.

(Click for Solution)

Solution. Suppose $V$ contains some nonzero $v$ . Since $V$ is a vector space over $\mathbb R$ , $V$ contains $tv$ for any $t \in \mathbb R$ . Each $t$ yields a unique $tv$ since $v \neq 0$ . Thus, $V$ contains an infinite number of elements given by the injection $\mathbb R \to V, t \mapsto tv$ .

Problem 2. Let $V, W$ be a vector spaces over $\mathbb R$ , and $T : V \to W$ be a linear transformation. For any $y \in W$ , prove that the equation $T(x) = y$ either has zero solutions, or one solution, or infinitely many solutions.

(Click for Solution)

Solution. If the equation $T(x) = y$ has no solutions, then we are done. Otherwise, it has at least one solution $u$ , which yields $T(u) = y$ .

If the equation has at most one solution, then we are done. Otherwise, the equation has at least one other solution $v \neq u$ , which yields $T(v) = y$ . Since $T$ is linear,

$T(v-u) = T(v) - T(u) = y - y = 0.$

For any $t \in \mathbb R$ , consider the vector $x_t := u + t(v-u)$ . Each $t$ yields a unique $x_t$ since $v-u \neq 0$ . On the other hand

$\begin{aligned} T(x_t) &= T(u + t(v-u)) \\ &= T(u) + t \cdot T(v-u) \\ &= y + t \cdot 0 \\ &= y + 0 = y. \end{aligned}$

Thus, the equation $T(x)=y$ has infinitely many solutions defined by $x_t = u + t(v-u)$ .

—Joel Kindiak, 30 Nov 24, 0112H

December 13, 2024
Equating Ranges and Kernels

Problem 1. Let $V$ be a vector space and $T : V \to V$ be a linear transformation. Suppose $T^2 = I$ , where we denote $I = I_V$ for brevity. Prove that $(T-I)(V) = \mathrm{ker}(T+I)$ .

(Click for Solution)

Solution. Under the hypothesis that $T^2 = I$ , we have $(T+I)(T-I) = O$ .

We will first prove $(\subseteq)$ . Fix $v \in (T-I)(V)$ . Find $w \in V$ such that $v = (T-I)(w)$ . Then

$(T+I)(v) = (T+I)(T-I)(w) = (T^2 - I)(w) = O(w) = 0,$

so that $v \in \mathrm{ker}(T+I)$ . Hence, $(T-I)(V) \subseteq \mathrm{ker}(T+I)$ .

Now, we prove $(\supseteq)$ . Fix $v \in \mathrm{ker}(T+I)$ . Then

$0 = (T+I)(v) = T(v) + v \quad \Rightarrow \quad v = -T(v) = T(-v).$

By repeated application of this result,

$v = \frac 12v + \frac 12v = T(-\frac 12 v) - (-\frac 12 v) = (T-I)(-\frac 12 v) \in (T-I)(V).$

Hence, $\mathrm{ker}(T+I) \subseteq (T-I)(V)$ .

Combining both results, $(T-I)(V) = \mathrm{ker}(T+I)$ .

—Joel Kindiak, 29 Nov 24, 2130H

December 6, 2024
A Unitarily Normal Problem

I couldn’t solve this linear algebra question as an undergraduate. Today, we revisit it and defeat it once and for all.

Problem 1. Let $V$ be a finite-dimensional (complex) vector space equipped with the inner product $\langle \cdot, \cdot \rangle$ . Let $T$ be an invertible linear operator. Suppose that for any $u,v \in V$ ,

$\displaystyle \frac{\langle T(u), T(v)\rangle}{\sqrt{\langle T(u), T(u) \rangle \langle T(v), T(v) \rangle}} = \frac{\langle u, v\rangle}{\sqrt{\langle u, u \rangle \langle v, v \rangle}}.$

Prove that $T$ is a scalar multiple of some unitary operator.

It is not hard to show that the converse holds (i.e. if $T$ is a scalar multiple of a unitary operator then the equation holds).

In the original exam paper, the examiner actually offered sub-steps to the question. The solution will therefore follow the suggested roadmap and furthermore, address the result more directly.

(Click for Solution)

Solution. We first observe that $(T^* \circ T)^* = T^* \circ T$ implies that $T^* \circ T$ is self-adjoint, therefore normal, and thus unitarily diagonalisable.

Thus, there exists an orthonormal basis $B := \{v_1,\dots,v_n\}$ for $V$ such that $(T^* \circ T)v_i = \lambda_i v_i$ , where each $\lambda_i \in \mathbb{C}$ .

We observe that

$\langle T(v_i),T(v) \rangle = \langle (T^* \circ T)(v_i),v \rangle = \langle \lambda_i v_i,v \rangle = \lambda_i \langle v_i,v \rangle.$

In particular,

${\| T(v_i) \|}^2 = \langle T(v_i),T(v_i) \rangle = \lambda_i \langle v_i,v_i \rangle = \lambda_i$

so that $\lambda_i > 0$ . Thus, substituting $u = v_i$ into the equation

$\displaystyle \frac{\langle T(u), T(v)\rangle}{\| T(u)\| \| T(v) \|} = \frac{\langle u, v\rangle}{\| u \| \| v \|}$

and simplifying,

$\displaystyle \frac{ \lambda_i \langle v_i,v \rangle}{ \sqrt{\lambda_i} \| T(v) \| } = \frac{\langle v_i, v\rangle}{\| v \|}.$

Simplifying for any $v \in V$ such that $\langle v_i, v\rangle \neq 0$ ,

$\displaystyle \| T(v) \| = \sqrt{\lambda_i} \| v\|.$

Since $\lambda_i$ was chosen arbitrarily, we must have $\lambda_1 = \cdots = \lambda_n = \lambda$ so that

$\displaystyle \| T(v) \| = \sqrt{\lambda} \| v\|\quad \iff \quad \left\|\left( \frac T{\sqrt{\lambda}} \right) v \right\| = \|v\|.$

It is not hard to show that this equation holds for any $v \in V$ . Thus, $S:=(1/\sqrt{\lambda})T$ is unitary, and $T = \sqrt{\lambda} S$ , as required.

—Joel Kindiak, 19 Oct 24, 0150H

October 19, 2024