Last time, we discussed symmetric bilinear forms and its applications into geometry, in particular, to rational trigonometry, which posits a computationally tractable alternative to classical trigonometry. The rational analog of distance  would be the quadrance
would be the quadrance 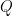 , and the rational analog of angle
, and the rational analog of angle 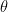 would be the spread
would be the spread  , connected in the case
, connected in the case  by the equations
by the equations

In this post, we see how we can use linear algebra and ideas in rational trigonometry to define a broad framework for geometry, of which we obtain Euclid’s five postulates in the special case  .
.
Let 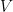 be a vector space over a field
be a vector space over a field  .
.
Definition 1. An affine space  over
over 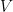 is a set
is a set  , whose elements are called points, equipped with an addition map
, whose elements are called points, equipped with an addition map  that satisfies the following properties:
that satisfies the following properties:
- For any
 ,
,  .
.
- For any
 and
and  ,
,  .
.
- For any
 , the map
, the map  is bijective.
is bijective.
Example 1. Any vector space 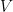 is an affine space over itself. Defining
is an affine space over itself. Defining  , for each point
, for each point  in
in  , we will define the position vector
, we will define the position vector  .
.
Lemma 1. For points  , there exists a unique vector
, there exists a unique vector  such that
such that  .
.
Proof. Fix  . Since
. Since  is bijective, there exists a unique vector
is bijective, there exists a unique vector  such that
such that  . Denote
. Denote  .
.
Hence, we will denote  without loss of ambiguity.
without loss of ambiguity.
Lemma 2. For points  ,
,  precisely when
precisely when  and
and  .
.
Henceforth, let  denote any affine space over
denote any affine space over 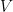 . Therefore, points are positions determined by vectors that start from the origin. Each point
. Therefore, points are positions determined by vectors that start from the origin. Each point  can be described by a position vector
can be described by a position vector  . Let
. Let  be any field that contains
be any field that contains  .
.
Definition 1. A line  containing the point
containing the point  and parallel to the vector
and parallel to the vector  is the set
is the set

Equivalently, we say that  belongs in the line if its position vector
belongs in the line if its position vector  satisfies the parametric equation of a line, i.e.
satisfies the parametric equation of a line, i.e.  .
.
Theorem 1. For any two distinct points  , there exists a unique line that contains
, there exists a unique line that contains  and
and  .
.
Proof. For existence, define the line  by the equation
by the equation  . Since
. Since  and
and  ,
, 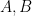 lie on
lie on  .
.
For uniqueness, let  be any other line that passes through
be any other line that passes through 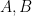 . Then there exists a point
. Then there exists a point  and a vector
and a vector  such that
such that  . Find distinct scalars
. Find distinct scalars  such that
such that  and
and  . Then
. Then

We need to prove that  . For any
. For any  , find
, find  such that
such that

Hence,  . We can prove
. We can prove  similarly since
similarly since

In particular, when  and
and  , we obtain Euclid’s first two postulates:
, we obtain Euclid’s first two postulates:
Corollary 1. A straight line segment can be drawn joining any two points. Furthermore, any straight line segment can be extended indefinitely in a straight line.
The rest of Euclid’s postulates will require our previous discussion on symmetric bilinear forms ![[ \cdot , \cdot ]](https://s0.wp.com/latex.php?latex=%5B+%5Ccdot+%2C+%5Ccdot+%5D&bg=ffffff&fg=000&s=0&c=20201002) , which basically characterise perpendicularity, since the usual inner product
, which basically characterise perpendicularity, since the usual inner product  on
on  yields the desired properties.
yields the desired properties.
Recall that for any symmetric bilinear form ![[ \cdot , \cdot ] : V \times V \to \mathbb K](https://s0.wp.com/latex.php?latex=%5B+%5Ccdot+%2C+%5Ccdot+%5D+%3A+V+%5Ctimes+V+%5Cto+%5Cmathbb+K&bg=ffffff&fg=000&s=0&c=20201002) , we can define the quadrance
, we can define the quadrance  by
by ![Q(\mathbf v) = [ \mathbf v , \mathbf v ]](https://s0.wp.com/latex.php?latex=Q%28%5Cmathbf+v%29+%3D+%5B+%5Cmathbf+v+%2C+%5Cmathbf+v+%5D&bg=ffffff&fg=000&s=0&c=20201002) . In particular, for points
. In particular, for points  , we can define the quadrance between two points
, we can define the quadrance between two points  by
by  .
.
Definition 3. A sphere  with centre
with centre 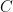 and quadrance
and quadrance 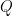 is defined to be the set
is defined to be the set

A sphere in  equipped with the usual inner product is called a circle.
equipped with the usual inner product is called a circle.
Theorem 2. For any two distinct points  , there exists a unique circle with centre
, there exists a unique circle with centre  and quadrance
and quadrance  .
.
Corollary 2. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
Definition 4. For  , we say that
, we say that  and
and  are perpendicular or orthogonal, denoted
are perpendicular or orthogonal, denoted  , if
, if ![[\mathbf u, \mathbf v] = 0](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf+u%2C+%5Cmathbf+v%5D+%3D+0&bg=ffffff&fg=000&s=0&c=20201002) .
.
Lemma 3. If  have nonzero quadrances, then
have nonzero quadrances, then  .
.
Theorem 3. All right angles are congruent to one another.
We are left with the infamous parallel postulate, which seems nontrivial to state, but turns out to be definable using the notions we discussed in affine spaces. We remark that to debunk the parallel postulate, we will need a broader notion of space, possibly projective space, to account for the varied notions of parallelism.
Definition 5. Two nonzero vectors  are parallel, denoted
are parallel, denoted  , if the set
, if the set  is linearly dependent i.e. there exists some
is linearly dependent i.e. there exists some  such that
such that  . We say that the lines
. We say that the lines  and
and  are parallel if
are parallel if  .
.
Theorem 4. For any line  and point
and point  , there exists at most one line passing through
, there exists at most one line passing through  that is parallel to
that is parallel to  .
.
Proof. Let  and
and  be lines that pass through
be lines that pass through  and are parallel to
and are parallel to  . Let
. Let  be points on
be points on  and define
and define  . For any point
. For any point  on
on  ,
,  . Likewise, for any point
. Likewise, for any point  on
on  ,
,  . Thus,
. Thus,  . Some bookkeeping yields
. Some bookkeeping yields  .
.
Corollary 3 (Playfair’s Axiom). In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.
Corollary 4. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
Proof. Corollary 3 implies Corollary 4 via the following geometric argument, which only requires Corollary 1 and Corollary 2 to establish.
With that, we have successfully created a working model for Euclidean geometry, defining quadrances and spreads in general fields, then take square roots in the case  and even employing trigonometric functions to obtain our classical notions of distances and angles (in radians). We now list three common starting points for elementary school students’ learning of Euclidean geometry.
and even employing trigonometric functions to obtain our classical notions of distances and angles (in radians). We now list three common starting points for elementary school students’ learning of Euclidean geometry.
Corollary 5. Define  so that
so that  . The following proposition holds:
. The following proposition holds:
- Adjacent angles on a straight line sum to
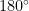 .
.
- Interior angles on the same side of a transversal sum to
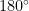 .
.
Interestingly, we do not have purely mechanistic tools to draw an angle of  , but can define the concept mathematically and obtain close approximations to that. However, using constructions in Euclidean geometry, we can draw the obvious angle
, but can define the concept mathematically and obtain close approximations to that. However, using constructions in Euclidean geometry, we can draw the obvious angle  and the special angle
and the special angle  , bisections of these angles, sums and differences, and integer multiples of said angles.
, bisections of these angles, sums and differences, and integer multiples of said angles.
In the next post, we take advantage of inner product spaces to discuss orthogonal functions, and derive the usual formulas involved in discussing Fourier series.
—Joel Kindiak, 20 Mar 25, 1523H
can be diagonalised in a generalised sense into the Jordan normal form.
or
can be diagonalised. In a modified sense, of course. This is called singular value decomposition.
, there exist unitary matrices
and
and a diagonal matrix
such that
is diagonal to mean that
whenever
.
is unitarily diagonalisable with nonnegative eigenvalues.
is self-adjoint, and thus normal. By the spectral theorems, it is unitarily diagonalisable, i.e. there exists an orthonormal basis of
consisting of eigenvectors of
.
. Then
,
and
be matrices.
.
.
.
.
. By orthogonal decomposition,
and
. The third result follows from the containment
and
in the fourth result is an obvious corollary. For the direction
, we leave it as an exercise to verify that
, from which the result follows by the rank-nullity theorem.
for
, if
is any orthonormal basis for
and
is any orthonormal basis for
, defining
,
and
, as well as suitably defined numbers
such that
. By Lemma 1, the matrix
is unitarily diagonalisable with nonnegative eigenvalues
. Furthermore, for
,
is orthogonal, and for each
,
. Define the corresponding unit vectors
is clearly orthonormal. Extend it to an orthonormal basis for
via a modified form of the Gram-Schmidt process to yield the desired result.
are called the singular values of
.