Skip to content

KindiakMath

About
- Curriculum Vitae
- Review Quotes
Pre-University
Foundational Math
Theoretical Analysis
Unified Math
- Complex Analysis
- Abstract Algebra
Para-Mathematics

Category: Exercises

Jordan Decomposition
This post is inspired by Professor Tom Fischer’s writeup.

Recall the Hahn decomposition theorem:

Theorem 1. If $\mu$ is a signed measure on $(\Omega, \mathcal F)$ , then there exist disjoint measurable subsets $P, N \in \mathcal F$ such that

$\mu (\cdot \cap P) \in [0, \infty),\quad \mu (\cdot \cap N) \in (-\infty, 0] ,\quad P \sqcup N = \Omega.$

We call $P$ a positive set, denoted $P \geq 0$ , and $N$ a negative set, denoted $N \leq 0$ , and we call the pair $(P, Q)$ a Hahn decomposition for $\mu$ .

Call a set $M$ is $\mu$ –null if it is positive and negative: $\mu( \cdot \cap M) \in \{0\}$ .

Define the symmetric difference by

$K\triangle L := (K \backslash L) \sqcup (L \backslash K).$

We leave it as an exercise to verify that

$K \cup L = (K \cap L) \sqcup (K\triangle L).$

Problem 1. Let $\mu$ be a signed measure on $(\Omega, \mathcal F)$ and $(P_1,N_1)$ , $(P_2,N_2)$ be two Hahn decompositions for $\mu$ . Show that $P_1 \triangle P_2$ and $N_1 \triangle N_2$ are $\mu$ -null.

(Click for Solution)

Solution. Fix $K \in \mathcal F$ . Then

$\begin{aligned} \mu(K \cap (P_1 \triangle P_2)) &= \mu(K \cap P_1 \backslash P_2) + \mu(K \cap P_2 \backslash P_1) \\ &= \mu(K \cap P_1 \cap N_2) + \mu(K \cap P_2 \cap N_2) \\ &= \mu(K \cap P_1 \cap N_2) + \mu(\emptyset) \\ &= \mu(K \cap P_1 \cap N_2). \end{aligned}$

Using Theorem 1,

$\begin{aligned} 0 &\leq \mu((K \cap N_2) \cap P_1) \\ &= \mu(K \cap P_1 \cap N_2) \\ &= \mu((K \cap P_1) \cap N_2) \leq 0, \end{aligned}$

so $\mu(K \cap (P_1 \triangle P_2)) = \mu(K \cap P_1 \cap N_2) = 0$ , as required.

We now state the Jordan decomposition theorem.

Problem 2. Let $\mu$ be a finite signed measure on $(\Omega, \mathcal F)$ . Construct unique finite measures $\mu^+, \mu^-$ on $(\Omega , \mathcal F)$ such that:
- $\mu = \mu^+ - \mu^-$ , and
- for any Hahn decomposition $(P, N)$ of $(\Omega, \mathcal F)$ , $\mu^+(K) = 0$ for $K \subseteq N$ and $\mu^-(K) = 0$ for $K \subseteq P$ .
We call $(\mu^+, \mu^-)$ the (unique) Jordan decomposition of $\mu$ .

(Click for Solution)

Solution. Use Theorem 1 to construct a Hahn decomposition $(P_1, N_1)$ . Define

$\begin{aligned} \mu^+ &:= \mu(\cdot \cap P_1) \in [0, \infty),\\ \mu^- &:= -\mu(\cdot \cap N_1) \in [0, \infty). \end{aligned}$

Then for any $K \in \mathcal F$ ,

$\begin{aligned} \mu(K) &= \mu(K \cap P_1) + \mu(K \cap N_1) \\ &= \mu^+(K) - \mu^-(K) \\ &= (\mu^+ - \mu^-)(K). \end{aligned}$

Hence, $\mu = \mu^+ - \mu^-$ .

Now fix any Hahn decomposition $(P_2, N_2)$ . Then

$\begin{aligned} P_1 &= P_1 \cap (P_1 \cup P_2) \\ &= P_1 \cap ((P_1 \cap P_2) \sqcup (P_1 \triangle P_2)) \\ &= (P_1 \cap (P_1 \cap P_2)) \sqcup (P_1 \cap (P_1 \triangle P_2)) \\ &= (P_1 \cap P_2) \sqcup (P_1 \cap (P_1 \triangle P_2)).\end{aligned}$

Fix $K \subseteq N_2$ . Then

$\begin{aligned} \mu^+(K) &= \mu(K \cap P_1) \\ &= \mu(K \cap P_1 \cap P_2) + \mu(K \cap P_1 \cap (P_1 \triangle P_2)) \\ &= \mu(K \cap \emptyset) + \mu((K \cap P_1) \cap (P_1 \triangle P_2)) \\ &= 0 + 0 = 0. \end{aligned}$

Similarly, $K \subseteq P_2$ implies $\mu^-(K) = 0$ .

Finally, we establish the uniqueness of the measures. Suppose

$\mu = \mu_1^+ - \mu_1^- = \mu_2^+ - \mu_2^-.$

We need to check that $\mu_1^+ = \mu_2^+$ . To that end, fix any Hahn decomposition $(P, N)$ . For any $K \subseteq P$ ,

$\mu_1^+(K \cap N) = 0 = \mu_2^+(K \cap N)$

and

$\mu_1^-(K) = 0 = \mu_2^-(K)$

so that

$\begin{aligned} \mu_1^+(K) &= \mu(P) - \mu_1^-(K) \\ &= \mu(P) - \mu_2^-(K) = \mu_2^+(K). \end{aligned}$

Hence, for any $K = (K \cap P) \sqcup (K \cap N)$ ,

$\begin{aligned} \mu_1^+(K) &= \mu_1^+(K \cap P) + \mu_1^+(K \cap N) \\ &= \mu_2^+(K \cap P) + \mu_2^+(K \cap N) = \mu_2^+(K). \end{aligned}$

—Joel Kindiak, 7 Jan 26, 1212H
March 30, 2026
Real-Life Hypothesis Tests
These problems arise from my actual experience, but numbers have been fudged to protect confidentiality.

Problem 1 (Population Mean). As I taught my classes, I noticed that students are exceedingly taller than I. My height is 160 cm, so I suspect that the average height $\mu$ of students is not 160 cm. By collecting the heights $x$ cm of 30 randomly chosen students, I obtained the following data:

$\Sigma x = 4840,\quad \Sigma x^2 = 781\, 176.$

Test at the 5% significance level to determine whether my suspicion is justified.
(Click for Solution)

Solution. Let $X$ denote the height of a randomly chosen student in cm, and $\mu = \mathbb E[X]$ .

We first set up the null and alternative hypotheses:

$\mathrm H_0 : \mu = 160,\quad \mathrm H_1 : \mu \neq 160.$

Denote the population variance by $\sigma^2$ and $n = 30$ . Assume $\mathrm H_0$ holds, so that $\mu = 60$ . Since $n \geq 30$ , by the central limit theorem,

$\displaystyle \frac{\bar X_n - \mu}{\sigma / \sqrt{n}} \approx Z \sim \mathcal N(0, 1).$

Since $\sigma^2$ is unknown, we need to estimate it using $s^2$ :

$\displaystyle s^2 = \frac 1{30-1} \left( 781\, 176 - \frac{4840^2}{30} \right) \approx 11.1.$

Furthermore, we estimate $\mu$ using $\bar x$ :

$\displaystyle \bar x = \frac{4840}{30} \approx 161.$

Hence, our calculated test statistic $c$ will be

$\displaystyle c := \frac{\bar x - \mu}{s/\sqrt{n}} = \frac{161.33 - 160}{\sqrt{11.126 / 30}} \approx 2.19.$

Since $n \geq 30$ , $t(n-1) \approx \mathcal N(0, 1)$ , so that using either a $z$ – or a $t$ -test would yield similar results. Denote $T \sim t(n-1)$ and the significance level $\alpha = 0.05$ .
- Using a $z$ -table, $p \leq \alpha \iff |z| \geq 1.96$ .
- Using a $t$ -table, $p \leq \alpha \iff |t| \geq 2.05$ .
Whether we let $z = c$ or $t = c$ , it is true that $p \leq \alpha$ . Therefore, there is sufficient evidence to reject $\mathrm H_0$ and conclude that Joel’s suspicion is justified, i.e. the average height of students is larger than $160$ cm.
Problem 2 (Confidence Intervals). Keep the scenario as Problem 1 but denote the true population mean by $\mu_0$ . Use the $t$ -test for simplicity. Determine the interval of values that $\mu_0$ can take such that there is insufficient evidence to reject the null hypothesis at the 5% significance.

(Click for Solution)

Solution. By definition,

$\displaystyle t = \frac{\bar x - \mu_0}{s / \sqrt n} \quad \iff \quad \mu_0 = \bar x - t \cdot \frac{s}{\sqrt n}.$

We do not reject $\mathrm H_0$ if and only if $p > \alpha = 0.05$ . Therefore,

$p > \alpha \quad \iff \quad |t| < 2.05 =: t_{\alpha/2} \quad \iff \quad -t \in (-t_{\alpha/2}, t_{\alpha/2}).$

Therefore,

$\displaystyle \mu_0 = \bar x - t \cdot \frac{s}{\sqrt n} \in \left( \bar x - t_{\alpha/2} \cdot \frac{s}{\sqrt n}, \ \bar x + t_{\alpha/2} \cdot \frac{s}{\sqrt n}\right).$

Remark 1. We call this calculated interval the $(1-\alpha)$ -confidence interval for $\mu_0$ . Denoting a specific sample $K := \{X_1,\dots, X_n\}$ , let $\bar X_K, S_K^2$ denote the corresponding computed unbiased estimators for $\mu, \sigma^2$ respectively. Then the computed corresponding confidence interval $I_K$ will equal

$I_K = \displaystyle \left( \bar X_K - t_{\alpha/2} \cdot \frac{S_K}{\sqrt n}, \bar X_K + t_{\alpha/2} \cdot \frac{S_K}{\sqrt n}\right).$

Hence, different samples would yield different confidence intervals. Since $K$ is random, so is $I_K$ . Furthermore, defining $T := (\bar X_K - \mu_0)/(S_K/\sqrt n) \sim t(n-1)$ , mimicking the computation above yields

$\mathbb P(\mu_0 \in I_K) = \mathbb P(- t_{\alpha/2} < T < t_{\alpha/2}) = 1-\alpha.$

Thus, we have the following interpretation of a $(1-\alpha)$ -confidence interval: the probability that a randomly chosen confidence interval will contain the (deterministic though unknown) population mean is $(1-\alpha)$ .

Problem 3 (Population Proportion). I went to a nearby café, and noticed that there were more women than men in the café. Out of 50 people present, 32 were women.

I suspect that it is true in general that there were more women than men in Starbucks on average. Test at the 5% significance level to determine whether my suspicion is justified.

(Click for Solution)

Solution. Let $\xi$ be a Bernoulli random variable that represents the gender of a person. Here $\xi = 0$ denotes that the person is a man and $\xi = 1$ denotes that the person is a woman. Denote $p := \mathbb E[\xi]$ , which yields the proportion of women in the café.

We first set up the null and alternative hypotheses:

$\mathrm H_0 : p = 0.5,\quad \mathrm H_1 : p > 0.5.$

Assume $\mathrm H_0$ holds, so that $p = 0.5$ . We next estimate $p$ using $\bar \xi_n$ :

$\displaystyle \bar \xi_n = \frac{32}{50} = 0.64.$

Since $n = 50 \geq 30$ and $np(1-p) = 12.5 \geq 10$ , by the central limit theorem,

$\displaystyle \frac{\bar \xi_n - p}{\sqrt{p(1-p)}/\sqrt n} \approx Z \sim \mathcal N(0, 1).$

Hence, our calculated test statistic, the $z$ -value, will be as follows:

$\displaystyle z := \frac{0.64 - 0.5}{ \sqrt{0.5 (1-0.5 )}/\sqrt{50} } \geq 1.97.$

Using a $z$ -table, $p := \mathbb P(Z > z) < 0.05 = \alpha \iff z > 1.645$ , which holds. Therefore, there is sufficient evidence to reject $\mathrm H_0$ and conclude that Joel’s suspicion is justified, i.e. there are more women than men on average.

Problem 4 (Goodness-of-Fit). A total of 750 students took an assessment worth $10$ marks. For each $k = 1, 2, \dots, 10$ , let $f(k)$ denote the number of students who scored $k$ marks out of 10. We have the following data:

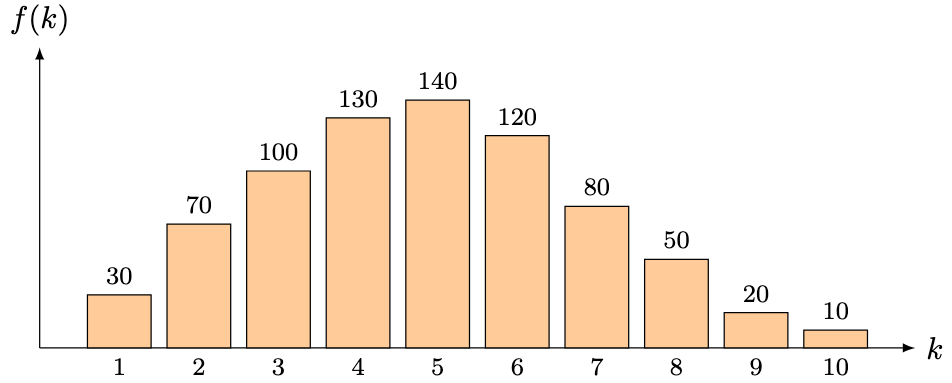
Assuming that scores are continuous, determine at the 5% significance level if the scores can be well-approximated using a normal distribution.

(Click for Solution)

Solution. Let $X$ denote the score of a randomly chosen student with $\mu = \mathbb E[X]$ and $\sigma^2 = \mathrm{Var}(X)$ . We first set up the null and alternative hypotheses:

$\mathrm H_0 : X \sim \mathcal N(\mu, \sigma^2),\quad \mathrm H_1 : X \not \sim \mathcal N(\mu, \sigma^2).$

We first estimate $\mu$ and $\sigma^2$ using $\bar x$ and $s^2$ respectively. Denoting the scores by $x$ , the summary statistics are

$\Sigma x = 3600,\quad \Sigma x^2 = 21\, 600.$

Hence,

$\displaystyle \bar x = \frac{3650}{750} \approx 4.87,\quad s^2 = \frac 1{749} \left(21\, 600 - \frac{3600^2}{750}\right) \approx 4.12.$

Now we assume $\mathrm H_0$ holds, so that $X \sim \mathcal N(4.87, 4.12)$ . Denoting

$p_k := \mathbb P(k - 0.5 < X < k + 0.5),$

we will use the test statistic

$\displaystyle W = \sum_{k=1}^{10} \frac{ (f(k) - 750p_k)^2 }{ 750p_k } \sim \chi^2(9),$

which follows a $\chi^2$ -distribution with $10-1 = 9$ degrees of freedom. For a proof for why this distribution works, refer to this document. Using relevant $z$ -table look-up values (or a spreadsheet application), we obtain the following values for $E_k \equiv 750 p_k$ (rounded to the nearest integer for readability, but whose original value we use in the final computation):

$\begin{aligned} E_1 = 25 \quad E_2 = 55 \quad E_3 &= 96 \quad E_4 = 133 \quad E_5 = 146 \\ E_6 = 125 \quad E_7 = 85 \quad E_8 &= 45 \quad E_9 = 19 \quad E_{10} = 6 \end{aligned}$

Piecing all of the values together,

$\displaystyle w = \sum_{k=1}^{10} \frac{ (f(k) - 750 p_k)^2}{ 750 p_k } \approx 1.97.$

Using a $\chi^2$ -table, $p := \mathbb P(W > w) < 0.05 = \alpha \iff w > 18.3$ , which does not hold. Therefore, there is (woefully) insufficient evidence to reject $\mathrm H_0$ and we cannot conclude that $X$ does not follow a normal distribution.

Problem 5 (Population Variance). Using the data in Problem 4, and assuming that the scores are normally distributed, test at the 5% significance level to determine if the standard deviation of assessment scores is greater than 2.

(Click for Solution)

Solution. We first set up the null and alternative hypotheses:

$\mathrm H_0 : \sigma^2 = 4, \quad \mathrm H_1 : \sigma^2 > 4.$

We use the test statistic $W := (n-1) S^2 / \sigma^2 \sim \chi(n-1)$ :

$\displaystyle w = \frac{ (750 - 1) \cdot 4.12105 }{ 4 } \approx 772.$

Using a spreadsheet application, $\mathbb P(W > w) < 0.05 = \alpha \iff w > 686$ . Therefore, there is sufficient evidence to reject $\mathrm H_0$ and conclude that $\sigma^2 > 4$ , which implies $\sigma > 2$ .

—Joel Kindiak, 4 Dec 25, 1915H
February 13, 2026
The Exponential Family
Recall that if $\lambda > 0$ and $X_n \sim \mathrm{Geom}(\lambda/n)$ , for any $x \geq 0$ ,

$\displaystyle \lim_{n \to \infty} \mathbb P\left( \frac {X_n}n > x \right) = e^{-\lambda x}.$

Definition 1. A continuous random variable is said to follow an exponential distribution with rate parameter $\lambda > 0$ , denoted $X \sim \mathrm{Exp}(\lambda)$ , if

$\mathbb P(X > x) = e^{-\lambda x}.$

Suppose $X \sim \mathrm{Exp}(\lambda)$ .

Problem 1. Prove the following properties:
- $f_X(x) = \lambda e^{-\lambda x} \cdot \mathbb I_{[0,\infty)}(x)$ ,
- $\mathbb E[X] = 1/\lambda$ ,
- $\mathrm{Var}(X) = 1/\lambda^2$ ,
- $X$ satisfies the memoryless property.
(Click for Solution)

Solution. The c.d.f. $F_X$ of $X$ for $x > 0$ is given by

$F_X(x) = \mathbb P(X \leq x) = 1 - \mathbb P(X > x) = 1 - e^{-\lambda x}.$

Hence,

$\displaystyle f_X(x) = \frac{\mathrm d}{\mathrm dx}(F_X(x)) = \frac{\mathrm d}{\mathrm dx} (1- e^{-\lambda x}) = \lambda e^{-\lambda x}.$

For the second result, we use the tail-probability characterisation of the expectation, where the interchange of integrals is valid by Fubini’s theorem:

$\begin{aligned} \mathbb E[X] &= \int_{-\infty}^{\infty} x f_X(x)\, \mathrm dx \\ &= \int_{0}^{\infty} \int_0^x f_X(x)\, \mathrm dy\, \mathrm dx \\ &= \int_{0}^{\infty} \int_{y}^\infty f_X(x) \, \mathrm dx \, \mathrm dy \\ &= \int_{0}^{\infty} \mathbb P(X > y) \, \mathrm dy. \end{aligned}$

Hence, for $X \sim \mathrm{Exp}(\lambda)$ ,

$\begin{aligned} \mathbb E[X] &= \int_{0}^{\infty} e^{-\lambda y}\, \mathrm dy = \frac 1{\lambda} \cdot [-e^{-\lambda y}]_0^\infty = \frac 1{\lambda} \cdot (0 - (-1)) = \frac 1{\lambda}. \end{aligned}$

For the variance, we adopt a similar approach:

$\begin{aligned} \mathbb E[X^2] &= \int_{-\infty}^{\infty} 2y \cdot \mathbb P(X > y) \, \mathrm dy \\ &= \int_{0}^{\infty} 2y \cdot e^{-\lambda y} \, \mathrm dy \\ &= \frac 2{\lambda} \int_0^\infty y e^{-\lambda y}\, \mathrm dy \\ &= \frac 2{\lambda} \cdot \mathbb E[X] = \frac 2{\lambda^2}. \end{aligned}$

Therefore,

$\displaystyle \mathrm{Var}(X) = \mathbb E[X^2] - \mathbb E[X]^2 = \frac{2}{\lambda^2} - \frac 1{\lambda^2} = \frac{1}{\lambda^2}.$

For the memoryless property,

$\begin{aligned} \mathbb P(X > s + t \mid X > t) &= \frac{\mathbb P(X > s + t, X > t)}{\mathbb P(X > t)} \\ &= \frac{\mathbb P(X > s+t)}{\mathbb P(X > t)} = \frac{e^{-\lambda(s+t)}}{e^{-\lambda t}} \\ &= e^{-\lambda s} = \mathbb P(X > s).\end{aligned}$

Problem 2. Suppose $Y \sim \mathrm{Exp}(\mu)$ is independent to $X$ .
- Calculate the distribution of $\min\{X, Y\}$ .
- If $\lambda = \mu$ , evaluate the p.d.f. of $X + Y$ .
(Click for Solution)

Solution. Denoting $W := \min\{X, Y\}$ ,

$\begin{aligned} \mathbb P(W > w) &= \mathbb P(X > w, Y > w) \\ &= \mathbb P(X > w) \cdot \mathbb P(Y > w)\\&= e^{-\lambda w} \cdot e^{-\mu w} \\ &= e^{-(\lambda + \mu) w}. \end{aligned}$

Hence, $\min\{X, Y\} = W \sim \mathrm{Exp}(\lambda + \mu)$ . To evaluate the p.d.f. of $U:= X+ Y$ , we compute the convolution of their individual p.d.f.s:

$\begin{aligned} f_U(u) &= (f_X * f_Y)(u) \\ &= \int_0^u f_X(x) \cdot f_Y(u-x)\, \mathrm dx \\ &= \int_0^u \lambda e^{-\lambda x} \cdot \mu e^{-\mu(u - x)}\, \mathrm dx \\ &= \lambda \cdot \mu \cdot e^{-\mu u} \cdot \int_0^u e^{-(\lambda - \mu) x} \, \mathrm dx \\ &= \lambda^2 \cdot e^{-\lambda u} \cdot \int_0^u 1 \, \mathrm dx \\ &= \lambda^2 \cdot u \cdot e^{-u}. \end{aligned}$

Definition 2. A continuous random variable $X$ is said to follow a gamma distribution with shape parameter $\alpha > 0$ and rate parameter $\lambda > 0$ , denoted $X \sim \Gamma( \alpha, \lambda)$ if it has a p.d.f. given by

$\displaystyle f_X(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)} \cdot x^{\alpha - 1} \cdot e^{-\lambda x}.$

Problem 3. Prove the following properties:
- if $X \sim \Gamma(\alpha, \lambda)$ , then $\mathbb E[X] = \alpha/\lambda$ , $\mathrm{Var}(X) = \alpha/\lambda^2$ ,
- if $X_i \sim \Gamma(\alpha_i, \lambda)$ are i.i.d., then $\sum_{i=1}^n X_i \sim \Gamma(\sum_{i=1}^n \alpha_i, \lambda)$ ,
- if $X \sim \Gamma(\alpha, \lambda)$ and $c > 0$ , then $cX \sim \Gamma(\alpha, \lambda/c)$ .
(Click for Solution)

Solution. Suppose $Y \sim \Gamma(\alpha + 1,\lambda)$ . By definition of the expectation,

$\begin{aligned} \mathbb E[X^n] &= \int_0^\infty x^n \cdot \frac{\lambda^\alpha}{\Gamma(\alpha)} \cdot x^{\alpha - 1} \cdot e^{-\lambda x}\, \mathrm dx \\ &= \frac {\alpha \cdot (\alpha+1) \cdot \cdots \cdot (\alpha +n-1)}{\lambda^n} \cdot \int_0^\infty \frac{\lambda^{\alpha+n}}{\Gamma(\alpha+1)} \cdot x^{(\alpha + n) - 1} \cdot e^{-\lambda x}\, \mathrm dx \\ &= \frac{\alpha \cdot (\alpha+1) \cdot \cdots \cdot (\alpha +n-1)}{\lambda^n} \cdot \int_0^\infty f_Y(x)\, \mathrm dx \\ &= \frac{\alpha \cdot (\alpha+1) \cdot \cdots \cdot (\alpha +n-1)}{\lambda^n} . \end{aligned}$

Hence, $\mathbb E[X] = \alpha/\lambda$ , and

$\begin{aligned} \mathrm{Var}(X) &= \mathbb E[X^2] - \mathbb E[X]^2 = \frac{\alpha \cdot (\alpha+1)}{\lambda^2} - \frac{\alpha^2}{\lambda^2} = \frac{\alpha}{\lambda^2}. \end{aligned}$

We prove the second result by induction. Suppose $X \sim \Gamma(\alpha, \lambda)$ and $Y \sim \Gamma (\beta, \lambda)$ are independent. To evaluate the p.d.f. of $U:= X+ Y$ , we compute the convolution of their individual p.d.f.s:

$\begin{aligned} f_U(u) &= (f_X * f_Y)(u) \\ &= \int_0^u f_X(x) \cdot f_Y(u-x)\, \mathrm dx \\ &= \int_0^u \frac{\lambda^\alpha}{\Gamma(\alpha)} \cdot x^{\alpha - 1} \cdot e^{-\lambda x} \cdot \frac{\lambda^\beta}{\Gamma(\beta)} \cdot (u-x)^{\beta - 1} \cdot e^{-\lambda (u-x)}\, \mathrm dx \\ &= \frac{\lambda^{\alpha + \beta}}{\Gamma(\alpha) \cdot \Gamma(\beta)} \cdot \int_0^u x^{\alpha - 1} \cdot (u-x)^{\beta - 1} \cdot e^{-\lambda u}\, \mathrm dx \\ &= \frac{\lambda^{\alpha + \beta}}{\Gamma(\alpha) \cdot \Gamma(\beta)} \cdot \int_0^1 (ut)^{\alpha - 1} \cdot (u-ut)^{\beta - 1} \cdot e^{-\lambda u}\cdot u\, \mathrm dt \\ &= \frac{\lambda^{\alpha + \beta}}{\Gamma(\alpha + \beta)} \cdot u^{(\alpha+\beta) -1}\cdot e^{-\lambda u} \cdot \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \cdot \Gamma(\beta)} \cdot \int_0^1 t^{\alpha - 1} \cdot (1-t)^{\beta - 1} \, \mathrm dt \\ &= \frac{\lambda^{\alpha + \beta}}{\Gamma(\alpha + \beta)} \cdot u^{(\alpha+\beta) -1}\cdot e^{-\lambda u}. \end{aligned}$

Therefore, $W \sim \Gamma(\alpha +\beta, \lambda)$ . Inductively, if $X_i \sim \Gamma(\alpha_i, \lambda)$ are i.i.d.,

$\displaystyle \sum_{i=1}^{k+1} X_i = \sum_{i=1}^{k} X_i + X_{k+1} \sim \Gamma \left( \sum_{i=1}^{k} \alpha_i + \alpha_{k+1}, \lambda \right) = \Gamma \left( \sum_{i=1}^{k+1} \alpha_i, \lambda \right).$

For the final property, denoting $V := cX$ ,

$\begin{aligned} f_{V}(v) = f_{cX}(v) &= \frac 1c \cdot f_X\left( \frac vc \right) \\ &= \frac 1c \cdot \frac{\lambda^\alpha}{\Gamma(\alpha)} \cdot \left( \frac vc \right)^{\alpha - 1} \cdot e^{-\lambda v/c} \\ &= \frac{(\lambda /c)^\alpha}{\Gamma(\alpha)} \cdot v^{\alpha - 1} \cdot e^{-(\lambda /c) v}. \end{aligned}$

Hence, $cX = V \sim \Gamma(\alpha, \lambda / c)$ .

Given probability distributions $\mathbb Q_1, \mathbb Q_2$ , write $\mathbb Q_1 =\mathbb Q_2$ if there exists a random variable $X$ such that $X \sim \mathbb Q_1$ and $X \sim \mathbb Q_2$ .

Problem 4. Prove the following properties:
- $\mathrm{Exp}(\lambda) = \Gamma(1, \lambda)$ ,
- $\Gamma(\nu/2, 1/2) = \chi^2(\nu)$ ,
- for i.i.d. $X_1,\dots, X_n \sim \mathrm{Exp}(\lambda)$ , $\sum_{i=1}^n X_i \sim \Gamma(n, \lambda),\bar X \sim \Gamma(n, \lambda/n)$ ,
- for any fixed $c > 0$ , if $W \sim \chi^2(\nu)$ , then $cW \sim \Gamma(\nu/2, 1/(2c))$ .
(Click for Solution)

Solution. We note that if $X \sim \Gamma( 1,\lambda)$ , since $\Gamma(1) = 0! = 1$ ,

$\displaystyle f_X(x) = \frac{\lambda}{\Gamma(1)} \cdot x^{1 - 1} \cdot e^{-\lambda x} = \lambda e^{-\lambda x},$

so that $X \sim \mathrm{Exp}(1, \lambda)$ . If $X \sim \Gamma( \nu/2, 1/2)$ , then

$\displaystyle f_X(x) = \frac{(1/2)^{\nu/2}}{\Gamma(\nu/2)} \cdot x^{\nu/2 - 1} \cdot e^{-x/2} = \frac{1}{2^{\nu/2} \cdot \Gamma(\nu/2)} \cdot x^{\nu/2 - 1} \cdot e^{-x/2}.$

The last two results are immediate corollaries of Problem 3.

These probability distributions are examples of the exponential family of probability distributions.

—Joel Kindiak, 4 Aug 25, 1356H
January 9, 2026
The Geometric Distribution

Definition 1. For $K \subseteq \mathbb R$ , a random variable $X : \Omega \to K$ satisfies the memoryless property if the following holds: for any $s, t \in K$ ,

$\displaystyle \mathbb P(X > s + t \mid X > t) = \mathbb P(X > s).$

Problem 1. If $K = \mathbb N^+$ and $X$ satisfies the memoryless property, compute an expression for $\mathbb P(X = x)$ in terms of $p := \mathbb P(X = 1)$ .

(Click for Solution)

Solution. Define the function $G$ by $G(x):= \mathbb P(X > x)$ . By the definition of conditional probability,

$\begin{aligned} G(s+t) = \mathbb P(X > s+t) &= \mathbb P(X > s +t, X>t) \\ &= \mathbb P(X > s +t \mid X>t) \cdot \mathbb P(X > t) \\ &= \mathbb P(X > s) \cdot \mathbb P(X > t) \\ &= G(s) \cdot G(t). \end{aligned}$

Therefore, $G(x) = a^x$ for some $a > 0$ . In particular,

$a = G(1) = \mathbb P(X > 1) = 1 - \mathbb P(X=1) = 1-p.$

Therefore, $G(x) = (1-p)^x$ , so that

$\begin{aligned} \mathbb P(X=x) &= \mathbb P(X > x-1) - \mathbb P(X > x) \\ &= (1-p)^{x-1} - (1-p)^x \\ &= (1-p)^{x-1} \cdot (1 - (1-p)) \\ &= (1-p)^{x-1} \cdot p. \end{aligned}$

Definition 2. A discrete random variable $X : \Omega \to \mathbb N^+$ is said to follow a geometric distribution with success probability $p$ , denoted $X \sim \mathrm{Geom}(p)$ , if

$\displaystyle \mathbb P(X = x) = (1-p)^{x-1} \cdot p,\quad x \in \mathbb N^+.$

Suppose $X \sim \mathrm{Geom}(p)$ .

Problem 2. Prove that $X$ satisfies the memoryless property.

(Click for Solution)

Solution. Using a geometric series,

$\begin{aligned} \mathbb P(X > x) &= \sum_{k=x+1}^\infty \mathbb P(X = k) \\ &= \sum_{k=x+1}^\infty (1-p)^{k-1} \cdot p \\ &= \frac{p\cdot (1-p)^x}{1 - (1-p)} = (1-p)^x. \end{aligned}$

By the definition of conditional probability,

$\begin{aligned} \mathbb P(X > s +t \mid X>t) &= \frac{\mathbb P(X > s +t, X>t)}{\mathbb P(X > t)} \\ &= \frac{\mathbb P(X > s +t)}{\mathbb P(X > t)} \\ &= \frac{(1-p)^{s+t}}{(1-p)^t} \\ &= (1-p)^s = \mathbb P(X > s). \end{aligned}$

Problem 3. Prove that $\displaystyle \mathbb E[X] = \sum_{x = 0}^\infty \mathbb P(X > x)$ . Hence, evaluate $\mathbb E[X]$ and $\mathrm{Var}(X)$ .

(Click for Solution)

Solution. By interchanging sums,

$\begin{aligned} \mathbb E[X] &= \sum_{x = 0}^\infty x \cdot \mathbb P(X = x) = \sum_{x=0}^\infty \sum_{y=0}^{x-1} \mathbb P(X = x) \\ &= \sum_{y=0}^\infty \sum_{x=y+1}^\infty \mathbb P(X = x) = \sum_{y=0}^\infty \mathbb P(X > y) = \sum_{x = 0}^\infty \mathbb P(X > x). \end{aligned}$

Hence, using the calculations in Problem 2,

$\displaystyle \mathbb E[X] = \sum_{x=0}^\infty (1-p)^x = \frac{1}{1-(1-p)} = \frac 1p.$

For the variance, we first compute $\mathbb E[X^2]$ . Observe that

$\displaystyle \sum_{y=0}^{x-1} (2y + 1) = x^2.$

Therefore, by interchanging sums,

$\begin{aligned} \mathbb E[X^2] &= \sum_{x = 0}^\infty x^2 \cdot \mathbb P(X = x) \\ &= \sum_{x=0}^\infty \sum_{y=0}^{x-1} (2y + 1) \cdot \mathbb P(X = x) \\ &= \sum_{y=0}^\infty \sum_{x=y+1}^\infty (2y + 1) \cdot \mathbb P(X = x) \\ &= \sum_{y=0}^\infty \left( (2y + 1) \cdot \sum_{x=y+1}^\infty (1-p)^{x-1} \cdot p \right) \\ &= \sum_{y=0}^\infty \left( (2y + 1) \cdot \frac{(1-p)^y}{1 - (1-p)} \cdot p \right) \\ &= \frac 1p \cdot \sum_{y=0}^\infty \left( (2y + 1) \cdot (1-p)^y \cdot p \right) \\ &= \frac 1p \cdot \left( p + (1-p) \cdot \left( 2 \cdot \sum_{y=1}^\infty y\cdot \mathbb P(X = y ) + \sum_{y=1}^\infty \mathbb P(X = y ) \right) \right) \\ &= \frac 1p \cdot \left( p + (1-p) \cdot \left( \frac 2p + 1 \right) \right) \\ &= 1 + \left( \frac 1p - 1 \right) \cdot \left( \frac 2p + 1 \right) \\ &= 1 + \frac 2{p^2} + \frac 1p - \frac 2p - 1 = \frac {2-p}{p^2}. \end{aligned}$

Therefore,

$\begin{aligned} \mathrm{Var}(X) &= \mathbb E[X^2] -\mathbb E[X]^2 = \frac {2-p}{p^2} - \frac 1{p^2} = \frac{1-p}{p^2}. \end{aligned}$

Problem 4. If $Y \sim \mathrm{Geom}(q)$ is independent of $X$ , compute the distribution of $\min\{X, Y\}$ .

(Click for Solution)

Solution. Denote $W := \min \{X, Y\}$ . Then

$\begin{aligned} \mathbb P(W > w) &= \mathbb P(\min\{X,Y\} > w) \\ &= \mathbb P(X > w, Y > w) \\ &= \mathbb P(X > w) \cdot \mathbb P(Y > w) \\ &= (1-p)^w \cdot (1-q)^w = ((1-p)(1-q))^w. \end{aligned}$

Therefore, $\min\{X, Y\} \sim \mathrm{Geom}(1-(1-p)(1-q))$ .

Problem 5. Fix $\lambda > 0$ . Suppose $X_n \sim \mathrm{Geom}(\lambda /n)$ . For any $x > 0$ , evaluate

$\displaystyle \lim_{n \to \infty} \mathbb P \left( \frac {X_n}n > x \right) .$

(Click for Solution)

Solution. Using the tail-probability,

$\begin{aligned} \lim_{n \to \infty} \mathbb P \left( \frac {X_n}n > x \right) &= \lim_{n \to \infty} \mathbb P(X_n > nx) \\ &= \lim_{n \to \infty} \left( 1 - \frac{\lambda}n \right)^{nx} \\ &= \left( \lim_{n \to \infty} \left( 1 - \frac{\lambda}n \right)^{n} \right)^x \\ &= (e^{-\lambda})^x = e^{-\lambda x}. \end{aligned}$

—Joel Kindiak, 3 Aug 25, 0004H

January 6, 2026
The Gaussian Integral

Problem 1. Evaluate the Gaussian integral $\displaystyle \int_{-\infty}^{\infty} e^{-x^2}\, \mathrm dx$ .

(Click for Solution)

Solution. Since $e^{-x^2}$ is even in $x$ ,

$\displaystyle \int_{-\infty}^{\infty} e^{-x^2}\, \mathrm dx = 2 \cdot \int_{0}^{\infty} e^{-x^2}\, \mathrm dx.$

For the right-hand side,

$\begin{aligned}\left( \int_{0}^{\infty} e^{-x^2}\, \mathrm dx \right)^2 &= \left( \int_{0}^{\infty} e^{-x^2}\, \mathrm dx \right) \cdot \left( \int_{0}^{\infty} e^{-y^2}\, \mathrm dy \right) \\ &= \int_0^\infty e^{-x^2} \cdot \left( \int_0^\infty e^{-y^2}\, \mathrm dy \right)\, \mathrm dx \\ &= \int_0^\infty e^{-x^2} \cdot \left( \int_0^\infty e^{-u^2x^2} \cdot x\, \mathrm du \right)\, \mathrm dx \\ &= \int_0^\infty \int_0^\infty xe^{-x^2(u^2+1)} \, \mathrm du\, \mathrm dx. \end{aligned}$

By Fubini’s theorem,

$\begin{aligned}\left( \int_{0}^{\infty} e^{-x^2}\, \mathrm dx \right)^2 &= \int_0^\infty \int_0^\infty xe^{-x^2(u^2+1)} \, \mathrm du\, \mathrm dx\\ &= \int_0^\infty \int_0^\infty xe^{-x^2(u^2+1)} \, \mathrm dx\, \mathrm du \\ &= \int_0^\infty \left[ -\frac 1{2(u^2+1)} \cdot e^{-x^2(u^2+1)} \right]_0^\infty\, \mathrm du \\ &= \int_0^\infty \frac 1{2(u^2+1)}\, \mathrm du \\ &= \frac 12 \cdot [\tan^{-1}(u)]_0^{\infty} \\ &= \frac 12 \cdot \frac{\pi}2 = \frac{\pi}{4}. \end{aligned}$

Taking square roots,

$\displaystyle \int_{0}^{\infty} e^{-x^2}\, \mathrm dx = \frac{\sqrt{\pi}}{2} \quad \Rightarrow \quad \int_{-\infty}^{\infty} e^{-x^2}\, \mathrm dx = \sqrt{\pi}.$

This calculation was authored by Hirokazu Iwasawa.

—Joel Kindiak, 26 Jul 25, 2156H

January 2, 2026
The Poisson Distribution

Definition 1. The random variable $X : \Omega \to \mathbb N_0$ follows a Poisson distribution with rate parameter $\lambda > 0$ , denoted $X \sim \mathrm{Pois}(\lambda)$ , if

$\displaystyle \mathbb P(X=x) = c_\lambda \cdot \frac{\lambda^x}{x!}$

for some $c_\lambda > 0$ .

Problem 1. Evaluate $c_\lambda$ .

(Click for Solution)

Solution. We require $\sum_{x = 0}^\infty \mathbb P(X=x) = 1$ :

$\begin{aligned}1 = \sum_{x = 0}^\infty \mathbb P(X=x) &= \sum_{x =0}^\infty c_\lambda \cdot \frac{\lambda^x}{x!} = c_\lambda \cdot \sum_{x = 0}^\infty \frac{\lambda^x}{x!} = c_\lambda \cdot e^{\lambda}. \end{aligned}$

Therefore, $c_\lambda = e^{-\lambda}$ .

Problem 2. Evaluate $\mathbb E[X]$ and $\mathrm{Var}(X)$ .

(Click for Solution)

Solution. By definition of the expectation,

$\begin{aligned} \mathbb E[X] &= \sum_{x = 0}^\infty x \cdot \mathbb P(X=x) \\ &= \sum_{x = 1}^\infty x \cdot c_\lambda \cdot \frac{\lambda^x}{x!} \\ &= \lambda \cdot \sum_{x = 1}^\infty c_\lambda \cdot \frac{\lambda^{x-1}}{(x-1)!} \\ &= \lambda \cdot \sum_{x = 0}^\infty c_\lambda \cdot \frac{\lambda^{x}}{x!} = \lambda \cdot 1 = \lambda. \end{aligned}$

For the variance, we compute the term

$\begin{aligned}\mathbb E[X(X-1)] &= \sum_{x = 0}^\infty x(x-1) \cdot \mathbb P(X=x) \\ &= \sum_{x = 2}^\infty x(x-1) \cdot c_\lambda \cdot \frac{\lambda^x}{x!} \\ &= \lambda^2 \cdot \sum_{x = 2}^\infty c_\lambda \cdot \frac{\lambda^{x-2}}{(x-2)!} \\ &= \lambda^2 \cdot 1 = \lambda^2. \end{aligned}$

Therefore,

$\begin{aligned} \mathrm{Var}(X) &= \mathbb E[X^2] - \mathbb E[X]^2 \\ &= \mathbb E[X(X-1)] + \mathbb E[X] - \mathbb E[X]^2 \\ &= \lambda^2 + \lambda - \lambda^2 = \lambda.\end{aligned}$

Problem 3. Given that $X \sim \mathrm{Pois}(\lambda)$ and $Y \sim \mathrm{Pois}(\mu)$ are independent, determine the distribution of $X + Y$ .

(Click for Solution)

Solution. Denoting $W := X+Y$ , we take the discrete convolution of the p.d.f.s of $X,Y$ to obtain

$\begin{aligned}f_W (w) &= \sum_{x = 0}^w f_X(x) \cdot f_Y(w-x) \\ &= \sum_{x=0}^w c_\lambda \cdot \frac{\lambda^x}{x!} \cdot c_\mu \cdot \frac{\lambda^{w-x}}{(w-x)!} \\ &= \sum_{x=0}^w c_\lambda \cdot \frac{\lambda^x}{x!} \cdot c_\mu \cdot \frac{\mu^{w-x}}{(w-x)!} \\ &= c_\lambda \cdot c_\mu \cdot \sum_{x=0}^w \frac{\lambda^x}{x!} \cdot \frac{\mu^{w-x}}{(w-x)!} \\ &= c_\lambda \cdot c_\mu \cdot \frac 1{w!} \cdot \sum_{x=0}^w \frac{w!}{x! \cdot (w-x)!} \cdot \lambda^x \cdot \mu^{w-x} \\ &= c_\lambda \cdot c_\mu \cdot \frac 1{w!} \cdot \sum_{x=0}^w {w \choose x} \cdot \lambda^x \cdot \mu^{w-x} \\ &= c_\lambda \cdot c_\mu \cdot \frac {(\lambda + \mu)^w}{w!}.\end{aligned}$

Furthermore, $c_\lambda \cdot c_\mu = e^{-\lambda} \cdot e^{\mu} = e^{-(\lambda + \mu)} = c_{\lambda + \mu}$ . Hence,

$\displaystyle \mathbb P(X+Y = w) = c_{\lambda + \mu} \cdot \frac{(\lambda + \mu)^w}{w!},$

so that $X +Y \sim \mathrm{Pois}(\lambda + \mu)$ .

Problem 4. Fix $\lambda > 0$ . Suppose $X_n \sim \mathrm{Bin}(n, \lambda/n)$ and $Y \sim \mathrm{Pois}(\lambda)$ . Prove that $f_{X_n} \to f_Y$ .

(Click for Solution)

Solution. Fix $y \in \mathbb N_0$ . For each $n$ ,

$\begin{aligned} f_{X_n}(y) &= {n \choose y} \left(1 - \frac{\lambda}{n}\right)^{n-y} \left( \frac{\lambda}n \right)^y \\ &= \frac{n(n-1) \cdot \dots \cdot (n-y+1)}{y!} \cdot \frac{\lambda^y }{n^y } \cdot \left(1 - \frac{\lambda}{n}\right)^{n-y} \\ &= \frac{n}{n} \cdot \frac{n-1}{n} \cdot \cdots \cdot \frac{n-y+1}n \cdot \left(1 - \frac{\lambda}{n}\right)^{-y} \cdot \left(1 - \frac{\lambda}{n}\right)^{n} \cdot \frac{\lambda^y }{y! } \end{aligned}$

Taking $n \to \infty$ ,

$\displaystyle \lim_{n \to \infty} f_{X_n}(y) = 1 \cdot 1 \cdot e^{-\lambda} \cdot \frac{\lambda^y}{y!} = e^{-\lambda} \cdot \frac{\lambda^y}{y!} = f_Y(y).$

—Joel Kindiak, 1 Aug 25, 1751H

December 30, 2025
Proving Feynman’s Trick
Feynman’s trick in differentiating under the integral sign has been creatively wielded to evaluate otherwise intractable integrals. In this exercise, we prove Feynman’s trick and use it to evaluate the seemingly intractable Dirichlet integral

$\displaystyle \int_{-\infty}^{\infty} \frac{\sin x}{x}\, \mathrm dx.$

Let $(\Omega, \mathcal F, \mathbb R)$ be a measure space and $f : \Omega \times [a, b] \to \mathbb R$ be a function such that for each $t \in [a, b]$ , $f( \cdot, t)$ is measurable.

Problem 1. Suppose the following conditions:
- For any $\omega \in \Omega$ , $f(\omega, \cdot)$ is continuous.
- There exists some non-negative integrable $g : \Omega \to \mathbb R$ such that for any $(\omega, t) \in \Omega \times [a, b]$ , $|f( \omega ,t)| \leq g(\omega)$ .
Prove that the map $F : [a, b] \to \mathbb R$ defined by $\displaystyle F(t) : = \int_{\Omega} f(\cdot , t)\, \mathrm d\mu$ is continuous.

(Click for Solution)

Solution. Fix $t_n \to t$ . For any $\omega \in \Omega$ , since $f(\omega, \cdot)$ is continuous,

$f(\omega, t_n) \to f(\omega, t),$

so that $f(\cdot, t_n) \to f(\cdot, t)$ pointwise. Furthermore,

$\displaystyle \int_{\Omega} |f(\cdot, t)|\, \mathrm d\mu \leq \int_{\Omega} g\, \mathrm d\mu < \infty,$

so that $f(\cdot, t_n)$ and $f(\cdot, t)$ are all integrable.

Since $g$ is integrable, by Lebesgue’s dominated convergence theorem,

$\displaystyle F(t_n) = \lim_{n \to \infty} \int_{\Omega} f(\cdot , t_n)\, \mathrm d\mu= \int_{\Omega} f(\cdot , t)\, \mathrm d\mu = F(t),$

so that $F$ is continuous, as required.

Problem 2. Suppose the following conditions:
- There exists some $t_0 \in [a, b]$ such that $f(\cdot, t_0)$ is integrable.
- For each $\omega \in \Omega$ , $f(\omega, \cdot)$ is differentiable with derivative at $t_0$ denoted by $\frac{\partial f}{\partial t}(\omega,t_0)$ .
- There exists some non-negative integrable $g : \Omega \to \mathbb R$ such that for any $(\omega, t) \in \Omega \times [a, b]$ , $\left|\frac{\partial f}{\partial t} (\omega,t) \right| \leq g( \omega )$ .
Prove that the map $F : [a, b] \to \mathbb R$ defined by $\displaystyle F(t) : = \int_{\Omega} f(\cdot, t)\, \mathrm d\mu$ is differentiable on $[a, b]$ and

$\displaystyle F'(t) = \frac{\mathrm d}{\mathrm dt} \int_{\Omega} f(\omega, t)\, \mathrm d\mu(\omega) = \int_{\Omega} \frac{\partial f}{\partial t}(\omega, t)\, \mathrm d\mu(\omega).$

(Click for Solution)

Solution. We first check that $F$ is well-defined. By hypothesis, $F(t_0)$ is well-defined. Fix $t \in [a, b]$ . By the mean value theorem, there exists $c$ between $t_0$ and latex t$ such that

$\displaystyle \frac{ |f(\omega, t) - f(\omega, t_0)| }{ |t - t_0| } = \left| \frac{ \partial f }{ \partial t} (\omega, c) \right| \leq g(\omega).$

By performing more analysis, $f(\cdot, t)$ is integrable, so that $F(t)$ is well-defined.

Now fix $\omega \in \Omega$ . For any $t_n \to t$ , since each $f(\cdot, t_n) - f(\cdot, t)$ is measurable,

$\displaystyle \frac{\partial f}{\partial t}(\omega, t) := \lim_{n \to \infty} \underbrace{ \frac{f(\omega, t_n) - f(\omega, t)}{ t_n - t} }_{\varphi_n(\omega)}$

is measurable. Furthermore, $\varphi_n \to \frac{\partial f}{\partial t} (\cdot, t)$ pointwise. We claim that $|\varphi_n| \leq g$ , since the mean value theorem gives $c$ between $t_n$ and $t$ such that

$\displaystyle \frac{ | f(\omega, t_n) - f(\omega, t) |}{ | t_n - t | } = \left| \frac{\partial f}{\partial t}(\omega, c) \right| \leq g(\omega).$

By algebruh and the triangle inequality, each $\varphi_n$ is integrable. Hence, by Lebesgue’s dominated convergence theorem,

$\begin{aligned} \lim_{t_n \to t} \int_{\Omega} \frac{f(\omega, t_n) - f(\omega, t)}{t_n - t}\, \mathrm d\mu(\omega) &= \lim_{n \to \infty} \int_{\Omega} \varphi_n\, \mathrm d\mu \\ &= \int_{\Omega} \lim_{n \to \infty} \varphi_n\, \mathrm d\mu = \int_{\Omega} \frac{\partial f}{\partial t} (\cdot, t)\, \mathrm d\mu. \end{aligned}$

On the other hand, by bookkeeping

$\begin{aligned} \frac{ \mathrm d }{ \mathrm dt } F(t) &= \lim_{ t_n \to t } \frac{ F(t_n) - F(t) }{ t_n - t } \\ &= \lim_{t_n \to t} \int_{\Omega} \frac{f(\omega, t_n) - f(\omega, t)}{t_n - t}\, \mathrm d\mu(\omega) \\ &= \int_{\Omega} \frac{\partial f}{\partial t} (\omega, t)\, \mathrm d\mu(\omega). \end{aligned}$

Therefore,

$\displaystyle F'(t) = \frac{\mathrm d}{\mathrm dt} \int f(\omega, t)\, \mathrm d\mu(\omega) = \int \frac{\partial f}{\partial t}(\omega, t)\, \mathrm d\mu(\omega).$

Remark 1. Thanks to Problem 2, our proof that $\mathcal L\{tf'(t)\} = -\mathcal L\{f\}'(s)$ in the study of differential equations becomes a logically correct one.

Problem 3. Use Problem 2 to evaluate $\displaystyle \int_{-\infty}^{\infty} \frac{\sin x}{x}\, \mathrm dx$ .

(Click for Solution)

Solution. Define the function $I$ by

$\displaystyle I(y) := \int_{0}^{\infty} \frac{\sin x}{x} \cdot e^{-xy}\, \mathrm dy$

that satisfies the hypotheses of Problem 2, and our goal is to evaluate $2 \cdot I(0)$ . Applying Problem 2 and integrating by parts,

$\begin{aligned} I'(y) &= \int_{0}^{\infty} \frac{\partial}{\partial y} \left( \frac{\sin x}{x} \cdot e^{-xy} \right) \, \mathrm dx \\ &= \int_{0}^{\infty} \frac{\sin x}{x} \cdot -xe^{-xy} \, \mathrm dx \\ &= -\int_{0}^{\infty} e^{-xy} \cdot \sin x \, \mathrm dx \\ &= -\left[ \frac{e^{-xy}}{(-y)^2 + 1^2} \cdot ((-y) \sin(x) - \cos(x)) \right]_{0}^{\infty} \\ &= -\frac{1}{1+y^2}. \end{aligned}$

Integrating and applying the first fundamental theorem of calculus,

$\displaystyle I(y) = I(0) - \int_0^y \frac{1}{1+y^2}\, \mathrm dy = I(0) - \tan^{-1}(y).$

Since $I$ is continuous,

$\displaystyle \lim_{y \to \infty} I(y) = \int_0^\infty \lim_{y \to \infty} \frac{\sin x}{x} \cdot e^{-xy}\, \mathrm dx = \int_0^\infty 0\, \mathrm dx = 0.$

Taking $y \to \infty$ on all sides, therefore,

$\displaystyle 0 = I(0) - \frac{\pi}{2} \quad \Rightarrow \quad I(0) = \frac{\pi}{2}.$

Therefore, the Dirichlet integral evaluates to

$\displaystyle \int_{-\infty}^{\infty} \frac{\sin x}{x}\, \mathrm dx = 2 \cdot I(0) = \pi.$

—Joel Kindiak, 29 Jul 25, 1319H
December 26, 2025
Binomial Theorem Corollaries

Recall the binomial theorem, which states that for any $n \in \mathbb N$ and $x \in \mathbb R$ ,

$\displaystyle (1 + x)^n = \sum_{k=0}^n {n \choose k} x^k,$

where we define $0^0 := 1$ by convention.

Problem 1. Prove that for any $a, b \in \mathbb R$ ,

$\displaystyle (a + b)^n = \sum_{k=0}^n {n \choose k} a^{n-k} b^k.$

(Click for Solution)

Solution. If $a = 0$ then the result is trivial. If $a > 0$ , then

$\begin{aligned} (a+b)^n &= a^n \cdot \left(1 + \frac ba\right)^n = a^n \cdot \sum_{k=0}^n \left( \frac ba \right)^k \\ &= a^n \cdot \sum_{k=0}^n a^{-k} \cdot b^k = \sum_{k=0}^n a^{n-k} \cdot b^k. \end{aligned}$

Problem 2. Evaluate the sums $\displaystyle \sum_{k=0}^n {n \choose k}$ and $\displaystyle \sum_{k=0}^n (-1)^k {n \choose k}$ .

(Click for Solution)

Solution. By Problem 1,

$\displaystyle (1 + (\pm 1))^n = \sum_{k=0}^n (\pm 1)^k {n \choose k}.$

Therefore, $\displaystyle \sum_{k=0}^n {n \choose k} = (1+1)^n = 2^n$ and $\displaystyle \sum_{k=0}^n (-1)^k {n \choose k} = (1-1)^n = 0$ .

Problem 3. Prove that $\displaystyle \sum_{k \in \mathbb N_0 :\, 2k \leq n} {n \choose 2k} = \sum_{k \in \mathbb N_0 :\, 2k+1 \leq n} {n \choose 2k+1}$ .

(Click for Solution)

Solution. By Problem 2,

$\begin{aligned} 0=\sum_{k=0}^n (-1)^k {n \choose k} &= \sum_{k \in \mathbb N_0 :\, 2k \leq n} (-1)^{2k} {n \choose 2k} + \sum_{k \in \mathbb N_0 :\, 2k+1 \leq n} (-1)^{2k+1} {n \choose 2k+1} \\ &= \sum_{k \in \mathbb N_0 :\, 2k \leq n} {n \choose 2k} - \sum_{k \in \mathbb N_0 :\, 2k+1 \leq n} {n \choose 2k+1}. \end{aligned}$

Therefore,

$\displaystyle \sum_{k \in \mathbb N_0 :\, 2k \leq n} {n \choose 2k} = \sum_{k \in \mathbb N_0 :\, 2k+1 \leq n} {n \choose 2k+1}.$

Problem 4. Evaluate the sums $\displaystyle \sum_{k= 1}^n k {n \choose k}$ and $\displaystyle \sum_{k= 1}^n k^2 {n \choose k}$ .

(Click for Solution)

Solution. Recall the vanilla binomial theorem

$\displaystyle (1 + x)^n = \sum_{k=0}^n {n \choose k} x^k.$

Differentiating on both sides twice,

$\begin{aligned} n(1+x)^{n-1} &= \sum_{k=1}^{n} k {n \choose k} x^{k-1}, \\ n(n-1)(1+x)^{n-2} &= \sum_{k=2}^{n} k(k-1) {n \choose k} x^{k-2}. \end{aligned}$

Setting $x = 1$ in the first identity,

$\displaystyle \sum_{k=1}^{n} k {n \choose k} = n \cdot 2^{n-1}.$

Setting $x = 1$ in the second identity,

$\begin{aligned} n(n-1)\cdot 2^{n-2} &= \sum_{k=2}^{n} k(k-1) {n \choose k} = \sum_{k=2}^{n} k^2 {n \choose k} - \sum_{k=2}^{n} k {n \choose k}. \end{aligned}$

By algebruh, since $\displaystyle 1^r {n \choose 1} = n$ for any $r$ ,

$\displaystyle \sum_{k=1}^{n} k^2 {n \choose k} = n(n-1)\cdot 2^{n-2} + n \cdot 2^{n-1} = n \cdot 2^{n-1} \cdot (2n-1).$

Problem 5. Evaluate $\displaystyle \sum_{k= 0}^r {m \choose k} {n \choose r-k}$ .

(Click for Solution)

Solution. Using the binomial theorem on the product

$\displaystyle (1+x)^{m+n} = (1+x)^m (1+x)^n,$

we have

$\begin{aligned} \sum_{r=0}^{m+n} {m+n \choose r} x^r &= \left(\sum_{k=0}^m {m \choose k} x^k\right) \cdot \left(\sum_{l=0}^n {n \choose l} x^l\right) \\ &= \sum_{k=0}^m \sum_{l=0}^n {m \choose k} {n \choose l} x^{k+l} \\ &= \sum_{r=0}^{m+n} \sum_{k+l=r} {m \choose k} {n \choose l} x^r \\ &= \sum_{r=0}^{m+n} \sum_{k=0}^r {m \choose k} {n \choose r-k} x^r. \end{aligned}$

Comparing the coefficients of $x^r$ ,

$\displaystyle \sum_{k= 0}^r {m \choose k} {n \choose r-k} = {m+n \choose r}.$

This result is known as Vandermonde’s identity.

Problem 6. Evaluate $\displaystyle \sum_{k= 0}^n {n \choose k}^2$ .

(Click for Solution)

Solution. Setting $m = n$ and $r = 2k$ in Problem 5,

$\displaystyle \sum_{k= 0}^n {n \choose k}^2 = \sum_{k= 0}^r {n \choose k} {n \choose 2k-k} = {n + n \choose k} = {2n \choose k}.$

—Joel Kindiak, 1 Aug 25, 1520H

December 23, 2025
Several Probability Puzzles

Problem 1. Let $X_1,\dots, X_n \sim \mathcal U(0, 1)$ be i.i.d.. Let $g : [0,1]^n \to [0,1]^n$ denote the permutation

$g(x_1,\dots, x_n) = (y_1,\dots, y_n)$

such that $y_1 \leq \dots \leq y_n$ . Denoting $(Y_1,\dots, Y_n) = g(X_1, \dots, X_n)$ , evaluate $\mathbb E[Y_i]$ for each $i$ .

(Click for Solution)

Solution. Since $\mathbb P (X_i = X_j) = 0$ whenever $i \neq j$ , we can assume $Y_1 < \dots < Y_n$ .

We will obtain the distribution of $Y_i$ . Fix $x \in [0, 1]$ . Let $V_x \sim \mathrm{Bin}(n-1, x)$ denote the number of sample points that are less than $x$ , which follows a binomial distribution. It follows that $\{ Y_i = x \} = \{ V_x = i-1 \}$ , so that

$\displaystyle f_{Y_i} (x) = \mathbb P(V_x = i-1) = {n-1 \choose i-1} x^{i-1} (1-x)^{n-i}.$

Hence, by recalling the properties of the Beta distribution,

$\begin{aligned} \mathbb E[Y_i] &= \int_0^1 x \cdot f_{Y_i} (x)\, \mathrm dx \\ &= \int_0^1 x \cdot {n-1 \choose i-1} x^{i-1} (1-x)^{n-i}\, \mathrm dx \\ &= \int_0^1 {n-1 \choose i-1} x^i (1-x)^{n-i}\, \mathrm dx \\ &= {n-1 \choose i-1} \int_0^1 x^i (1-x)^{n-i}\, \mathrm dx \\ &= \frac{\Gamma(n)}{\Gamma(i) \cdot \Gamma(n-i+1)} \cdot \frac{\Gamma(i+1) \cdot \Gamma(n-i+1)}{ \Gamma(n+1) } \\ &= \frac{\Gamma(n)}{\Gamma(i) \cdot \Gamma(n-i+1)} \cdot \frac{i \cdot \Gamma(i) \cdot \Gamma(n-i+1)}{ (n+1) \cdot \Gamma(n) } = \frac{i}{n+1}. \end{aligned}$

Problem 2. Calculate the average number of rolls of a fair six-sided die that you need to roll in order for the sum of all rolls to be a multiple of $6$ .

(Click for Solution)

Solution. Let $\xi_i$ denote the $i$ -th roll and $X_n := \sum_{i=1}^n \xi_i$ denote the sum of the first $n$ rolls. Define the stopping time $N$ by

$latex\displaystyle N := \inf_{n \in \mathbb N} \{6 \mid X_n\}.$

We claim that $N \sim \mathrm{Geom}(1/6)$ . For any $n \in \mathbb N$ ,

$\{N = n\} = \{6 \nmid X_1, \dots, 6 \nmid X_{n-1}, 6 \mid X_n\}.$

For each $i$ ,

$\{ 6 \nmid X_{i-1}, 6 \mid X_i\} = \{ \xi_i = X_i - X_{i-1} \},$

which is one of the six possible numbers with equal probability:

$\mathbb P(N = n) = \mathbb P(\{6 \nmid X_1, \dots, 6 \nmid X_{n-1}, 6 \mid X_n\}) = (5/6)^{n-1} \cdot (1/6).$

Therefore, $N \sim \mathrm{Geom}(1/6)$ so that $\mathbb E[N] = 1/(1/6) = 6$ as well.

Problem 3. What is the probability of getting an odd number of heads out of $n$ independent flips of a fair coin?

(Click for Solution)

Solution. Let $X \sim \mathrm{Bin}(n, 1/2)$ denote the number of heads out of $n$ independent flips of a fair coin. Then the required probability is

$\begin{aligned} p_{\text{odd}} &= \sum_{k\, \text{odd}}^{n} \mathbb P(X = k) = \sum_{ k\, \text{odd} }^{ n } {n \choose k} \frac 1{2^n}. \end{aligned}$

Using properties involving the binomial coefficient,

$\begin{aligned} 0 = (1+(-1))^n &= \sum_{k=0}^n {n \choose k} (-1)^k \\ &= \sum_{k\, \text{odd}}^n {n \choose k} (-1)^k + \sum_{k\, \text{even}}^n {n \choose k} (-1)^k \\ &= \sum_{k\, \text{odd}}^n {n \choose k} \cdot (-1) + \sum_{k\, \text{even}}^n {n \choose k} \cdot 1 \\ &= -\sum_{k\, \text{odd}}^n {n \choose k} + \sum_{k\, \text{even}}^n {n \choose k}. \end{aligned}$

Therefore,

$\displaystyle \sum_{k\, \text{odd}}^n {n \choose k} = \sum_{k\, \text{even}}^n {n \choose k}.$

In particular,

$\begin{aligned} p_{\text{even}} &= \sum_{ k\, \text{even} }^{ n } {n \choose k} \frac 1{2^n} = p_{\text{odd}}. \end{aligned}$

Since $p_{\text{odd}} + p_{\text{even}} = 1$ , we must have $p_{\mathrm{odd}} = 1/2$ , as required.

Problem 4. Given $X_1, X_2 \sim \mathcal U(0, 1)$ , calculate $\mathbb E[\min\{X_1,X_2\}]$ .

(Click for Solution)

Solution. Denoting $Y = \min\{X_1, X_2\}$ , we observe that

$\displaystyle \mathbb P(Y > y) = \mathbb P(X_1 > y, X_2 > y) = \mathbb P(X_1 > y) \cdot \mathbb P(X_2 > y) = (1-y)^2.$

Therefore, by the tail integral for expectation,

$\begin{aligned} \mathbb E[Y] &= \int_0^1 \mathbb P(Y > y) \cdot \mathbb I_{[0, 1]}(y) \, \mathrm dy = \int_0^1 (1-y)^2\, \mathrm dy = \int_0^1 y^2\, \mathrm dy = 1/3. \end{aligned}$

Problem 5. You’re the second-best player in a single-elimination tournament with $2^n$ players. Assume the brackets are randomly seeded, and the better player always wins each match. What is the probability you reach the finals?

(Click for Solution)

Solution. Each tournament will have $n$ stages, and at stage $i$ , there will be $2^{n+1-i}$ players. In order to reach the final stage, we need to be in a different “bracket” with the best player. At stage $1$ , there are two “brackets”, and each bracket has $2^{n-1}$ players. Therefore, the required probability is

$\displaystyle \frac{2^{n-1}}{2^n - 1}.$

Problem 6. Consider the sample space $\{0, 1\}$ and the sequence of random variables $X_0, X_1,\dots$ with the property that

$\mathbb P(X_{n+1} = 1 \mid X_n = 1) = p,\quad \mathbb P(X_{n+1} = 0 \mid X_n = 0) = q.$

Assuming that $X_n$ has identical distribution, evaluate $\mathbb P(X_n = 1)$ .

(Click for Solution)

Solution. Denote $\mathbb P(X_n = 1) = s$ . By the law of total probability,

$\begin{aligned} \mathbb P(X_{n+1} = 1) &= \mathbb P(X_{n+1} = 1 \mid X_n = 1) \cdot \mathbb P(X_n = 1) \\ &\phantom{==} + \mathbb P(X_{n+1} = 1 \mid X_n = 0) \cdot \mathbb P(X_n = 0) \\ s &= p \cdot s + (1 - q) \cdot (1-s) \\ (1- p) \cdot s &= (1-q) - (1-q) \cdot s \\ (2 - p - q) \cdot s &= 1 - q \\ s &= \frac{1-q}{2-p-q}. \end{aligned}$

—Joel Kindiak, 17 Oct 25, 1947H

December 19, 2025
Counting Arguments

Recall that the quantity $\displaystyle {n \choose r}$ was defined inductively using Pascal’s identity

$\displaystyle {n \choose r} = {n-1 \choose r} + {n-1 \choose r-1}.$

and denotes the number of $r$ -subsets of a set of size $n$ (i.e. $n$ distinct objects).

Problem 1. Prove that $\displaystyle {n \choose r} = {n \choose n-r}$ .

(Click for Solution)

Solution. Fix a set of $n$ distinct objects. There are $\displaystyle {n \choose r}$ possible $r$ -subsets of items that we can remove from that set. Therefore, every $(n-r)$ -subset of items left behind is obtained by exactly one corresponding $r$ -subset of items removed. Therefore, the number of $(n-r)$ -subsets (left behind) equals the number of $r$ -subsets (removed), yielding

$\displaystyle {n \choose r} = {n \choose n-r}.$

Problem 2. Prove that $\displaystyle {n \choose m} {m \choose r} = {n \choose r} {n-r \choose m-r}$ .

(Click for Solution)

Solution. We can interpret the identity as counting the number of $m$ -committeees out of $n$ persons, and among the $m$ persons, we choose $r$ persons in a “core team”. This is the quantity counted by the left-hand side:

$\displaystyle {n \choose m} {m \choose r}.$

On the right-hand side, we count the same quantity differently: first choose the $r$ “core team” members, then choose the remaining $(m-r)$ members out of the remaining $(n-r)$ persons:

$\displaystyle {n \choose r} {n-r \choose m-r}.$

Since both types of counting give the same total,

$\displaystyle {n \choose m} {m \choose r} = {n \choose r} {n-r \choose m-r}.$

Problem 3. Prove that $\displaystyle {n \choose r} = \frac nr {n-1 \choose r-1}$ .

(Click for Solution)

Solution. Replacing $(n,m,r)$ with $(n,r,1)$ in Problem 2,

$\displaystyle r \cdot {n \choose r} = {n \choose r} {r \choose 1} = {n \choose 1} {n-1 \choose r-1} = n \cdot {n-1 \choose r-1}.$

Problem 4. Prove that $\displaystyle {n \choose r} = \frac {n}{n-r} {n-1 \choose r}$ .

(Click for Solution)

Solution. Using Problems 1 and 3,

$\displaystyle {n \choose r} = {n \choose n-r} = \frac{n}{n-r} \cdot {n-1 \choose n-r-1} = \frac{n}{n-r} \cdot {n-1 \choose r}.$

Problem 5. Prove that $\displaystyle {n \choose r} = \frac {n-r+1}r {n \choose r-1}$ .

(Click for Solution)

Solution. Replacing $(n,m,r)$ with $(n,r,r-1)$ in Problem 2,

$\begin{aligned} r \cdot {n \choose r} ={n \choose r} {r \choose r-1} &= {n \choose r-1} {n-(r-1) \choose r-(r-1)} \\ &= (n-r+1) \cdot {n \choose r-1}. \end{aligned}$

Problem 6. For any $n \in \mathbb N^+, r \in \mathbb N_0$ , count the number of $n$ -tuples $(x_1,\dots,x_n) \in \mathbb N_0^n$ such that

$\displaystyle \sum_{k=1}^n x_k = r.$

(Click for Solution)

Solution. Consider a row of $r$ stars and $(n-1)$ bars. Let $x_1$ denote the number of stars before the 1st bar, $x_2$ denote the number of stars after the 1st bar and before the 2nd bar, and so on and so forth. Each arrangement of the $r$ stars and $(n-1)$ bars then corresponds to each desired $n$ -tuple. Thus, the required number is the number of places to place the bars:

$\displaystyle {r + (n-1) \choose (n-1)} = {n+r-1 \choose n-1} ={n+r-1 \choose r}.$

Problem 7. For any $n \in \mathbb N^+, p \in \mathbb N_0$ , suppose $p$ is prime. Count the number of $(2n)$ -tuples $(x_1,\dots,x_n,y_1,\dots, y_n) \in \mathbb N_0^n$ such that

$\displaystyle \left( \sum_{i=1}^n x_i \right) \cdot \left( \sum_{j=1}^n y_j \right) = p.$

(Click for Solution)

Solution. Since $p$ is prime, we require one of the sums to equal $1$ , and the other to equal $p$ . If the $x_i$ terms sum to $1$ , then there are a total of $n$ possible options of $(x_1,\dots, x_n)$ . By Problem 6, there are a total of

$\displaystyle {n+p-1 \choose p}$

options of $(y_1,\dots, y_n)$ . By symmetry, the required total is

$\displaystyle 2n \cdot {n+p-1 \choose p}.$

—Joel Kindiak, 31 Jul 25, 2114H

December 16, 2025

Blog at WordPress.com.

Loading Comments...

Write a Comment...

Email (Required)

Name (Required)

Website

Subscribe Subscribed
- KindiakMath
- Already have a WordPress.com account? Log in now.