Recall that for any metric space  , we can define open balls with centre
, we can define open balls with centre  and radius
and radius  by
by

We have previously seen that the collection  forms a topological basis for
forms a topological basis for 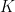 and induces the metric topology
and induces the metric topology  on
on 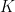 .
.
Problem 1. For any  , define the metric subspace
, define the metric subspace  by
by  . Prove that
. Prove that  coincides with the subspace topology of
coincides with the subspace topology of  .
.
(Click for Solution)
Solution. Regarding  as a topological subspace, the subspace topology is generated by a basis of the form
as a topological subspace, the subspace topology is generated by a basis of the form

On the other hand, the metric topology induced by  is generated by a basis of the form
is generated by a basis of the form

We aim to prove that  generates
generates  and
and  generates the subspace topology.
generates the subspace topology.
For the first claim, fix  and
and  . We seek
. We seek  such that
such that

Observe that for any  ,
,

Settin  yields the desired result. Hence,
yields the desired result. Hence,  generates
generates  .
.
For the second claim, fix any nonempty  and
and  , that is,
, that is,  and
and  . We seek
. We seek  such that
such that  . Now, for any
. Now, for any  ,
,

Setting  therefore yields the desired result. Hence,
therefore yields the desired result. Hence,  generates the subspace topology.
generates the subspace topology.
Problem 2. Prove that any inner product space  on
on  is also a metric space, with a metric induced by
is also a metric space, with a metric induced by  . Deduce that the map
. Deduce that the map  defined by
defined by

is a metric on  , called the Euclidean metric on
, called the Euclidean metric on  .
.
(Click for Solution)
Solution. The inner product induces a norm  on
on 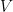 via the map
via the map  . The norm, in turn, induces a metric
. The norm, in turn, induces a metric  on
on 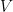 via the map
via the map  . For the final claim, we use the definition of the inner product on
. For the final claim, we use the definition of the inner product on  to deduce that
to deduce that

Problem 3. A function  is subadditive if
is subadditive if

Prove that  is subadditive.
is subadditive.
(Click for Solution)
Solution. For nonnegative 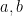 , since
, since  is bijective and non-decreasing,
is bijective and non-decreasing,

Taking square roots,  .
.
Problem 4. For metric spaces  and
and  and
and  , prove that the map
, prove that the map  defined by
defined by

is a metric on  .
.
(Click for Solution)
Solution. For the the nontrivial triangle inequality property, denote

We assert that  . By bookkeeping and using the triangle inequality for each
. By bookkeeping and using the triangle inequality for each 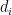 ,
,

By the Cauchy-Schwarz inequality,

Hence,

Taking square roots yields the desired result.
Problem 5. For metric spaces  and
and  and the metric
and the metric  on
on  as defined in Problem 4, prove that
as defined in Problem 4, prove that  coincides with the product topology on
coincides with the product topology on  .
.
(Click for Solution)
Solution. Recall that the product topology is generated by a basis given by

On the other hand, the topology generated by  has a basis of the form
has a basis of the form

We claim that  . To prove
. To prove  , fix
, fix  and any element
and any element  it contains. We seek
it contains. We seek  such that
such that

We observe that for any  ,
,

Hence, setting  yields the desired conclusion.
yields the desired conclusion.
To prove  , fix
, fix  and any element
and any element  it contains. We seek
it contains. We seek  such that
such that

We observe that for any  ,
,

Hence, setting  yields the desired conclusion.
yields the desired conclusion.
—Joel Kindiak, 28 Mar 25, 1538H
be continuous. For each
, define
. Prove that the set
,
and suppose
. Since
is bounded, by the Bolzano-Weierstrass theorem, it contains a convergent subsequence
. Hence, for any
, since
is continuous,
, as required.
. We will consider
equipped with the supremum metric (thus inducing the box topology) for computational simplicity. Fix
to be tuned. For each
, there exists
such that
denote the supremum metric. Since
forms an open cover for the compact space
, we can extract a finite sub cover
, where we denoted
for brevity.
. Now fix
and suppose
.
such that
and applying the triangle inequality yields
is compact. Hence, every sequence
in
has a convergent subsequence.