Any Taylor-based calculus joke links to the Taylor series. This is an incredibly powerful technique to approximate non-polynomial functions like  using polynomials.
using polynomials.
For this post, we will establish the existence of a Taylor series centred at 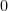 , known as a Maclaurin series.
, known as a Maclaurin series.
Definition. Define the  -th derivative of
-th derivative of  by
by

Theorem 1 (Taylor’s Theorem). Suppose  is a real-valued function that is
is a real-valued function that is  -times differentiable (that is,
-times differentiable (that is,  exists for
exists for  on
on  ). Then for any
). Then for any  , there exists
, there exists  such that
such that
 .
.
More concisely by using summation notation,

Before we prove the result, we observe that the case 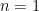 is the vanilla mean value theorem. Furthermore, we actually need to use this special case to prove the general case.
is the vanilla mean value theorem. Furthermore, we actually need to use this special case to prove the general case.
Proof. Fix  . Define
. Define  by
by

This ensures that

Define the  -differentiable function
-differentiable function ![g : [0, x] \to \mathbb R](https://s0.wp.com/latex.php?latex=g+%3A+%5B0%2C+x%5D+%5Cto+%5Cmathbb+R&bg=ffffff&fg=000&s=0&c=20201002) by
by

Direct substitutions yield  . Apply the mean value theorem to
. Apply the mean value theorem to  to find
to find  such that
such that

Apply the mean value theorem  more times to find
more times to find  such that
such that

Apply the mean value theorem one last time to find  such that
such that

Back-substituting yields

To use this theorem we need to ensure that  as
as 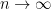 . One way that works is if there exists
. One way that works is if there exists  such that for any
such that for any  and for any
and for any  ,
,  , since
, since

where  can be established using real-analytic techniques. This criterion works well in the case of the exponential function.
can be established using real-analytic techniques. This criterion works well in the case of the exponential function.
Theorem 2. For any  ,
,

This is the Maclaurin series of 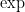 .
.
Proof. We will suppose  for simplicity. Using
for simplicity. Using  , for any integer
, for any integer  ,
,  and for any
and for any  ,
,  .
.
Similarly, we can establish the Maclaurin series for  and
and 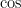 .
.
Theorem 3. For any  ,
,

Finally, we can formulate the general Taylor series based on the Maclaurin series.
Theorem 4 (Taylor’s Theorem). Suppose  is a real-valued function that is
is a real-valued function that is  -times differentiable. Then for any
-times differentiable. Then for any  , there exists
, there exists  such that
such that

Proof. Apply the vanilla Taylor’s theorem to the transformed function  .
.
—Joel Kindiak, 22 Oct 24, 1517H
be differentiable on
and
such that
.
for sufficiently large
.
identically, then
, and in particular,
. Now suppose
. Then there exists
such that
. By applying subsequent arguments on
, we may assume without loss of generality that
.
. Use the limits to find
such that
. Apply the intermediate value theorem on the intervals
and
respectively to find
and
such that
such that
, as required.