Tag: Probability

The Indicator Function
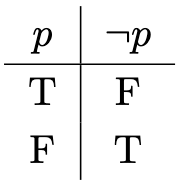
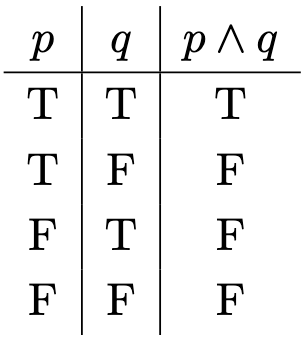
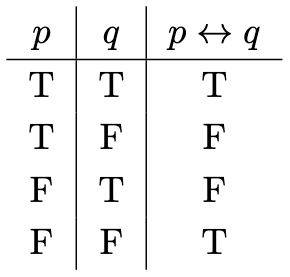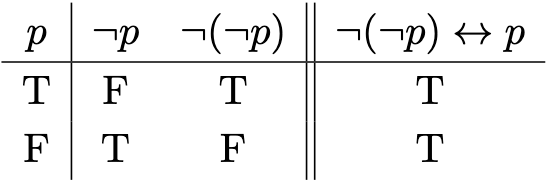Definition 1. Let $\Omega$ be any set. For any $K \subseteq \Omega$ , define the indicator function $\mathbb I_K : \Omega \to \{0, 1\} \subseteq \mathbb N_0$ on $K$ by

$\mathbb I_K(\omega) = \begin{cases} 1, & \omega \in K, \\ 0, & \omega \notin K. \end{cases}$

Example 1. We have $\mathbb I_{\Omega} = 1$ and $\mathbb I_{\emptyset} = 0$ .

Problem 1. Prove that the following propositions:
- $\mathbb I_K^{-1}(\{1\}) = K$ .
- $K = L \iff \mathbb I_K = \mathbb I_L$ .
(Click for Solution)

Solution. By definition,

$\omega \in K \iff \mathbb I_K(\omega) = 1 \iff \omega \in \mathbb I_K^{-1}(\{1\}).$

Therefore,

$\begin{aligned} K = L \quad &\Rightarrow \quad \mathbb I_K = \mathbb I_L \\ &\Rightarrow \quad \mathbb I_K^{-1}(\{1\}) = \mathbb I_L^{-1}(\{1\}) \\ &\Rightarrow \quad K = L.\end{aligned}$

Problem 2. Prove the following propositions:
- $\mathbb I_{K \cap L} = \mathbb I_{K} \cdot \mathbb I_{L}$ ,
- $\mathbb I_{\overline K} = 1 - \mathbb I_{K}$ , where $\overline K:= \Omega \backslash K$ ,
- $\mathbb I_{K \cup L} =\mathbb I_{K} + \mathbb I_{L} - \mathbb I_{K \cap L}$ .
(Click for Solution)

Solution. The proofs of the various equalities are straightforward applications of the definition of the indicator function.

For the first result, fix $\omega \in \Omega$ . If $\omega \in K \cap L \subseteq K$ , then $\mathbb{I}_{K \cap L}(\omega) = 1$ and $\mathbb{I}_{K}(\omega) = 1$ . Similarly, $\mathbb I_L(\omega) = 1$ . Hence,

$\mathbb{I}_{K \cap L}(\omega) = 1 = 1 \cdot 1 = \mathbb{I}_{K}(\omega)\mathbb{I}_{L}(\omega).$

The second result follows from $\omega \in \overline K \iff \omega \notin K \iff \mathbb I_K(\omega) = 0$ .

The third result follows from case splitting:

Suppose $\omega \in K$ and $\omega \in L$ . Then $\omega \in K \cap L$ , so that

$\mathbb I_{K}(\omega) + \mathbb I_{L}(\omega) - \mathbb I_{K \cap L}(\omega) = 1 + 1 - 1 = 1.$

In all other cases, $\mathbb I_{K \cap L}(\omega) = 0$ .

If $\omega \in K$ and $\omega \notin L$ , then

$\mathbb I_{K}(\omega) + \mathbb I_{L}(\omega) - \mathbb I_{K \cap L}(\omega) = 1 + 0 - 0 = 1.$

If $\omega \notin K$ and $\omega \in K$ , then

$\mathbb I_{K}(\omega) + \mathbb I_{L}(\omega) - \mathbb I_{K \cap L}(\omega) = 0 + 1 - 0 = 1.$

If $\omega \notin K$ and $\omega \notin L$ , then

$\mathbb I_{K}(\omega) + \mathbb I_{L}(\omega) - \mathbb I_{K \cap L}(\omega) = 0 + 0 - 0 = 0.$

Therefore, $\mathbb I_{K \cup L} =\mathbb I_{K} + \mathbb I_{L} - \mathbb I_{K \cap L}$ .

Problem 3. Use the previous problems to deduce the following set identities.
- $K \cap \emptyset = \emptyset$ ,
- $K \cap K = K$ ,
- $K \cap \Omega = K$ ,
- $K \cap L = L \cap K$ ,
- $K \cap (L \cap M) = (K \cap L) \cap M$ .
(Click for Solution)

Solution. By Problem 1, for each equality of the form $K_1 = K_2$ , it suffices to prove that $\mathbb I_{K_1} = \mathbb I_{K_2}$ :
- $\mathbb I_{K \cap \emptyset} = \mathbb I_K \cdot \mathbb I_{\emptyset} = \mathbb I_K \cdot 0 = 0 = \mathbb I_{\emptyset}$ ,
- $\mathbb I_{K \cap \Omega} = \mathbb I_K \cdot \mathbb I_{\Omega} = \mathbb I_K \cdot 1 = \mathbb I_K$ ,
- $\mathbb I_{K \cap K} = \mathbb I_K \cdot \mathbb I_K = \mathbb I_K$ since $0 \cdot 0 = 0$ and $1 \cdot 1 = 1$ ,
- $\mathbb I_{K \cap L} = \mathbb I_K \cdot \mathbb I_L = \mathbb I_L \cdot \mathbb I_K = \mathbb I_{L \cap K}$ .
The fifth result is slightly longer, but not too difficult to verify:

$\begin{aligned} \mathbb I_{K \cap (L \cap M)} &= \mathbb I_K \cdot \mathbb I_{L \cap M} \\ &= \mathbb I_K \cdot (\mathbb I_L \cdot \mathbb I_M) \\ &= (\mathbb I_K \cdot \mathbb I_L) \cdot \mathbb I_M \\ &= \mathbb I_{K \cap L} \cdot \mathbb I_M = \mathbb I_{(K \cap L) \cap M}. \end{aligned}$
Problem 4. Prove the following distributivity property

$K \cap (L \cup M) = (K \cap L) \cup (K \cap M).$

(Click for Solution)

Solution. We first observe that

$(K \cap L) \cap (K \cap M) = (K \cap K) \cap (L \cap M) = K \cap (L \cap M).$

Applying Problem 1 and Problem 2,

$\begin{aligned} \mathbb I_{K \cap (L \cup M)} &= \mathbb I_K \cdot \mathbb I_{L \cup M} \\ &= \mathbb I_K \cdot ( \mathbb I_L + \mathbb I_M - \mathbb I_{L \cap M} ) \\ &= \mathbb I_K \cdot \mathbb I_L + \mathbb I_K \cdot \mathbb I_M - \mathbb I_K \cdot \mathbb I_{L \cap M} \\ &= \mathbb I_K \cdot \mathbb I_L + \mathbb I_K \cdot \mathbb I_M - \mathbb I_{K \cap (L \cap M)} \\ &= \mathbb I_{K \cap L} + \mathbb I_{K \cap M} - \mathbb I_{(K \cap L) \cap (K \cap M)} \\ &= \mathbb I_{(K \cap L) \cup (K \cap M)}. \end{aligned}$

Problem 5. Prove the following propositions:
- $K = L \iff \overline K = \overline L$ ,
- $\overline{\overline K} = K$ ,
- $\overline{K \cup L} = \overline K \cap \overline L$ ,
- $\overline{K \cap L} = \overline K \cup \overline L$ ,
- $K \backslash L = K \backslash (K \cap L)$ ,
- $K \cap \overline K = \emptyset$ .
(Click for Solution)

Solution. By Problem 1,

$\begin{aligned}K = L \quad &\iff \quad \mathbb I_K = \mathbb I_L \\ &\iff \quad 1 - \mathbb I_K = 1 - \mathbb I_L \\ &\iff \quad \mathbb I_{\overline K} = \mathbb I_{\overline L} \\ &\iff \quad \overline K = \overline L. \end{aligned}$

For the second result,

$\mathbb I_{ \overline{\overline K} } = 1 - \mathbb I_{ \overline K } = 1 - (1 - \mathbb I_K) = \mathbb I_K.$

For the third result,

$\begin{aligned} \mathbb I_{ \overline{ K \cup L } } &= 1 - ( \mathbb I_K + \mathbb I_L - \mathbb I_{K \cap L} ) \\ &= 1 - \mathbb I_K - \mathbb I_L + \mathbb I_K \cdot \mathbb I_L \\ &= (1 - \mathbb I_K) \cdot (1 - \mathbb I_L) \\ &= \mathbb I_{ \overline K } \cdot \mathbb I_{ \overline L } = \mathbb I_{ \overline K \cap \overline L }. \end{aligned}$

For the fourth result,

$\overline{ \overline K \cup \overline L } = \overline{ \overline K } \cap \overline{ \overline L } = K \cap L.$

Therefore,

$\overline{ K \cap L } = \overline{ \overline{ \overline K \cup \overline L } } = \overline K \cup \overline L.$

For the fifth result,

$\begin{aligned} \mathbb I_{K \cap \overline K} &= \mathbb I_{K \backslash K} \\ &= \mathbb I_K - \mathbb I_{K \cap K} \\ &= \mathbb I_K - \mathbb I_K = 0 = \mathbb I_\emptyset. \end{aligned}$

For the sixth result,

$\begin{aligned} K \backslash (K \cap L) &= K \cap \overline{(K \cap L)} \\ &= K \cap (\overline K \cup \overline L) \\ &= (K \cap \overline K) \cup (K \cap \overline L)\\ &= \emptyset \cup (K \cap \overline L) \\ &= K \cap \overline L = K \backslash L. \end{aligned}$

Problem 6. Use the previous problems to deduce the following set identities.
- $K \cup \emptyset = K$ ,
- $K \cup K = K$ ,
- $K \cup \Omega = \Omega$ ,
- $K \cup L = L \cup K$ ,
- $K \cup (L \cup M) = (K \cup L) \cup M$ .
(Click for Solution)

Solution. We use Problem 1, Problem 2, and Problem 5.
- $\mathbb I_{ K \cup \emptyset } = \mathbb I_K + \mathbb I_{ \emptyset } - \mathbb I_{ K \cap \emptyset } = \mathbb I_K + \mathbb I_{ \emptyset } - \mathbb I_{ \emptyset } = \mathbb I_K$ ,
- $\mathbb I_{ K \cup K } = \mathbb I_{ K } + \mathbb I_{ K } - \mathbb I_{ K \cap K } = \mathbb I_{ K } + \mathbb I_{ K } - \mathbb I_{ K } = \mathbb I_K$ ,
- $\mathbb I_{ K \cup \Omega } = \mathbb I_{ K } + \mathbb I_{ \Omega } - \mathbb I_{ K \cap \Omega } = \mathbb I_{ K } + \mathbb I_{ \Omega } - \mathbb I_{ K } = \mathbb I_\Omega$ ,
- $\mathbb I_{ \overline{K \cup L} } = \mathbb I_{ \overline K \cap \overline L } = \mathbb I_{ \overline L \cap \overline K } = \mathbb I_{ \overline{L \cup K} }$ .
The fifth identity takes a bit more effort, and is useful to analyse in the context of complements.

$\begin{aligned} \mathbb I_{\overline{ K \cup (L \cup M) }} &= \mathbb I_{ \overline K \cap \overline{ L \cup M } } \\ &= \mathbb I_{ \overline K \cap ( \overline L \cap \overline M ) } \\ &= \mathbb I_{ ( \overline K \cap \overline L ) \cap \overline M } \\ &= \mathbb I_{ \overline { K \cup L } \cap \overline M } = \mathbb I_{ \overline { (K \cup L ) \cup M } }. \end{aligned}$
Problem 7. Prove the distributivity properties:

$\begin{aligned} K \cap (L \cup M) &= (K \cap L) \cup (K \cap M), \\ K \cup (L \cap M) &= (K \cup L) \cap (K \cup M). \end{aligned}$

(Click for Solution)

Solution. The first identity is the content of Problem 4.

Applying Problem 5,

$\begin{aligned} \overline{ K \cup (L \cap M) } &= \overline K \cap \overline{L \cap M} \\ &= \overline K \cap (\overline L \cup \overline M) \\ &= (\overline K \cap \overline L) \cup (\overline K \cap \overline M) \\ &= ( \overline{K \cup L} ) \cup ( \overline{K \cup M} ). \end{aligned}$

Taking complements,

$\begin{aligned} K \cup (L \cap M) &= \overline{ ( \overline{K \cup L} ) \cup ( \overline{K \cup M} ) } \\ &= \overline{ ( \overline{K \cup L} ) } \cap \overline{ ( \overline{K \cup M} ) } \\ &= ( K \cup L ) \cap ( K \cup M ). \end{aligned}$

Problem 8. Prove that the following propositions are equivalent:
- $K \subseteq L$ ,
- $K \cap \overline L = \emptyset$ ,
- $K \cap L = K$ ,
- $K \cup L = L$ .
Furthermore, in this case, prove that $\mathbb I_{L \backslash K} = \mathbb I_L - \mathbb I_K$ .

(Click for Solution)

Solution. We first note that by propositional logic $K \subseteq L$ is equivalent to

$\overline K \cup L = \Omega.$

Taking complements, the first proposition implies the second via

$K \cap \overline L = \overline{ \overline K \cup L } = \overline{\Omega} = \emptyset.$

Recalling that $\Omega = L \cup \overline L$ , the second proposition implies the third via

$\begin{aligned} K &= K \cap \Omega \\ &= K \cap (L \cup \overline L) \\ &= (K \cap L) \cup (K \cap \overline L) \\ &= ( K \cap L ) \cup \emptyset \\ &= K \cap L. \end{aligned}$

Applying Problem 1 and Problem 2, the third proposition implies the fourth via

$\begin{aligned} \mathbb I_{K \cup L} &= \mathbb I_K + \mathbb I_L - \mathbb I_{K \cap L} \\ &= \mathbb I_K + \mathbb I_L - \mathbb I_K = \mathbb I_L. \end{aligned}$

The fourth proposition implies the first via $K \subseteq K \cup L = L$ , since $\subseteq$ holds unconditionally via propositional logic.

Finally, by Problem 5, if $K \subseteq L$ , then

$\begin{aligned} \mathbb I_{L \backslash K} &= \mathbb I_L - \mathbb I_{L \cap K} \\ &= \mathbb I_L - \mathbb I_{K}. \end{aligned}$

Problem 9. Define the symmetric difference by

$K \oplus L := (K \backslash L) \cup (L \backslash K).$

Prove that $K \oplus L = (K \cup L) \backslash (K \cap L).$

(Click for Solution)

Solution. We first observe that

$\begin{aligned} \mathbb I_{(K \backslash L) \cap (L \backslash K)} &= \mathbb I_{K \backslash L} \cdot \mathbb I_{L \backslash K}\\ &= \mathbb I_{K \cap \overline L} \cdot \mathbb I_{L \cap \overline K} \\ &= \mathbb I_{K \cap \overline L \cap L \cap \overline K} \\ &= \mathbb I_{K \cap \overline K \cap L \cap \overline L} \\ &= \mathbb I_{\emptyset \cap \emptyset } = \mathbb I_{\emptyset } = 0.\end{aligned}$

Furthermore, $(K \cap L) \subseteq (K \cup L)$ implies

$\mathbb I_{(K \cup L) \backslash ( K \cap L ) } = \mathbb I_{K \cup L} - \mathbb I_{K \cap L}.$

Therefore,

$\begin{aligned}\mathbb I_{K \oplus L} &= \mathbb I_{(K \backslash L) \cup (L \backslash K)} \\ &= \mathbb I_{K \backslash L} + \mathbb I_{L \backslash K} - \mathbb I_{(K \backslash L) \cap (L \backslash K)} \\ &= \mathbb I_{K \cap \overline L} + \mathbb I_{L \cap \overline K} - 0 \\ &= \mathbb I_{K} \cdot \mathbb I_{\overline L} + \mathbb I_L \cdot \mathbb I_{\overline K} \\ &= \mathbb I_{K} \cdot (1 - \mathbb I_L) + \mathbb I_L \cdot(1 - \mathbb I_K) \\ &= \mathbb I_{K} - \mathbb I_{K} \cdot \mathbb I_{L} + \mathbb I_{L} - \mathbb I_{L} \cdot \mathbb I_{K} \\&= (\mathbb I_{K} + \mathbb I_{L} - \mathbb I_{K \cap L}) - \mathbb I_{K \cap L}\\ &= \mathbb I_{K \cup L} - \mathbb I_{K \cap L} \\ &= \mathbb I_{(K \cup L) \backslash ( K \cap L ) }. \end{aligned}$

—Joel Kindiak, 7 Feb 25, 1729H
February 18, 2025

geometry, machine-learning, math, mathematics, Probability
Calculus Recap (Polytechnic)

Limits

Problem 1. Evaluate the limit $\displaystyle \lim_{x \to 1} (x+1)$ .

(Click for Solution)

Solution. Substituting $x = 1$ ,

$\displaystyle \begin{aligned} \lim_{x \to 1} (x+1) &= 1 + 1 = 2. \end{aligned}$

Problem 2. Evaluate the limit $\displaystyle \lim_{x \to 1} \frac{x^2 - 1}{x-1}$ .

(Click for Solution)

Solution. Factorising for $x \neq 1$ ,

$\displaystyle \begin{aligned} \lim_{x \to 1} \frac{x^2 - 1}{x-1} &= \lim_{x \to 1} \frac{(x-1)(x+1)}{x-1} \\ &= \lim_{x \to 1} (x+1) = 2, \end{aligned}$

where the last $=$ follows from Problem 1.

Problem 3. Evaluate the limit $\displaystyle \lim_{x \to 1} \frac{\sqrt x - 1}{x-1}$ .

(Click for Solution)

Solution. Rationalising the numerator then substituting $x = 1$ ,

$\displaystyle \begin{aligned} \lim_{x \to 1} \frac{\sqrt x - 1}{x-1} &= \lim_{x \to 1} \frac{\sqrt x - 1}{x-1} \cdot \frac{\sqrt x + 1}{\sqrt x + 1} \\ &= \lim_{x \to 1} \frac{(\sqrt x)^2 - 1^2}{(x-1)(\sqrt x + 1)} \\ &= \lim_{x \to 1} \frac{x - 1}{(x-1)(\sqrt x + 1)} \\ &= \lim_{x \to 1} \frac 1{\sqrt x + 1} = \frac 1{\sqrt 1 + 1} = \frac 12.\end{aligned}$

Problem 4. Without using differentiation, compute the gradient of the tangent to $y =x^2$ at $(1, 1)$ .

(Click for Solution)

Solution. Denote $(x_1, y_1) = (1, 1)$ and $(x_2, y_2) = (x, x^2)$ . By definition of the gradient of the tangent,

$\displaystyle \begin{aligned} \lim_{x \to 1} \frac{\text{(rise)}}{\text{(run)}} &= \lim_{x \to 1} \frac{y_2 - y_1}{x_2 - x_1} = \lim_{x \to 1} \frac{x^2 - 1}{x - 1} = 2,\end{aligned}$

where the last $=$ follows from Problem 2.

Differentiation

Problem 5. Using differentiation, compute the gradient of the tangent to $y = x^2$ at $(1, 1)$ .

(Click for Solution)

Solution. Differentiating,

$\displaystyle \frac{\mathrm dy}{\mathrm dx} = \frac{\mathrm d}{\mathrm dx} (x^2) = 2x.$

Setting $x = 1$ , $\displaystyle \frac{\mathrm dy}{\mathrm dx} = 2 \cdot 1 = 2$ .

Problem 6. Defining $f(x) = x^2$ , evaluate $f''(1)$ .

(Click for Solution)

Solution. Differentiating twice,

$\begin{aligned} f(x) &= x^2, \\ f'(x) &= 2x, \\ f''(x) &= 2. \end{aligned}$

Setting $x = 1$ , $f''(1) = 2$ .

Problem 7. Evaluate $\displaystyle \frac{\mathrm d}{\mathrm dx}\left(\ln(x^2+9) \right)$ .

(Click for Solution)

Solution. Employing the chain rule,

$\displaystyle \begin{aligned} \frac{ \mathrm d }{ \mathrm dx }\left( \ln(x^2+1) \right) &= \frac 1{x^2 + 9} \cdot \frac{\mathrm d}{\mathrm dx}(x^2 + 1) \\ &= \frac 1{x^2 + 9} \cdot 2x \\ &= \frac { 2x }{x^2 + 9}. \end{aligned}$

Problem 8. Evaluate $\displaystyle \frac{\mathrm d}{\mathrm dx}\left(\sin \left(\ln(x^2+9) \right) \right)$ .

(Click for Solution)

Solution. Employing the chain rule and Problem 7,

$\displaystyle \begin{aligned} \frac{\mathrm d}{\mathrm dx}\left(\sin \left(\ln(x^2+1) \right) \right) &= \cos\left(\ln(x^2+9) \right) \cdot \frac{\mathrm d}{\mathrm dx}\ln(x^2+9) \\ &= \cos\left(\ln(x^2+9) \right) \cdot \frac {2x}{x^2 + 9} \\ &= \frac {2x \cos\left(\ln(x^2+9) \right) }{x^2 + 9}. \end{aligned}$

Problem 9. Evaluate $\displaystyle \frac{\mathrm d}{\mathrm dx} \left( (\ln x) \cdot (x^2 + 9) \right)$ .

(Click for Solution)

Solution. Employing the product rule,

$\displaystyle \begin{aligned} \frac{\mathrm d}{\mathrm dx} \left( (\ln x) \cdot (x^2 + 9) \right) &= (x^2 + 9) \cdot \frac{\mathrm d}{\mathrm dx} ( \ln x ) + \ln x \cdot \frac{\mathrm d}{\mathrm dx} (x^2 + 9) \\ &= (x^2 + 9) \cdot \frac 1x + \ln x \cdot (2x) \\ &= x + \frac 9x + 2x \ln x. \end{aligned}$

Problem 10. Evaluate $\displaystyle \frac{\mathrm d}{\mathrm dx} \left( \frac{\ln x}{x^2 + 9}\right)$ .

(Click for Solution)

Solution. Employing the quotient rule,

$\displaystyle \begin{aligned} \frac{\mathrm d}{\mathrm dx} \left( \frac{\ln x}{x^2 + 9} \right) &= \frac{(x^2 +9) \cdot \frac{\mathrm d}{\mathrm dx} ( \ln x ) - \ln x \cdot \frac{\mathrm d}{\mathrm dx} (x^2 + 9) }{(x^2 + 9)^2} \\ &= \frac{ (x^2 + 9) \cdot \frac 1x - \ln x \cdot 2x}{(x^2 + 9)^2 } \\ &= \frac{x^2 + 9 -2x^2 \ln x}{x(x^2 + 9)^2}. \end{aligned}$

Integration

Problem 11. Evaluate $\displaystyle \int \left(2\ln x + \frac 5{x^2+9}\right)\, \mathrm dx$ .

(Click for Solution)

Solution. Applying the linearity of integration and using common formulas (here and here),

$\displaystyle \begin{aligned} \int \left(2\ln x + \frac 5{x^2+9}\right)\, \mathrm dx &= \int \left(2 \cdot\ln x + 5 \cdot \frac 1{x^2 + 9}\right)\, \mathrm dx \\ &= 2 \cdot \int \ln x \, \mathrm dx + 5 \cdot \int \frac 1{3^2 + x^2} \, \mathrm dx \\ &= 2 \cdot (x \ln x - x) + 5 \cdot \frac 1{3} \tan^{-1} \left(\frac x3 \right) + C \\ &= 2x \ln x - 2x + \frac 53 \tan^{-1} \left(\frac x3 \right) + C. \end{aligned}$

Problem 12. Evaluate $\displaystyle \int_1^2 x\ln (x^2+9)\, \mathrm dx$ .

(Click for Solution)

Solution. Making the substitution $\displaystyle u = x^2 + 9 \Rightarrow \mathrm du = 2x\, \mathrm dx$ ,

$\displaystyle \begin{aligned} \int x\ln (x^2+9 )\, \mathrm dx &= \frac 12 \int \ln (x^2+9 ) \cdot 2x\, \mathrm dx \\ &= \frac 12 \int \ln u \, \mathrm du \\ &= \frac 12 (u \ln u - u) + C \\ &= \frac 12 \left((x^2 + 9) \ln (x^2 + 9) - (x^2 + 9) \right) + C. \end{aligned}$

Hence, substituting the limits,

$\displaystyle \begin{aligned} \int_1^2 x\ln (x^2+1)\, \mathrm dx &= \left[ \frac 12 \left( (x^2 + 9) \ln (x^2 + 9) - (x^2 + 9) \right) \right]_1^2 \\ &= \frac 12 \left( 13 \ln 13 - 13 \right) - \frac 12 \left( 10 \ln 10 - 10 \right) \\ &= \frac {13}2 \ln 13 - 5 \ln 10 - \frac 32.\end{aligned}$

Problem 13. Evaluate $\displaystyle \int \tan^3 x\, \mathrm dx$ .

(Click for Solution)

Solution. We solved this before, and solve it again for revision. Using the Pythagorean identity $\sec^2 x = \tan^2 x +1$ ,

$\displaystyle \begin{aligned} \int \tan^3 x\, \mathrm dx &= \int \tan x \tan^2 x\, \mathrm dx \\ &= \int \tan x (\sec^2 x - 1)\, \mathrm dx \\ &= \int \tan x \sec^2 x \, \mathrm dx - \int \tan x\, \mathrm dx \\ &= \int \tan x \sec^2 x \, \mathrm dx -(- \ln|{\cos x}|) + C.\end{aligned}$

For the first integral, make the substitution $\displaystyle u = \tan x \Rightarrow \mathrm dx = \frac{1}{\sec^2 x}\, \mathrm du$ . Then

$\displaystyle \begin{aligned}\int \tan x \sec^2 x \, \mathrm dx &= \int u \sec^2 x \cdot \frac{1}{\sec^2 x}\, \mathrm du \\ &= \int u\, \mathrm du \\ &= \frac 12 u^2 + C\\ &= \frac 12 \tan^2 x + C.\end{aligned}$

Therefore, $\displaystyle \int \tan^3 x\, \mathrm dx = \frac 12 \tan^2 x + \ln|{\cos x}| + C.$

Problem 14. Evaluate $\displaystyle \int \ln (x^2+9)\, \mathrm dx$ .

(Click for Solution)

Solution. Writing $\ln (x^2+9) = 1 \cdot \ln (x^2+9)$ and integrating by parts,

$\displaystyle \begin{aligned} \int \ln (x^2+9)\, \mathrm dx &= \underbrace{x}_{\mathrm I} \cdot \underbrace{\ln (x^2+9)}_{\mathrm S} - \int \underbrace{x}_{\mathrm I} \cdot \underbrace{\frac{2x}{x^2+9}}_{\mathrm D}\, \mathrm dx \\ &= x \ln(x^2 + 9) - \int \frac{2x^2}{x^2 + 9}\, \mathrm dx \\ &= x \ln(x^2 + 9) - 2\int \frac{(x^2 + 9) - 9}{x^2 + 1}\, \mathrm dx \\ &= x \ln(x^2 + 9) - 2\int \left( 1 - 9 \cdot \frac{1}{3^2 + x^2}\right) \, \mathrm dx \\ &= x \ln(x^2 + 9) - 2 \left( x - 9 \cdot \frac 1{3} \tan^{-1} \left( \frac x3 \right) \right) + C\\ &= x \ln(x^2 + 9) - 2x + 6\tan^{-1} \left( \frac x3 \right) + C.\end{aligned}$

Problem 15. Evaluate $\displaystyle \int \frac {2x+5}{x(x^2+9)}\, \mathrm dx$ .

(Click for Solution)

Solution. If we can decompose the integrand into

$\displaystyle \frac {2x+5}{x(x^2+9)} = \frac Ax + \frac{Bx+C}{x^2+9},$

Then a bit of basic integration yields

$\displaystyle \begin{aligned} \int \frac {2x+5}{x(x^2+9)}\, \mathrm dx &= \int \left(\frac Ax + \frac{Bx+C}{x^2+9}\right)\, \mathrm dx \\ &= \int \left(A \cdot \frac 1x + \frac B2 \cdot \frac{2x}{x^2+9} + C \cdot \frac 1{x^2 + 9} \right)\, \mathrm dx \\ &= A \int \frac 1x\, \mathrm dx + \frac B2 \int \frac {2x}{x^2 + 1}\, \mathrm dx + C \int \frac 1{3^2 + x^2}\, \mathrm dx \\ &= A \ln|x| + \frac B2 \ln (x^2 + 1) + C \cdot \frac 13 \tan^{-1} \left(\frac x3 \right) + D. \end{aligned}$

It remains to complete the decomposition. Clearing denominators,

$\begin{aligned}\frac {2x+5}{x(x^2+9)} &= \frac Ax + \frac{Bx+C}{x^2+9} \\ 2x+5 &= \frac {Ax(x^2+9)}x + \frac{(Bx+C)x(x^2+9)}{x^2+9} \\ 2x+5 &= A(x^2 + 9) + (Bx + C)x\\ 2x+5 &= (A+B)x^2 + Cx + 9A.\end{aligned}$

Setting $x = 0$ yields $A = 5/9$ .

Comparing coefficients yields $B = -5/9$ , and $C = 2$ .

Hence, by back-substituting,

$\displaystyle \begin{aligned} \int \frac 1{x(x^2+9)}\, \mathrm dx &= \frac 59 \ln|x| - \frac 5{18} \ln (x^2 + 9) + \frac 23 \tan^{-1} \left(\frac x3 \right) + C. \end{aligned}$

Problem 16. Evaluate $\displaystyle \int \frac {(2 \sin \theta +5)\cos \theta}{\sin \theta (\sin^2 \theta+9)}\, \mathrm d\theta$ .

(Click for Solution)

Solution. Making the substitution $\displaystyle u = \sin \theta \Rightarrow \mathrm d\theta = \frac{1}{\cos \theta}\, \mathrm du$ and applying the result from Problem 15,

$\displaystyle \begin{aligned} & \int \frac {(2 \sin \theta +5)\cos \theta}{\sin \theta (\sin^2 \theta+9)}\, \mathrm dx \\ &= \int \frac {(2u+5)\cos \theta}{u (u^2+9)} \cdot \frac{1}{\cos \theta}\, \mathrm du \\ &= \int \frac {2u+5}{u (u^2+9)} \, \mathrm du \\ &= \frac 59 \ln|u| - \frac 5{18} \ln (u^2 + 9) + \frac 23 \tan^{-1} \left(\frac u3 \right) + C \\ &= \frac 59 \ln| {\sin \theta} | - \frac 5{18} \ln ( \sin^2 \theta + 9 ) + \frac 23 \tan^{-1} \left(\frac {\sin \theta}3 \right) + C. \end{aligned}$

—Joel Kindiak, 13 Feb 25, 1757H

February 13, 2025

Calculus, math, mathematics, physics, Probability
Several Limit Comparisons

Problem 1. Prove that $n^{1/n} \to 1$ as $n \to \infty$ .

Solution. We refer to this solution for inspiration.

It suffices to prove that $x_n := n^{1/n} - 1 \to 0$ . We first check that $x_n \geq 0$ since taking $n$ -th roots to the inequality $n \geq 1$ yields $n^{1/n} \geq 1^{1/n} = 1$ . We then employ the binomial theorem to obtain

$\displaystyle n = (1 + x_n)^n \geq 1 + nx_n + \frac{n(n-1)}{2} x_n^2 \geq \frac{n(n-1)}{2} x_n^2.$

By algebra,

$\displaystyle 0 \leq x_n^2 \leq \frac{2}{n-1}.$

Since $2/(n-1) \to 0$ , by the squeeze theorem, $x_n^2 \to 0$ , so that $x_n \to 0$ , as required.

Problem 2. Prove that for any sequence $x_n > 0$ , if $x_{n+1}/x_n \to x$ for some $0 \leq x < 1$ , then $x_n \to 0$ .

Solution. Fix $\epsilon = 1$ . Since $x_{n+1}/x_n \to x$ , for any $k> 0$ , there exists $N \in \mathbb N$ such that for $n \geq N$ ,

$\displaystyle \left| \frac{x_{n+1}}{x_n} - x \right| <k \cdot \epsilon.$

By algebra, $x_{n} < (x + k) \cdot x_{n-1}$ . Set $k := (1-x)/2$ so that $r := x+ k < 1$ . Then

$\displaystyle 0\leq x_{n} < rx_{n-1}< \cdots < r^{n-N} x_N= \frac{x_N}{r^{N}} \cdot r^n \to 0.$

By the squeeze theorem, $x_n \to 0$ , as required.

Problem 3. For non-negative functions $f, g$ such that $f(n) \to \infty$ and $g(n) \to \infty$ , denote $f \ll g$ to mean that as $n \to \infty$ , $f(n)/ g(n) \to 0$ .

For non-negative functions $f,g,h$ , prove that if $f \ll g$ and $g \ll h$ , then $f \ll h$ . In this regard we can write $f \ll g \ll h$ without contradiction.

Solution. Assume $f(n),g(n),h(n) \geq 1 > 0$ for large $n$ . We observe that

$\displaystyle \frac{f(n)}{h(n)} = \frac{f(n)}{g(n)} \cdot \frac{g(n)}{h(n)} \to 0 \cdot 0 = 0,$

so that $f \ll h$ , as required.

Problem 4. Fix $k > 1$ and $a > 1$ . Prove that $n^k \ll a^n$ .

Solution. Define $x_n := n^k/a^n$ . We observe that

$\displaystyle \begin{aligned} \frac{x_{n+1}}{x_n} &= \frac{(n+1)^k/a^{n+1}}{n^k/a^n} = \left(1 + \frac 1n\right)^k \cdot \frac 1a \to (1+0)^k \cdot \frac 1a = \frac 1a < 1.\end{aligned}$

By Problem 2, $x_n \to 0$ , which implies $n^k \ll a^n$ .

Problem 5. Fix $k > l > 1$ and $b > a > 1$ . Prove the common comparisons

$\log n \ll n \ll n \log n \ll n^k \ll n^l \ll a^n \ll b^n \ll n! \ll n^n.$

Here, $\log \equiv \ln$ by conventional mathematical notation.

Solution. To prove $\log n \ll n$ , we observe that by Problem 1,

$\displaystyle \begin{aligned} \frac{\log n}{n} &= \log (n^{1/n}) \to \log(1) = 0. \end{aligned}$

$n \ll n \log n$ is obvious since $1/{\log n} \to 0$ . Next, since $\log n \ll n$ ,

$\displaystyle \frac{ n \log n }{ n^k } = \frac{ \log n }{ n^{k-1} } = \frac 1{k-1} \cdot \frac{ \log(n^{k-1}) }{ n^{k-1} } \to \frac 1{k-1} \cdot 0 = 0.$

To prove $b^n \ll n!$ , define $x_n := b^n/n!$ . Then

$\displaystyle \frac{x_{n+1}}{x_n} = \frac{b}{n+1} \to 0 < 1,$

so that $x_n \to 0$ implies $b^n \ll n!$ . The final result follows from

$\displaystyle 0 \leq \frac{n!}{n^n} \leq \frac 1n \to 0.$

February 8, 2025

Calculus, math, mathematics, number-theory, Probability
Differential Equation Magic

Recall the method of separable variables, which solves

$\displaystyle \frac{\mathrm dy}{\mathrm dx} = f(x)g(y)$

by separating the $x$ from the $y$ , and integrating on both sides:

$\displaystyle \int \frac{1}{g(y)}\, \mathrm dy = \int f(x)\, \mathrm dx.$

In particular, we have solved the following equation in a similar manner.

Theorem 1. For any continuous $P$ , the general solution to the differential equation

$\displaystyle \frac{\mathrm dy}{\mathrm dx} + P(x)y = 0$

is given by $\displaystyle y = Ae^{-\int P(x)\, \mathrm dx}$ , where $A = \pm 1$ .

Proof. Exercise.

How do we solve more general equations? For instance, we want to solve the equation

$\displaystyle \frac{\mathrm dy}{\mathrm dx} + P(x)y = Q(x),$

where $P$ and $Q$ are continuous so that they can be integrated. There are multiple perspectives to approach this problem, but the approach we will take will connect this problem with the separable variables method.

Let’s first recall the product rule. Given any function $\mu(x)$ , the product rule tells us that

$\displaystyle \frac{\mathrm d}{\mathrm dx}(y \mu(x)) = \frac{\mathrm dy}{\mathrm dx} \mu(x) + y \mu'(x).$

Dividing by $\mu(x)$ yields

$\displaystyle \frac 1{\mu(x)} \cdot \frac{\mathrm d}{\mathrm dx}(y \mu(x)) = \frac{\mathrm dy}{\mathrm dx}+ \frac{\mu'(x)}{\mu(x)} y.$

Now, cue the key insight: If we specially chose some $\mu$ such that $\mu'(x)/\mu(x) = P(x)$ , then

$\displaystyle \frac 1{\mu(x)} \cdot \frac{\mathrm d}{\mathrm dx}(y \mu(x)) = \frac{\mathrm dy}{\mathrm dx}+ P(x) y = Q(x).$

Then doing a little bit of algebra and integration yields

$\displaystyle \begin{aligned}\frac 1{\mu(x)} \cdot \frac{\mathrm d}{\mathrm dx}(y \mu(x)) &= Q(x) \\ \frac{\mathrm d}{\mathrm dx}(y \mu(x)) &= \mu(x) Q(x) \\y \mu(x) &= \int \mu(x) Q(x)\, \mathrm dx. \end{aligned}$

We call $\mu(x)$ an integrating factor, since it is the factor multiplied to help us integrate the expression. What should $\mu \equiv \mu(x)$ be, though? Remember our key insight? Well, writing $\displaystyle \mu' = \frac{\mathrm d \mu}{\mathrm dx}$ ,

$\displaystyle \frac{\mathrm d\mu}{\mathrm dx} - P(x)\mu = 0.$

Then Theorem 1 gives us the result

$\displaystyle \mu = Ae^{-\int (-P(x))\, \mathrm dx} = Ae^{\int P(x)\, \mathrm dx},$

where $A$ is any arbitrary nonzero constant. Denote $\mu_0(x) = e^{\int P(x)\, \mathrm dx}$ so that $\mu = A \mu_0$ . Making the substitution,

$\displaystyle \begin{aligned} y \mu(x) &= \int \mu(x) Q(x)\, \mathrm dx\\ y \cdot A\mu_0(x) &= \int A\mu_0(x) Q(x)\, \mathrm dx \\ y \mu_0(x) &= \int \mu_0(x) Q(x)\, \mathrm dx \end{aligned}$

This means that $A$ eventually cancels out, and therefore without loss of generality, we can assume $\mu(x) = \mu_0(x) = e^{\int P(x)\, \mathrm dx}$ . This yields the method of integrating factors.

Theorem 2. For any continuous $P, Q$ , the general solution to the differential equation

$\displaystyle \frac{\mathrm dy}{\mathrm dx} + P(x)y = Q(x)$

is given by

$\displaystyle y \mu(x) = \int \mu(x) Q(x)\, \mathrm dx,\quad \mu(x) = e^{\int P(x)\, \mathrm dx}.$

Example 1. Given $\alpha \neq \beta$ , find the general solution to the differential equation

$\displaystyle \frac{\mathrm dy}{\mathrm dx} - \beta y = Ae^{\alpha x}.$

Solution. By the method of integrating factors, $P(x) = -\beta$ and $Q(x) = Ae^{\alpha x}$ . Then the integrating factor is given by

$\mu(x) = e^{\int P(x)\, \mathrm dx} = e^{\int -\beta\, \mathrm dx} = e^{-\beta x}.$

Thus, the general solution is given by

$\displaystyle \begin{aligned} y \mu(x) &= \int \mu(x) Q(x)\, \mathrm dx \\ y e^{-\beta x} &= \int e^{-\beta x} \cdot Ae^{\alpha x}\, \mathrm dx \\ &= \int A e^{(\alpha-\beta) x}\, \mathrm dx \\ &= \frac{A}{\alpha - \beta}\cdot e^{(\alpha-\beta) x} + C \\ y &= \frac{A}{\alpha - \beta}\cdot e^{(\alpha-\beta) x} \cdot e^{\beta x} + Ce^{\beta x} \\ &= \frac{A}{\alpha - \beta}\cdot e^{\alpha x}+ Ce^{\beta x} \\ &= C_1 e^{\alpha x} + C_2 e^{\beta x}, \end{aligned}$

where $C_1 := A/(\alpha - \beta), C_2 := C$ are arbitrary constants.

In fact, Example 1 is the key motivating result for us to study the next idea in a course in differential equations: second-order differential equations.

—Joel Kindiak, 27 Jan 25, 1712H

February 4, 2025

Calculus, math, mathematics, physics, Probability
The Beauty of Bounded Sequences

Sequences can converge, but they may not. That remains true with bounded sequences. Nevertheless, we do gain some convenient convergence properties from bounded sequences that are, in general, not guaranteed when sequences are not bounded.

Monotone Convergence Theorem. Let $\{x_n\}$ be a sequence that is bounded above (resp. bounded below) and non-decreasing (resp. non-increasing). Then $\{x_n\}$ converges.

Proof. Assume $\{x_n\}$ is bounded above and non-decreasing. Since $\{x_n\}$ is bounded above, let $M := \sup \{x_n\}$ . Fix $\epsilon > 0$ . By definition, there exists $N \in \mathbb N$ such that $x_N > M - \epsilon$ . Then, for $n > N$ ,

$M - \epsilon < x_N \leq x_n \leq M < M+ \epsilon \quad \Rightarrow \quad |x_n - M| <\epsilon.$

Therefore, $x_n \to M$ , so that $\{x_n\}$ converges. Now, if $\{x_n\}$ is bounded below, then $\{-x_n\}$ is bounded above. Thus, $-x_n \to L$ for some $L \in \mathbb R$ , so that $x_n \to -L$ . Thus, $\{x_n\}$ converges.

Bolzano-Weierstrass Theorem. Let $\{x_n\}$ be a bounded sequence. Then there exists an increasing sequence $\{n_k\}$ such that the subsequence $\{x_{n_k}\}$ converges.

Proof. We first remark that for nonempty sets $K, L$ that are bounded above (resp. bounded below), $K \subseteq L$ implies $\sup K \leq \sup L$ (resp. $\inf L \leq \inf K$ ). Since $\{x_n\}$ is bounded, $|x_n| \leq M$ for some $M > 0$ .

Call a number $x_n$ a peak term if $x_n = \sup\{x_k : k \geq n\}$ .

Suppose $\{ x_n \}$ has finitely many peak terms with the last peak term $x_N$ . Define $n_1 := N+1$ . Define inductively $n_{k+1}$ as follows: for $n_k > N$ , there exists $n_{k+1} > n_k$ such that $x_{n_k} < x_{n_{k+1}} \leq M$ . Therefore, we have defined a non-decreasing subsequence $\{x_{n_k}\}$ that is bounded above by $M$ . By the monotone convergence theorem, $\{x_{n_k}\}$ converges, and we are done.

Now suppose $\{x_n\}$ has infinitely many peak terms $x_{n_1},x_{n_2},\dots$ . By definition, $\{x_{n_k}\}$ is non-increasing. Since $\{ x_n \}$ is bounded below by $-M$ , so is $\{x_{n_k}\}$ . By the monotone convergence theorem again, $\{x_{n_k}\}$ converges, and we are done.

Corollary 1. Let $\{x_n\}$ be a bounded sequence in $[a, b]$ . Then $\{x_n\}$ contains a subsequence that converges in $[a, b]$ .

Proof. By the Bolzano-Weierstrass theorem, let $\{x_{n_k}\}$ be a convergent subsequence of $\{x_n\}$ with limit $x$ . We have

$\displaystyle a \leq x_{n_k} \leq b \quad \Rightarrow a \leq \underbrace{\lim_{k \to \infty} x_{n_k}}_x \leq b,$

so that $x \in [a, b]$ , as required.

January 22, 2025

Calculus, math, mathematics, Probability, Real Analysis
Several Integrable Combinations
Let $f, g : [a, b] \to \mathbb R$ be Riemann-integrable.

Problem 1. Prove that the following functions are Riemann-integrable:
- $f + g : [a, b]\to \mathbb R$ ,
- $cf : [a, b]\to \mathbb R$ for any $c \in \mathbb R$ .
Solution. We prove the first result. Fix $\epsilon > 0$ . For any $k_1, k_2 > 0$ , find partitions $P, Q \subseteq [a, b]$ with $R := P \cup Q$ such that

$\begin{aligned} U(f, R) - L(f, R) &< k_1 \cdot \epsilon \\ U(g, R) - L(g, R) &< k_2 \cdot \epsilon \end{aligned}$

By definition, on each $[x_{i-1}, x_i]$ ,

$\begin{aligned} m_i(f, R) \leq f \leq M_i(f, R) \\ m_i(g, R) \leq g \leq M_i(g, R) \end{aligned}$

Adding yields

$m_i(f, R) + m_i(g, R) \leq f+g \leq M_i(f,R) + M_i(g,R).$

Taking supremums and infimums yields

$\begin{aligned} m_i(f, R) + m_i(g, R) \leq m_i(f+g,R) \\ M_i(f+g,R) \leq M_i(f,R) + M_i(g,R) \end{aligned}$

Thus,

$\displaystyle \begin{aligned} & \sum_{i=1}^n (M_i(f+g,R) - m_i(f+g,R)) \\ &\leq (U(f, R) - L(f, R)) + (U(g, R) - L(g, R)) \\ &< (k_1 + k_2) \cdot \epsilon. \end{aligned}$

Setting $k_1 = k_2 = 1/2$ yields the desired result. We leave it as a bookkeeping exercise to verify that

$\displaystyle \int_a^b (f+g) = \int_a^b f + \int_a^b g.$

For the second result, the result is obvious with $c = 0$ . Follow a similar proof for $c > 0$ via the estimate

$M_i(cf, P) - m_i(cf, P) = c(M_i(f, P) - m_i(f, P)).$

For $c < 0$ , write $cf = -1 \cdot (-c)f$ . It suffices to establish the case $c = -1$ . The proof is almost identical with the exception that

$M_i(-f, P) = -m_i(f, P),\quad m_i(-f, P) = - M_i(f, P)$

so that

$M_i(-f, P) - m_i(-f, P) = M_i(f, P) - m_i(f, P).$

Finally we leave it as a bookkeeping exercise to verify that

$\displaystyle \int_a^b (cf) = c \int_a^b f.$

Problem 2. Prove that the following functions are Riemann-integrable:
- $f^2 : [a, b] \to \mathbb R$ ,
- $fg : [a, b] \to \mathbb R$ ,
- $|f| : [a, b] \to \mathbb R$ ,
- $f^+ := \max\{0, f\} : [a, b] \to \mathbb R$ ,
- $\max\{f, g\} : [a, b] \to \mathbb R$ .
Remarkably, closed forms for these functions in terms of $\displaystyle \int_a^b f, \int_a^b g$ are highly nontrivial.

Solution. We will establish these properties in sequence.
- Since $(\cdot)^2 : [0, \max f([a,b])] \to \mathbb R$ is continuous, $f^2 = (\cdot)^2 \circ f$ is Riemann-integrable.
- Then $fg = \frac 12 ((f+g)^2 - f^2 - g^2)$ is Riemann-integrable.
- Furthermore, $\sqrt{\cdot} : [0, \max |f([a,b])|] \to \mathbb R$ is continuous, $|f| = \sqrt{\cdot} \circ f^2$ is Riemann-integrable.
- Then $f^+ = \frac 12 (f + |f|)$ is Riemann-integrable.
- Finally, $\max\{f, g\} = f + \max\{0, g-f\}$ is Riemann-integrable.
Problem 3. Prove that $\displaystyle \left| \int_a^b f \right| \leq \int_a^b \left| f \right|$ .

Solution. Apply the monotonicity of integration to $0 \leq f + |f| \leq 2|f|$ .

Remark. If $f,g$ are Lebesgue-integrable implies that the following functions are Lebesgue-integrable:
- $f + g : [a, b]\to \mathbb R$ ,
- $cf : [a, b]\to \mathbb R$ for any $c \in \mathbb R$ ,
- $\phi \circ f : [a, b] \to \mathbb R$ , where $\phi$ is continuous,
then all the functions in Problem 2 will also be Lebesgue-integrable, and the estimate in Problem 3 still holds. In other words, Problem 1 together with closure under composition with a continuous function, if both still hold when “Riemann-integrable” is replaced with “Lebesgue-integrable” (more generally, any suitable predicate $\Phi$ on the set of functions $[a, b] \to \mathbb R$ ) will imply the desired Lebesgue-integrability properties in Problem 2 and Problem 3.

—Joel Kindiak, 21 Jan 25, 1736H
January 21, 2025

inequalities, math, mathematics, number-theory, Probability
Composing Integrability

In this question, we compose certain functions to preserve integrability.

Problem 1. Let $f : [a, b] \to \mathbb R$ be an integrable function, and suppose $m \leq f \leq M$ . Let $\phi : [m, M] \to \mathbb R$ be continuous. Prove that $\phi \circ f$ is integrable.

Solution. Fix $\epsilon > 0$ . Since $\phi$ is continuous, it is uniformly continuous. Thus, for any $k_1 > 0$ , there exists $\delta > 0$ such that for any $u,v \in [m,M]$ ,

$|u-v| < \delta \quad \Rightarrow \quad |\phi(u) - \phi(v)| < k_1 \cdot \epsilon.$

Since $f$ is integrable, for any $k_2 > 0$ , there exists a partition $P \subseteq [a, b]$ such that

$\displaystyle \sum_{i = 1}^{|P|} (M_i(f,P) - m_i(f,P))\Delta x_i = U(f, P) - L(f, P) < k_2 \cdot \epsilon.$

We need to treat the values $m_i(f,P)$ , $M_i(f, P)$ as inputs to $\phi$ . We observe that if $M_i(f,P) - m_i(f,P) < \delta$ , then for any $u,v \in [m_i(f, P), M_i(f, P)]$ , the continuity of $\phi$ yields

$|\phi(u) - \phi(v)| < k_1 \cdot \epsilon.$

Therefore, we will define the index sets

$\begin{aligned} A &:= \{i : M_i(f,P) - m_i(f,P) < \delta\}, \\ B &:= \{i : M_i(f,P) - m_i(f,P) \geq \delta\}. \end{aligned}$

For each $i$ ,

$\begin{aligned} M_i(\phi \circ f, P) - m_i(\phi \circ f, P) &= \sup_{u, v \in [x_{i-1}, x_i] } (\phi(u) - \phi(v)). \end{aligned}$

For $i \in A$ ,

$\displaystyle M_i(\phi \circ f, P) - m_i(\phi \circ f, P) \leq k_1 \cdot \epsilon.$

For $i \in B$ , since $\phi$ is bounded, suppose $|\phi| \leq K$ . Then

$\displaystyle M_i(\phi \circ f, P) - m_i(\phi \circ f, P) \leq 2K.$

Therefore,

$\displaystyle \begin{aligned} U(\phi \circ f, P) - L(\phi \circ f, P) &< \sum_{i \in A} (k_1 \cdot \epsilon) \cdot \Delta x_i + \sum_{i \in B} 2K \cdot \Delta x_i \\ &= (k_1 \cdot \epsilon) \cdot \sum_{i \in A} \Delta x_i + 2K \cdot \sum_{i \in B} \Delta x_i \\ &\leq (k_1 \cdot \epsilon) \cdot (b-a) + 2K \cdot \sum_{i \in B} \Delta x_i. \end{aligned}$

We have run into a problem. The first term can be controlled pretty well, but not the second. The key idea is to take advantage of the integrability of $f$ . Since each “height” is $\geq \delta$ and the region under $f$ has finite area, the total “width” needs to be tiny.

To synthesise this observation, we make the estimate

$\displaystyle \begin{aligned} k_2 \cdot \epsilon &> \sum_{i \in B} (M_i(f, P) - m_i(f, P)) \Delta x_i \\ &\geq \sum_{i \in B} \delta \cdot \Delta x_i \\ &= \delta \cdot \sum_{i \in B} \Delta x_i. \end{aligned}$

This yields the estimate

$\displaystyle \sum_{i \in B} \Delta x_i < \frac{k_2 \cdot \epsilon}{\delta}.$

Therefore,

$\displaystyle \begin{aligned} U(\phi \circ f, P) - L(\phi \circ f, P) &\leq (k_1 \cdot \epsilon) \cdot (b-a) + 2K \cdot \sum_{i \in B} \Delta x_i \\ &<(k_1 \cdot \epsilon) \cdot (b-a) + 2K \cdot \frac{k_2 \cdot \epsilon}{\delta} \\ &= \left(k_1 \cdot (b-a) + 2K \cdot \frac{k_2}{\delta}\right) \cdot \epsilon. \end{aligned}$

Taking care of the dependencies, setting $k_1 = 1/(2(b-a))$ , $k_2 = \delta/(4K)$ yields the desired result.

Problem 2. Construct an integrable function $f : [a, b] \to \mathbb R$ be an integrable function with $m \leq f \leq M$ and an integrable function $\phi : [m, M] \to \mathbb R$ such that $\phi \circ f$ is not integrable.

Solution. Letting $f : [0, 1] \to \mathbb R$ be the popcorn function and defining $\phi : [0, 1] \to \mathbb R$ by $\phi(x) = 0$ if $x = 0$ and $\phi(x) = 1$ otherwise. Both $f, \phi$ are integrable. Then $\phi \circ f = \mathbb I_{\mathbb Q} : [0, 1] \to \mathbb R$ is a bounded function known as the Dirichlet function. We claim that this function is not Riemann-integrable.

Let $\epsilon > 0$ be suitably chosen and $P = \{x_0,x_1,\dots,x_n\}$ be any partition of $[0, 1]$ . For each $i$ , since $\mathbb Q \cap [x_{i-1}, x_i]$ and $[x_{i-1}, x_i]\backslash \mathbb Q$ are both dense in $[x_{i-1}, x_i]$ , there exist $r \in \mathbb Q \cap [x_{i-1}, x_i]$ , $s \in [x_{i-1}, x_i]\backslash \mathbb Q$ , yielding

$\begin{aligned} 0 &\leq m_i(f, P) \leq f(s) = 0,\\ 1 &= f(r) \leq M_i(f, P) \leq 1.\end{aligned}$

so that $m_i(f, P) = 0$ , $M_i(f, P) = 1$ . Therefore,

$\begin{aligned} U(f, P) - L(f, P) &= \sum_{i =1}^n (M_i(f, P) - m_i(f,P))\Delta x_i \\ &= \sum_{i =1}^n (1 - 0)\Delta x_i \\ &= (1 - 0)\cdot \sum_{i =1}^n \Delta x_i \\ &= (1 - 0) \cdot 1 = 1. \end{aligned}$

Setting $\epsilon = 1/2 < 1$ yields the result that the Dirichlet function is not integrable.

—Joel Kindiak, 21 Jan 25, 0033H

January 20, 2025

analysis, machine-learning, math, mathematics, Probability
Mashed Potato Rationals

Definition 1. For sets $K, L \subseteq \mathbb R$ , we say that $K$ is dense in $L$ if for any $x,y \in L$ with $x < y$ , there exists $z \in K$ such that $x < z < y$ . For this definition, we do not assume $K \subseteq L$ .

Problem 1 (Density Theorem). Prove that $\mathbb Q$ is dense in $\mathbb R$ .

(Click for Solution)

Solution. Fix $x,y \in \mathbb R$ such that $x < y$ . Then $y-x > 0$ . By the Archimedean property, find $n \in \mathbb N$ such that

$\displaystyle 0 < \frac 1n < y-x \quad \Rightarrow \quad nx < nx + 1 < ny.$

Intuitively, there should be one integer between $nx$ and $nx + 1$ . To formulate this rigorously, the definition of the floor function $\lfloor \cdot \rfloor : \mathbb R \to \mathbb Z$ yields the estimate

$\lfloor nx \rfloor \leq nx < \lfloor nx \rfloor + 1.$

Hence,

$\displaystyle nx < \lfloor nx \rfloor +1 \leq nx + 1 < ny \quad \Rightarrow \quad x < \frac{\lfloor nx \rfloor+1}{n} < y.$

Set $z := (\lfloor nx \rfloor+1)/n \in \mathbb Q$ to obtain the desired result.

Problem 2. Prove that $\mathbb Q(\sqrt 2) := \{r\sqrt 2 : r \in \mathbb Q\}$ is dense in $\mathbb R$ .

(Click for Solution)

Solution. Fix $x,y \in \mathbb R$ such that $x < y$ . Dividing by $\sqrt 2$ yields $x/\sqrt 2 < y/\sqrt 2$ . By Problem 1, find a nonzero rational number $r$ such that

$\displaystyle \frac x{\sqrt 2} < r < \frac y{\sqrt 2}\quad \Rightarrow \quad x < r\sqrt 2 < y.$

Define $z := r\sqrt 2 \in \mathbb R \backslash \mathbb Q$ , as required.

Problem 3. Suppose $K \subseteq L$ and $K$ is dense in $M$ . Then $L$ is dense in $M$ .

(Click for Solution)

Solution. Fix $x,y \in M$ such that $x < y$ . Since $K$ is dense in $M$ , there exists $z \in K \subseteq L$ such that $x < z < y$ , as required.

Problem 4. Deduce that $\mathbb R \backslash \mathbb Q$ is dense in $\mathbb R$ .

(Click for Solution)

Solution. We claim that $\mathbb Q(\sqrt 2) \subseteq \mathbb R \backslash \mathbb Q$ , since $\sqrt{2} = (r\sqrt 2)/r$ (so that $r \sqrt 2 \in \mathbb Q \Rightarrow \sqrt 2 \in \mathbb Q$ , a contradiction).

By Problems 2 and 3, $\mathbb R \backslash \mathbb Q$ is dense in $\mathbb R$ .

Problem 5. Suppose $K$ is dense in $L$ and $L$ is dense in $M$ . Then $K$ is dense in $M$ .

(Click for Solution)

Solution. Fix $x,y \in M$ such that $x < y$ . Since $L$ is dense in $M$ , there exists $u \in L \subseteq M$ such that $x < u < y$ . Apply the density of $L$ in $M$ again to obtain $v \in L$ such that $u < v < y$ .

Since $K$ is dense in $L$ , there exists $z \in K$ such that $u < z < v$ . Therefore,

$x < u < z < v < y \quad \Rightarrow \quad x < z < y,$

as required.

Problem 6. Prove that for continuous functions $f, g : \mathbb R \to \mathbb R$ and $K$ dense in $L$ , if $f|_{K} = g|_{K}$ , then $f|_L = g|_L$ .

(Click for Solution)

Solution. Fix $x \in L$ . For each $n \in \mathbb N$ , since $K$ is dense in $L$ , find $x_n \in K$ such that $|x_n - x| < 1/n$ . Taking $n \to \infty$ , since $| \cdot |$ is continuous,

$\displaystyle \left| \lim_{n \to \infty} x_n - x \right| = \lim_{n \to \infty} |x_n - x| \leq \lim_{n \to \infty} \frac 1n = 0.$

Therefore, $x_n \to x$ , so that by the continuity of $f, g$ ,

$\displaystyle f(x) = \lim_{n \to \infty} f(x_n) = \lim_{n \to \infty} g(x_n) = g(x).$

Since $x \in L$ is arbitrary, $f|_L = g|_L$ .

Corollary 1. By Problem 1, $\mathbb Q$ is dense in $\mathbb R$ . Hence, by Problem 6, for any $a > 0$ , the continuous exponential $\exp_a$ with base $a > 0$ , defined by $\exp_a(x) := a^x$ , is unique.

—Joel Kindiak, 19 Jan 25, 1633H

January 19, 2025

geometry, math, mathematics, number-theory, Probability
The Logic of Logic
If pure mathematics is a language, then numbers and variables constitute letters, definitions constitute words, and theorems constitute short paragraphs, all building up to a unified story that explains the explanation for the world. What is its grammar? Logic.

Definition 1. A proposition is a sentence that is either true, denoted $\mathrm T$ , or not, denoted $\neg \mathrm T$ , but not both. A true proposition $\mathrm T$ is called a theorem. We will always make the following notations:

$\mathrm T =\mathrm T,\quad \neg \mathrm T = \neg \mathrm T,\quad \mathrm T \neq \neg \mathrm T,\quad \neg \mathrm T\neq \mathrm T.$

This is technically known as the law of excluded middle, which agrees with our intuition of truth. We will use this starting point for further discussion.

It helps us at times to make the abbreviation $\mathrm F := \neg \mathrm T$ , called false. These are called truth values. This gives us the following definition for the negation.

Definition 2. The negation $\neg$ is defined as follows:

$\neg \mathrm T = \mathrm F,\quad \neg \mathrm F := \mathrm T.$

To condense our definitions, we can use a truth table:

This gives us the following observation by repeated uses of said notation:

$\neg(\neg \mathrm T) = \mathrm T,\quad \neg(\neg \mathrm F) = \mathrm F$ .

More generally, we can discuss logic from an algebraic lens.

Definition 3. A propositional variable $p$ is a placeholder that takes on exactly one of the truth values $\mathrm T$ or $\mathrm F$ .

We want to discuss the truth values of two propositional variables $p, q$ . To do that, we need to define the biconditional.

Definition 4. Define the biconditional $\leftrightarrow$ using the following truth table:

For any propositional variable $p$ and any proposition variable $q$ defined in terms of $p$ , we write $p = q$ if $(p \leftrightarrow q)$ is a theorem for any substitution of $p$ .

Theorem 1. Let $p$ be a propositional variable. Then $\neg(\neg p) = p$ .

Proof. We use the following truth table argument:

Many a time, we want to treat theorems as propositional variables. Propositions formed using existing propositions are known as compound statements. We can formalise this using tautologies, with their negations being contradictions.

Definition 5. A compound statement $t$ is a tautology if $t$ is a theorem regardless of substitution of truth values.

With this vocabulary, for any compound statement $p$ and any compound statement $q$ defined in terms of $p$ , we write $p = q$ to mean that $(p \leftrightarrow q) = t$ .

A corollary is a theorem that, for readability purposes, is a straightforward consequence of a previously established theorem.

Corollary 1. For any propositional variable $p$ , $(\neg(\neg p) \leftrightarrow p) = t$ .

A compound statement $c$ is a contradiction if $c = \neg t$ for some tautology $t$ .

Corollary 2. Let $t$ be a tautology and $c$ be a contradiction. Then $c$ is always false, and $\neg c = t$ .

Based on the starting points $\mathrm T$ and $\mathrm F = \neg \mathrm T$ , we can define many logical connectors. One crucial one is known as the conjunction.

Definition 6. Define the conjunction $\wedge$ using the following truth table:

The conjunction has many useful properties. But first, we need to establish some results pertaining tautologies and contradictions. These will be lemmas—theorems that, for readability sake, are intermediate steps to prove more significant theorems.

Lemma 1. Let $p$ be any propositional variable. Then

$p \wedge t = p = t \wedge p, \quad p \wedge c = c = c \wedge p.$

Proof. Use a truth table argument.

We want to eventually prove propositions such as $p \wedge q = q \wedge p$ . However, we first need to prove that we can chain equalities, i.e. that $p=q$ and $q=r$ implies $p=r$ .

Definition 7. Define the implication $\to$ using the following truth table:

To prove our famous results, we need lemmas, which are theorems that, for readability purposes again, are intermediate steps required to prove a theorem.

Lemma 2. For any propositional variable $p$ ,

$(t \to p) = p,\quad (p \to p) = t,\quad (c \to p) = t.$

Proof. Use a truth table argument.

Our next lemma requires us to chain equalities of propositional variables. This helps us prove the commutativity of conjunction.

Lemma 3. For propositional variables $p, q, r$ ,

$(((p=q) \wedge (q=r)) \to (p=r)) = t.$

Proof. We remark that for any substitution of truth values into $p,q,r$ , if $((p=q) \wedge (q=r)) = \mathrm F$ , then

$(((p=q) \wedge (q=r)) \to (p=r)) = \mathrm T$

automatically. Thus, we will suppose that $((p=q) \wedge (q=r)) = \mathrm T$ . By definition of the truth value of the conjunction, we have $p = q$ and $q = r$ .
- Substituting $p$ with $\mathrm T$ , $q=\mathrm T$ and $r = \mathrm T = p$ .
- Substituting $p$ with $\mathrm F$ , $q=\mathrm F$ and $r = \mathrm F = p$ .
Therefore, $p = r$ , as required.

Finally, we can prove the commutativity and associativity property of conjunction.

Theorem 2. Let $p, q, r$ be propositional variables. Then the following hold.

$\begin{aligned} p \wedge q = q \wedge p, \quad (p \wedge q) \wedge r = p \wedge (q \wedge r). \end{aligned}$

Proof. For the first result, use a truth table argument. For the second result, when we substitute $p$ with $\mathrm T$ , we have $p = t$ with respect to $q$ , so that by chaining equalities,

$(p \wedge q) \wedge r = (t \wedge q) \wedge r = q \wedge r = t \wedge (q \wedge r) = p \wedge (q \wedge r) .$

We get the same result when substituting $p$ with $\mathrm F$ .

There is more to say about propositional logic, such as disjunctions and even argument forms, but this post is getting as long as it needs to. Crucially, we have implemented the core elements of propositional logic which we can take advantage of in future topics.

—Joel Kindiak, 15 Nov 24, 2359H
January 9, 2025

logic, math, mathematics, Probability, research
What Makes Strong Induction Strong?
In introductory discrete mathematics, we are introduced to a powerful proof technique called the principle of mathematical induction, which is commonly formulated as follows.

Mathematical Induction. Let $\phi$ be a predicate on $\mathbb N$ . Suppose $\phi(0)$ and for any $k \in \mathbb N$ , $\phi(k) \Rightarrow \phi(k+1)$ . Then for any $n \in \mathbb N$ , $\phi(n)$ .

Proof of Mathematical Induction. Let $K := \{n \in \mathbb N : \phi(n)\} \subseteq \mathbb N$ . By the first condition, $0 \in K$ . By the second condition, we obtain the equivalent formulation $k \in K \Rightarrow k+1 \in K$ . By a core property of $\mathbb N$ , $K = \mathbb N$ .

The condition $\phi(0)$ is known as the base case and the condition “for any $k \in \mathbb N$ , $\phi(k) \Rightarrow \phi(k+1)$ ” is known as the induction step. Students are introduced to a stronger variant of induction known as strong induction.

Strong Induction. Let $\phi$ be a predicate on $\mathbb N$ . Suppose $\phi(0)$ and for any $k \in \mathbb N$ , $\phi(0),\phi(1),\dots,\phi(k) \Rightarrow \phi(k+1)$ . Then for any $n \in \mathbb N$ , $\phi(n)$ .

The difference here is that we have more tools to work with. We will use strong induction to prove the existence part of the fundamental theorem of arithmetic.

Proof of Strong Induction. Suppose $\phi(0)$ and for any $k \in \mathbb N$ , $\phi(0),\phi(1),\dots,\phi(k) \Rightarrow \phi(k+1)$ . Let $\Phi$ be the predicate defined on $\mathbb N$ by

$\Phi(n) = (\forall k\in \mathbb N\quad (k \leq n \ \Rightarrow \ \phi(k))).$

We will use standard induction to prove that for any $n\in \mathbb N$ , $\Phi(n)$ . Since $n \leq n$ , this implies $\phi(n)$ , as required.

For the base case, fix $k \in \mathbb N$ such that $k \leq 0$ . Then $k = 0$ , and by the first condition, $\phi(k) = \phi(0)$ holds. Therefore, $\Phi(0)$ .

For the induction step, fix $k \in \mathbb N$ and suppose $\Phi(k)$ . By definition, for any $m \in \mathbb N$ , $m \leq k$ implies $\phi(m)$ . Therefore, $\phi(0),\phi(1),\dots,\phi(k)$ . By the second condition, $\phi(k+1)$ . Therefore, for any $m \in \mathbb N$ , $m \leq k+1$ implies $\phi(m)$ . This is equivalent to $\Phi(k+1)$ . Therefore, $\Phi(k+1)$ , as required.

Therefore, $\Phi(0)$ and for any $k \in \mathbb N$ , $\Phi(k)$ implies $\Phi(k+1)$ . By induction, for any $n \in \mathbb N$ , $\Phi(n)$ , as required.

As promised, we prove that every natural number can be factored into a unique product of primes.

Fundamental Theorem of Arithmetic. For any number $n \in \mathbb N$ such that $n \geq 2$ , there exist primes $p_1,\dots,p_N$ such that

$\displaystyle n = p_1 \cdots p_N = \prod_{k=1}^N p_k.$

Furthermore, the factorisation is unique in the following sense: if $p_1 \leq \dots \leq p_N$ and $q_1 \leq \dots \leq q_M$ are primes such that

$\displaystyle n = \prod_{i=1}^N p_i = \prod_{j=1}^M q_j,$

then $M=N$ and for any $1 \leq i \leq N$ , $p_i = q_i$ .

Proof of the Fundamental Theorem of Arithmetic. We will use strong induction to establish existence. Let $\phi$ be a predicate on $\mathbb N$ defined by $\phi(n)$ precisely when $n + 2$ can be factored into primes. Clearly, $0 +2 = 2$ is factored into the prime $2$ , so that $\phi(0)$ . Suppose for any $k \in \mathbb N$ , $\phi(0),\phi(1),\dots,\phi(k)$ . We need to establish $\phi(k+1)$ .

Consider the number $k+1 +2 = k +3$ . There are two cases. Either $k+3$ is prime, or not. If $k+3$ is prime, then it is factored into $k+3$ , as required. If $k+3$ is not prime, then $k+3$ is composite. This means that there exist positive integers $r, s \geq 2$ such that $k+3 = rs >\max\{r, s\}$ . Since $2 \leq r, s < k+1+2$ , by the induction hypothesis, there exist primes $p_i$ and $q_j$ such that

$\displaystyle r = \prod_{i = 1}^N p_i,\quad s = \prod_{j = 1}^M q_j.$

Hence, letting $r_l$ denote the primes in non-decreasing sequence,

$\displaystyle k+3 = rs = \prod_{i = 1}^N p_i \cdot \prod_{j = 1}^M q_j = \prod_{l = 1}^{M+N} r_l,$

as required. Therefore, for any $n \in \mathbb N$ , $\phi(n)$ . This is equivalent to the original existence proposition.

We will use Euclid’s lemma to establish uniqueness, for the sake of completeness. As an aside, Euclid’s lemma will be proved independently from the fundamental theorem of arithmetic, so that we do not incur a circular-reasoning fallacy.

Suppose $p_1 \leq \dots \leq p_N$ and $q_1 \leq \dots \leq q_M$ are primes such that

$\displaystyle n = \prod_{i=1}^N p_i = \prod_{j=1}^M q_j.$

We claim that $p_1 = q_1$ . Repeating the argument $\min\{N,M\}$ times then yields the result. Fix $i$ . By Euclid’s lemma, there exists $j$ such that $p_i \mid q_j$ . Thus, there exists some integer $k$ such that $q_j = kp_i$ . Since $q_j$ is prime, $q_j \mid k$ or $q_j \mid p_i$ .
- If $q_j \mid k$ , find an integer $l$ such that $k = q_j l$ . Then $q_j = kp_i = q_j l p_i \Rightarrow lp_i = 1 \Rightarrow p_i = 1$ , a contradiction.
- If $q_j \mid p_i$ , then a similar argument yields $p_i = q_j$ .
Next, we show that $p_1 = q_1$ . Otherwise, there exists $j$ such that $q_1 < q_j = p_1$ . By Euclid’s lemma again, there exists $i$ such that $q_1 \mid p_i$ . A similar argument yields $q_1 = p_i \geq p_1 > q_1$ , a contradiction.

To conclude, strong induction affords us not just $\phi(k)$ , from which we need to prove $\phi(k+1)$ , but furthermore the whole sleuth of $\phi(0),\phi(1),\dots,\phi(k)$ , using any of which or even any combination thereof, to prove $\phi(k+1)$ .

Strong induction even helps us reason about the well-ordering principle, and we need that principle to establish long division. We do that next time.

—Joel Kindiak, 13 Nov 24, 0017H
November 13, 2024

machine-learning, math, mathematics, number-theory, Probability

Tag: Probability

Limits

Differentiation

Integration