KindiakMath

Tag: research

The Logic of Logic
If pure mathematics is a language, then numbers and variables constitute letters, definitions constitute words, and theorems constitute short paragraphs, all building up to a unified story that explains the explanation for the world. What is its grammar? Logic.

Definition 1. A proposition is a sentence that is either true, denoted $\mathrm T$ , or not, denoted $\neg \mathrm T$ , but not both. A true proposition $\mathrm T$ is called a theorem. We will always make the following notations:

$\mathrm T =\mathrm T,\quad \neg \mathrm T = \neg \mathrm T,\quad \mathrm T \neq \neg \mathrm T,\quad \neg \mathrm T\neq \mathrm T.$

This is technically known as the law of excluded middle, which agrees with our intuition of truth. We will use this starting point for further discussion.

It helps us at times to make the abbreviation $\mathrm F := \neg \mathrm T$ , called false. These are called truth values. This gives us the following definition for the negation.

Definition 2. The negation $\neg$ is defined as follows:

$\neg \mathrm T = \mathrm F,\quad \neg \mathrm F := \mathrm T.$

To condense our definitions, we can use a truth table:

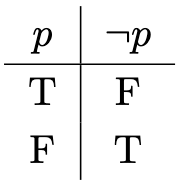
This gives us the following observation by repeated uses of said notation:

$\neg(\neg \mathrm T) = \mathrm T,\quad \neg(\neg \mathrm F) = \mathrm F$ .

More generally, we can discuss logic from an algebraic lens.

Definition 3. A propositional variable $p$ is a placeholder that takes on exactly one of the truth values $\mathrm T$ or $\mathrm F$ .

We want to discuss the truth values of two propositional variables $p, q$ . To do that, we need to define the biconditional.

Definition 4. Define the biconditional $\leftrightarrow$ using the following truth table:

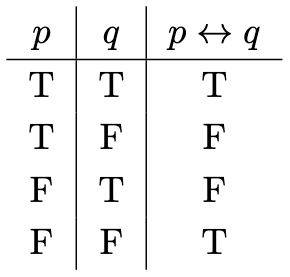
For any propositional variable $p$ and any proposition variable $q$ defined in terms of $p$ , we write $p = q$ if $(p \leftrightarrow q)$ is a theorem for any substitution of $p$ .

Theorem 1. Let $p$ be a propositional variable. Then $\neg(\neg p) = p$ .

Proof. We use the following truth table argument:

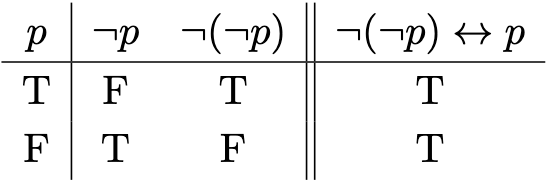
Many a time, we want to treat theorems as propositional variables. Propositions formed using existing propositions are known as compound statements. We can formalise this using tautologies, with their negations being contradictions.

Definition 5. A compound statement $t$ is a tautology if $t$ is a theorem regardless of substitution of truth values.

With this vocabulary, for any compound statement $p$ and any compound statement $q$ defined in terms of $p$ , we write $p = q$ to mean that $(p \leftrightarrow q) = t$ .

A corollary is a theorem that, for readability purposes, is a straightforward consequence of a previously established theorem.

Corollary 1. For any propositional variable $p$ , $(\neg(\neg p) \leftrightarrow p) = t$ .

A compound statement $c$ is a contradiction if $c = \neg t$ for some tautology $t$ .

Corollary 2. Let $t$ be a tautology and $c$ be a contradiction. Then $c$ is always false, and $\neg c = t$ .

Based on the starting points $\mathrm T$ and $\mathrm F = \neg \mathrm T$ , we can define many logical connectors. One crucial one is known as the conjunction.

Definition 6. Define the conjunction $\wedge$ using the following truth table:

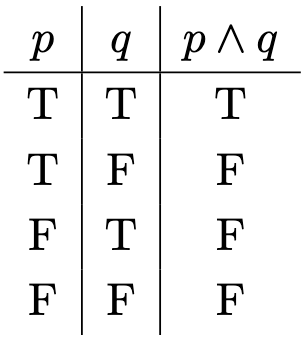
The conjunction has many useful properties. But first, we need to establish some results pertaining tautologies and contradictions. These will be lemmas—theorems that, for readability sake, are intermediate steps to prove more significant theorems.

Lemma 1. Let $p$ be any propositional variable. Then

$p \wedge t = p = t \wedge p, \quad p \wedge c = c = c \wedge p.$

Proof. Use a truth table argument.

We want to eventually prove propositions such as $p \wedge q = q \wedge p$ . However, we first need to prove that we can chain equalities, i.e. that $p=q$ and $q=r$ implies $p=r$ .

Definition 7. Define the implication $\to$ using the following truth table:

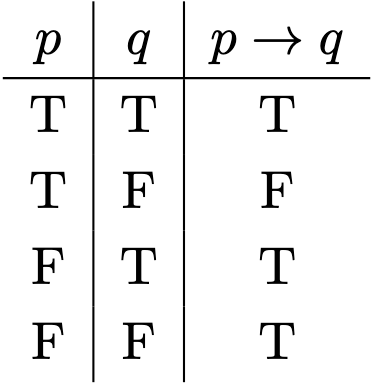
To prove our famous results, we need lemmas, which are theorems that, for readability purposes again, are intermediate steps required to prove a theorem.

Lemma 2. For any propositional variable $p$ ,

$(t \to p) = p,\quad (p \to p) = t,\quad (c \to p) = t.$

Proof. Use a truth table argument.

Our next lemma requires us to chain equalities of propositional variables. This helps us prove the commutativity of conjunction.

Lemma 3. For propositional variables $p, q, r$ ,

$(((p=q) \wedge (q=r)) \to (p=r)) = t.$

Proof. We remark that for any substitution of truth values into $p,q,r$ , if $((p=q) \wedge (q=r)) = \mathrm F$ , then

$(((p=q) \wedge (q=r)) \to (p=r)) = \mathrm T$

automatically. Thus, we will suppose that $((p=q) \wedge (q=r)) = \mathrm T$ . By definition of the truth value of the conjunction, we have $p = q$ and $q = r$ .
- Substituting $p$ with $\mathrm T$ , $q=\mathrm T$ and $r = \mathrm T = p$ .
- Substituting $p$ with $\mathrm F$ , $q=\mathrm F$ and $r = \mathrm F = p$ .
Therefore, $p = r$ , as required.

Finally, we can prove the commutativity and associativity property of conjunction.

Theorem 2. Let $p, q, r$ be propositional variables. Then the following hold.

$\begin{aligned} p \wedge q = q \wedge p, \quad (p \wedge q) \wedge r = p \wedge (q \wedge r). \end{aligned}$

Proof. For the first result, use a truth table argument. For the second result, when we substitute $p$ with $\mathrm T$ , we have $p = t$ with respect to $q$ , so that by chaining equalities,

$(p \wedge q) \wedge r = (t \wedge q) \wedge r = q \wedge r = t \wedge (q \wedge r) = p \wedge (q \wedge r) .$

We get the same result when substituting $p$ with $\mathrm F$ .

There is more to say about propositional logic, such as disjunctions and even argument forms, but this post is getting as long as it needs to. Crucially, we have implemented the core elements of propositional logic which we can take advantage of in future topics.

—Joel Kindiak, 15 Nov 24, 2359H
January 9, 2025

logic, math, mathematics, Probability, research
A Fascinating Multiples Problem
Problem 1. Let $I \subseteq \mathbb Z$ be a subset with the following properties:
- $I \backslash \{0\} \neq \emptyset$ .
- For any $x,y \in I$ , $x+y \in I$ .
- For any $x \in I$ and $\alpha \in \mathbb Z$ , $\alpha x \in I$ .
Prove that there exists $n_0 \in \mathbb Z$ such that $I = \{kn_0 : k \in \mathbb Z\} \equiv n_0 \mathbb Z$ .

(Click for Solution)

Solution. By the first property, there exists some nonzero $n \in I$ . By the third property, $-n = (-1)n \in I$ . Thus, without loss of generality, suppose $n > 0$ .

By the well-ordering principle, there exists some unique $n_0 > 0$ such that

$\displaystyle n_0 = \min \{m \in I : m > 0\}.$

Now we prove that $I = n_0 \mathbb Z$ .

For $(\supseteq)$ , fix $u \in n_0 \mathbb Z$ . Then there exists $k \in \mathbb Z$ such that $u = k n_0 \in I$ .

For $(\subseteq)$ , fix $v \in I$ . By the division algorithm, find integers $q, r$ with $0 \leq r < n_0$ such that $v = qn_0 + r$ .

We claim that $r = 0$ by way of contradiction. Suppose otherwise that $1 \leq r < n_0$ . Then by the third and second properties respectively, $r = v + (-q)n_0 \in I$ .

However, by the definition of $n_0$ , we have $n_0 \leq r < n_0$ , a contradiction.

Therefore, $r = 0$ , which yields $v = qn_0 \in n_0 \mathbb Z$ .

—Joel Kindiak, 31 Oct 24, 0105H
October 31, 2024

machine-learning, math, mathematics, Probability, research
The Exponential Anti-hero

Any Taylor-based calculus joke links to the Taylor series. This is an incredibly powerful technique to approximate non-polynomial functions like $\exp(x) \equiv e^x$ using polynomials.

For this post, we will establish the existence of a Taylor series centred at $0$ , known as a Maclaurin series.

Definition. Define the $n$ -th derivative of $f$ by

$\displaystyle f^{(n)} := \begin{cases} f & \text{if}\, n = 0, \\ (f^{(n-1)})' & \text{if}\, n \geq 1. \end{cases}$

Theorem 1 (Taylor’s Theorem). Suppose $f : (-r, r) \to \mathbb R$ is a real-valued function that is $n$ -times differentiable (that is, $f^{(k)}$ exists for $k=0,1,\dots,n$ on $(-r, r)$ ). Then for any $x \in (0, r)$ , there exists $c \in (0, x)$ such that

$\displaystyle f(x) = f(0) + f'(0)x + \cdots + \frac{f^{(n-1)}(0)}{(n-1)!} x^{n-1} + \frac{f^{(n)}(c)}{n!}x^{n}$ .

More concisely by using summation notation,

$\displaystyle f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k + \frac{f^{(n)}(c)}{n!} x^{n}.$

Before we prove the result, we observe that the case $n=1$ is the vanilla mean value theorem. Furthermore, we actually need to use this special case to prove the general case.

Proof. Fix $x \in (0, r)$ . Define $M$ by

$\displaystyle M := \frac 1{x^n} \left(f(x) - \sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k\right).$

This ensures that

$\displaystyle f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k + M x^{n}.$

Define the $n$ -differentiable function $g : [0, x] \to \mathbb R$ by

$\displaystyle g(t) := f(t) - \left(\sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} t^k + Mt^n\right)$

Direct substitutions yield $g(0) = g'(0) = \cdots = g^{(n-1)}(0)= g(x) = 0$ . Apply the mean value theorem to $g(0) = g(x) = 0$ to find $c_1 \in (0, x)$ such that

$g'(0) = g'(c_1) = 0.$

Apply the mean value theorem $(n-2)$ more times to find $c_{n-1} \in (0, x)$ such that

$g^{(n-1)}(0) = g^{(n-1)}(c_{n-1}) = 0.$

Apply the mean value theorem one last time to find $c_n \in (0, c_{n-1}) \subseteq (0, c_n) \subseteq (0, x)$ such that

$\displaystyle f^{(n)}(c_n) - n! M = g^{(n)}(c_n) = 0 \quad \iff \quad M = \frac{f^{(n)}(c_n)}{n!}.$

Back-substituting yields

$\displaystyle f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k + \frac{f^{(n)}(c)}{n!} x^{n}.$

To use this theorem we need to ensure that $(f^{(n)}(c) / n!) x^{n} \to 0$ as $n \to \infty$ . One way that works is if there exists $M > 0$ such that for any $n$ and for any $t \in (-r, r)$ , $|f^{(n)}(t)| \leq M$ , since

$\displaystyle \left|\frac{f^{(n)}(c)}{n!} x^{n}\right| \leq M \cdot \frac {r^n}{n!} \to 0,$

where $r^n / n! \to 0$ can be established using real-analytic techniques. This criterion works well in the case of the exponential function.

Theorem 2. For any $x \in \mathbb{R}$ ,

$\displaystyle \exp(x) \equiv e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}.$

This is the Maclaurin series of $\exp$ .

Proof. We will suppose $x > 0$ for simplicity. Using $\exp' = \exp$ , for any integer $n \geq 0$ , $f^{(n)}(0) = 1$ and for any $t \in (0, 2x)$ , $|f^{(n)}(t)| \leq e^{2x}$ .

Similarly, we can establish the Maclaurin series for $\sin$ and $\cos$ .

Theorem 3. For any $x \in \mathbb{R}$ ,

$\displaystyle \sin(x) = \sum_{k=0}^{\infty} \frac{{(-1)}^k x^{2k+1}}{(2k+1)!},\quad \cos(x) = \sum_{k=0}^{\infty} \frac{{(-1)}^k x^{k}}{(2k)!}.$

Finally, we can formulate the general Taylor series based on the Maclaurin series.

Theorem 4 (Taylor’s Theorem). Suppose $f : (a-r, a+r) \to \mathbb R$ is a real-valued function that is $n$ -times differentiable. Then for any $x \in (a, a+r)$ , there exists $c \in (a, x)$ such that

$\displaystyle f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x-a)^k + \frac{f^{(n)}(c)}{n!} (x-a)^{n}.$

Proof. Apply the vanilla Taylor’s theorem to the transformed function $g:= f(\cdot + a) : (-r, r) \to \mathbb{R}$ .

—Joel Kindiak, 22 Oct 24, 1517H

October 22, 2024

combinatorics, math, mathematics, physics, research