The Magical Dot Product

Many linear algebra texts open with a definition of the dot product, say in three dimensions, as follows:

$\begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} := u_1 v_1 + u_2 v_2 + u_3 v_3.$

But where on earth did this formula arise from? Other authors open with a geometric definition with the dot product, but I shall open with a simple question: Given two vectors $\mathbf u, \mathbf v \in \mathbb R^2$ in two-dimensional space, what is the angle $\theta$ between $\mathbf u$ and $\mathbf v$ ?

Motivated by the Pythagorean theorem, we can define the length of a two-dimensional vector as follows.

Definition 1. Given $\mathbf v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix}$ , the norm of $\mathbf v$ is defined by

$\|\mathbf v \| := \sqrt{v_1^2 + v_2^2}.$

Intuitively, this quantity captures the length of $\mathbf v$ .

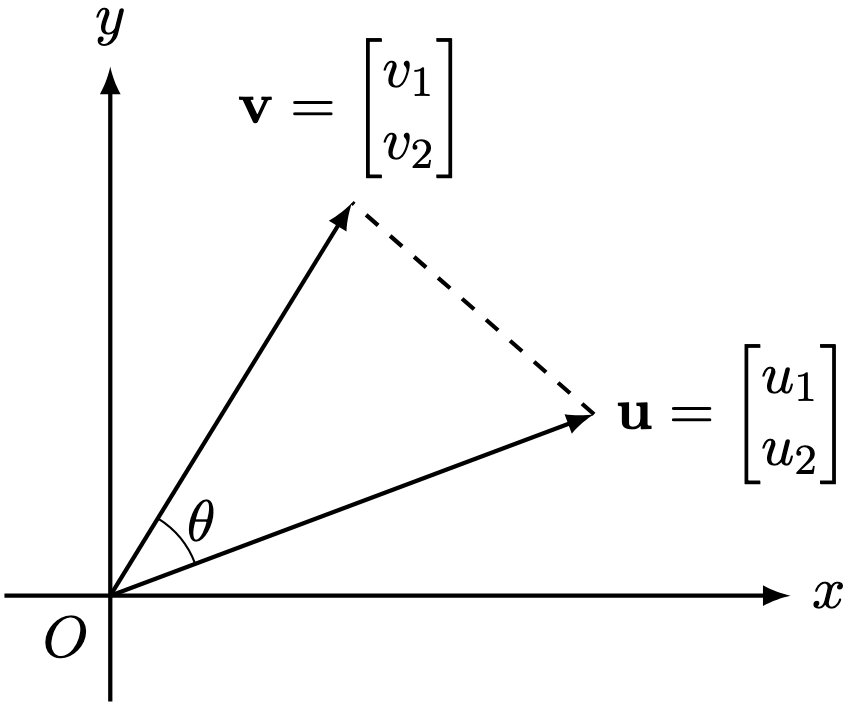
Consider two vectors $\mathbf u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix},\mathbf v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \in \mathbb R^2$ .

Consider the triangle $\Delta OUV$ where $O(0, 0)$ , $U(u_1,u_2)$ , $V(v_1, v_2)$ :

$\begin{aligned} \overrightarrow{VU} &= \overrightarrow{VO} + \overrightarrow{OU} \\ &= \overrightarrow{OU} - \overrightarrow{OV} \\ &= \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} - \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \\ &= \begin{bmatrix} u_1 - v_1 \\ u_2 - v_2 \end{bmatrix}, \end{aligned}$

so that

$\begin{aligned} {VU}^2 &= (u_1 - v_1)^2 + (u_2 - v_2)^2 \\ &= (u_1^2 - 2 u_1 v_1 + v_1^2) + (u_2^2 - 2 u_2 v_2 + v_2^2) \\ &= (u_1^2 + u_2^2) + (v_1^2 + v_2^2) - 2(u_1 v_1 + u_2 v_2)\\ &= OU^2 + OV^2 - 2(u_1 v_1 + u_2 v_2) . \end{aligned}$

Using the law of cosines (or re-deriving its algebraic equivalent),

$\begin{aligned} VU^2 &= OU^2 + OV^2 - 2 \cdot OU \cdot OV \cdot \cos(\theta). \end{aligned}$

Equating the two displays for $VU^2$ then doing algebruh,

$u_1 v_1 + u_2 v_2 = OU \cdot OV \cdot \cos(\theta).$

Therefore, the angle between $\mathbf u, \mathbf v$ can be computed using the sum-product $u_1 v_1 + u_2 v_2$ , which we abbreviate by the dot product notation

$\mathbf u \cdot \mathbf v := u_1 v_1 + u_2 v_2,$

so that we obtain the dot product equation

$\mathbf u \cdot \mathbf v = \| \mathbf u \| \| \mathbf v \| \cos(\theta).$

Yet, the dot product is itself of considerable interest. We can generalise it and talk about angles between other kinds of objects using this idea. This generalisation also features heavily in STEM applications in the form of linear regression. We can even use the dot product to give a theoretically meaningful interpretation to the transpose of a matrix. More on these ideas in future posts.

Theorem 1. For any two vectors $\mathbf u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix},\mathbf v = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \in \mathbb R^2$ in two-dimensional space, define their dot product by

$\mathbf u \cdot \mathbf v := u_1 v_1 + u_2 v_2$ .

The dot product satisfies the following properties:

For any $\mathbf v \in \mathbb R^2$ , $\mathbf v \cdot \mathbf v \geq 0$ .
For any $\mathbf v \in \mathbb R^2$ , $\mathbf v \cdot \mathbf v = 0$ implies $\mathbf v = \mathbf 0$ .
For any $\mathbf u, \mathbf v \in \mathbb R^2$ , $\mathbf u \cdot \mathbf v = \mathbf v \cdot \mathbf u$ .
For any $\mathbf u, \mathbf v \in \mathbb R^2$ , defining $\langle \cdot , \cdot \rangle : \mathbb R^2 \times \mathbb R^2 \to \mathbb R$ by $\langle \mathbf u, \mathbf v \rangle := \mathbf u \cdot \mathbf v$ , the functions $\langle \mathbf u, \cdot \rangle$ and $\langle \cdot, \mathbf v \rangle$ are linear over $\mathbb R$ .

Furthermore, for nonzero $\mathbf u,\mathbf v \in \mathbb R^2$ ,

$\mathbf u \cdot \mathbf v = \| \mathbf u \| \| \mathbf v \| \cos(\theta).$

Proof. The second property is slightly tricky. Fix $\mathbf v \in \mathbb R^2$ . Then

$\mathbf v \cdot \mathbf v = 0 \quad \Rightarrow \quad 0 \leq v_1^2 = v_1^2 + v_2^2 = 0.$

Hence, $v_1 = 0$ . Similarly, $v_2 = 0$ . Therefore, $\mathbf v = \mathbf 0$ .

The dot product motivates the defining properties of the inner product, which we formulate to generalise the dot product.

Let $\mathbb K$ be either $\mathbb R$ or $\mathbb C$ .

Definition 1. A map $\langle \cdot , \cdot \rangle : V \times V \to \mathbb K$ is said to be an inner product on $V$ if it satisfies the following properties:

For any $\mathbf v \in V$ , $\langle \mathbf v, \mathbf v \rangle \in \mathbb R_{\geq 0}$ .
For any $\mathbf v \in V$ , $\langle \mathbf v, \mathbf v \rangle = 0$ implies $\mathbf v = \mathbf 0$ .
For any $\mathbf u, \mathbf v \in V$ , $\langle \mathbf u, \mathbf v \rangle = \overline{\langle \mathbf v, \mathbf u \rangle}$ . When $\mathbb K = \mathbb R$ , we recover usual symmetry.
For any $\mathbf v \in V$ , the map $\langle \cdot ,\mathbf v \rangle : V \to \mathbb K$ is linear.

The pair $V \equiv (V, \langle \cdot, \cdot \rangle)$ is called a $\mathbb K$ –inner product space.

Corollary 1. The dot product of two-dimensional vectors (i.e. in $\mathbb R^2$ ) as defined in Theorem 1 forms an inner product space.

Henceforth, suppose $\langle \cdot, \cdot \rangle$ is an inner product on $V$ .

Lemma 1. For any $\mathbf v \in V$ , define the quadrance of $\mathbf v$ by

$Q(\mathbf v) := \langle \mathbf v, \mathbf v \rangle \in \mathbb R_{\geq 0}.$

The following properties hold:

For any $\mathbf v \in V$ , $Q(\mathbf v) \in \mathbb R_{\geq 0}$ .
For any $\mathbf v \in V$ , $Q(\mathbf v) = 0$ implies $\mathbf v = \mathbf 0$ .
For any $\mathbf v \in V$ , $\alpha \in \mathbb K$ , $Q(\alpha \mathbf v) = |\alpha|^2 Q(\mathbf v)$ .

Proof. For the third property, we have

$\begin{aligned}Q(\alpha \mathbf v) &= \langle \alpha \mathbf v, \alpha \mathbf v \rangle = \alpha \langle \mathbf v, \alpha \mathbf v \rangle \\ &= \alpha \overline{ \langle \alpha \mathbf v, \mathbf v \rangle } = \alpha \overline{ \alpha \langle \mathbf v, \mathbf v \rangle } \\ &= \alpha \overline{\alpha} \overline{ \langle \mathbf v, \mathbf v \rangle } = |\alpha|^2 \langle \mathbf v, \mathbf v \rangle = |\alpha|^2 Q(\mathbf v). \end{aligned}$

Lemma 2 (Cauchy-Schwarz Inequality). For any $\mathbf u, \mathbf v \in V$ ,

$|\langle \mathbf u, \mathbf v \rangle |^2 \leq Q(\mathbf u) Q(\mathbf v).$

Proof. Fix $\mathbf u, \mathbf v \in V$ . If $\langle \mathbf u, \mathbf v \rangle = 0$ , define $\alpha := 1$ . Otherwise, define

$\displaystyle \alpha := \frac{ | \langle \mathbf u,\mathbf v \rangle | }{\langle \mathbf u,\mathbf v \rangle}.$

In either instance, we have $|\alpha| = 1$ and $\alpha \langle \mathbf u,\mathbf v \rangle = | \langle \mathbf u,\mathbf v \rangle |$ .

Define the function $f_{\alpha} : \mathbb R \to \mathbb R_{\geq 0}$ by

$f_{\alpha}(t) := Q( \alpha t \mathbf u + \mathbf v).$

By expanding the definition of $Q$ , we obtain

$\begin{aligned} f_{\alpha}(t) &= \alpha \bar \alpha Q(\mathbf u) t^2 + (\alpha \langle \mathbf u, \mathbf v \rangle + \bar \alpha \langle \mathbf v, \mathbf u \rangle )t + Q(\mathbf v) \\ &= |\alpha|^2 Q(\mathbf u) t^2 + (| \langle \mathbf u,\mathbf v \rangle | + | \langle \mathbf u,\mathbf v \rangle | )t + Q(\mathbf v) \\ &= Q(\mathbf u) t^2 +2 | \langle \mathbf u,\mathbf v \rangle | t + Q(\mathbf v).\end{aligned}$

Since $f_{\alpha}(t) \geq 0$ for any $t \in \mathbb R$ , we must have

$( 2 | \langle \mathbf u,\mathbf v \rangle | )^2 - 4 Q(\mathbf u) Q(\mathbf v) \leq 0,$

yielding $|\langle \mathbf u, \mathbf v \rangle |^2 \leq Q(\mathbf u) Q(\mathbf v)$ .

Theorem 2. For any $\mathbf v \in V$ , define the norm of $\mathbf v$ by $\| \mathbf v\| := \sqrt{ Q( \mathbf v ) }$ . The following properties hold:

For any $\mathbf v \in V$ , $\| \mathbf v \| \geq 0$ .
For any $\mathbf v \in V$ , $\| \mathbf v \| = 0$ implies $\mathbf v = \mathbf 0$ .
For any $\mathbf v \in V$ , $\alpha \in \mathbb K$ , $\|\alpha \mathbf v \| = |\alpha| \| \mathbf v \|$ .
For any $\mathbf u, \mathbf v \in V$ , $\|\mathbf u + \mathbf v \| \leq \| \mathbf u \| + \| \mathbf v \|$ .

We call $V \equiv (V, \| \cdot \| )$ a normed space.

Proof. For the last result, we use the Cauchy-Schwarz inequality to derive that

$\begin{aligned} \|\mathbf u + \mathbf v \|^2 &= Q(\mathbf u + \mathbf v) \\ &= Q( \mathbf u )+ \langle \mathbf u,\mathbf v \rangle + \langle \mathbf v,\mathbf u \rangle + Q( \mathbf v ) \\ &= \| \mathbf u \|^2 + 2\, \text{Re}(\langle \mathbf u,\mathbf v \rangle) + \| \mathbf v \|^2 \\ &\leq \| \mathbf u \|^2 + 2 \| \mathbf u \| \| \mathbf v \| + \| \mathbf v \|^2 \\ &= (\| \mathbf u \| + \| \mathbf v \| )^2, \end{aligned}$

where we defined $\mathrm{Re}(x+iy) := x$ for $x,y \in \mathbb R$ , and observe that for any $z \in \mathbb C$ , $-|z| \leq \mathrm{Re}(z) \leq |z|$ .

Corollary 2. For any nonzero $\mathbf v \in V$ , define the unit vector $\hat{\mathbf v}$ of $\mathbf v$ by

$\displaystyle \hat{\mathbf v} := \frac{ \mathbf v }{ \| \mathbf v \| }.$

Then $\|\hat{\mathbf v}\| = 1$ . In particular, if $\mathbb K = \mathbb R$ , for nonzero $\mathbf u, \mathbf v$ , define the angle between them $\theta \in [0, \pi]$ by

$\theta := \cos^{-1} (\langle \hat{\mathbf u}, \hat{\mathbf v} \rangle).$

Then $\langle \mathbf u, \mathbf v \rangle = \| \mathbf u \| \| \mathbf v \| \cos(\theta)$ .

Proof. For the final result, we note that $\mathbf u = \| \mathbf u \| \hat{\mathbf u}$ . Then

$\langle \mathbf u, \mathbf v \rangle = \langle \| \mathbf u \| \hat{\mathbf u} , \| \mathbf v \| \hat{\mathbf v} \rangle = \| \mathbf u \| \| \mathbf v \| \langle \hat{\mathbf u}, \hat{\mathbf v} \rangle = \| \mathbf u \| \| \mathbf v \| \cos(\theta).$

Corollary 3. Define the metric $d : V \times V \to \mathbb R$ by the map

$d(\mathbf u,\mathbf v) := \|\mathbf u - \mathbf v \|.$

The following properties hold:

For any $\mathbf u,\mathbf v \in V$ , $d(\mathbf u, \mathbf v) \geq 0$ .
For any $\mathbf v \in V$ , $d(\mathbf v, \mathbf v) = 0$ implies $\mathbf v = \mathbf 0$ .
For any $\mathbf u,\mathbf v \in V$ , $d(\mathbf u, \mathbf v) = d(\mathbf v, \mathbf u)$ .
For any $\mathbf u, \mathbf v, \mathbf w \in V$ , $d(\mathbf u,\mathbf v) \leq d(\mathbf u, \mathbf w) + d(\mathbf w, \mathbf v)$ .

We call $V \equiv (V, d )$ a metric space.

Proof. For the last result, use the observation

$\mathbf u - \mathbf v = (\mathbf u - \mathbf w) + (\mathbf w - \mathbf v).$

Therefore, all inner product spaces are normed spaces, and all normed spaces are metric spaces. By some further investigation, every metric space forms a topological space too. If we took a different generalisation from the usual narrative, we would have explored the notion that all normed spaces are topological vector spaces, which in turn are topological spaces.

Each generalisation has their uses in modern mathematics, but for now, let’s focus on inner product spaces. We will first explore the theory of inner product spaces before exploring their ubiquitous applications across mathematics. In particular, let’s broaden the notion of perpendicularity into orthogonality.

—Joel Kindiak, 12 Mar 25, 1407H

Responses

Generalised Diagonalisation – KindiakMath

January 7, 2026 at 9:52 pm

[…] Next time, we pivot to generalising right angles using inner products. In fact, we revisit a somewhat familiar idea—dot products. […]

LikeLike

Generalised Perpendicularity – KindiakMath

March 19, 2026 at 7:20 pm

[…] inner product on a vector space over a field ( or ) gives us the generalised formulation of the dot product on . In particular, if , then two nonzero vectors have angle defined […]

LikeLike

Baby Approximation Theory – KindiakMath

March 19, 2026 at 11:05 pm

[…] more generally, if is an inner product space over , and is a linear transformation, what would be a “best-fit” solution to the […]

LikeLike

Angle-Preserving Transformations – KindiakMath

March 19, 2026 at 11:34 pm

[…] be an inner product space over , where equals or […]

LikeLike

The Spectral Theorems – KindiakMath

March 19, 2026 at 11:37 pm

[…] be a finite-dimensional inner product space over , and be a linear transformation (or if you’d prefer, linear operator on ). Recall that […]

LikeLike

Constructing the Cross Product – KindiakMath

March 19, 2026 at 11:39 pm

[…] our discussion on the dot product began with a simple question: What is the angle between two vectors? Our study on the cross product […]

LikeLike

Defending Rational Trigonometry – KindiakMath

March 19, 2026 at 11:40 pm

[…] be a field. In the case , we can define the usual inner product on […]

LikeLike

Fréchet Derivatives – KindiakMath

March 22, 2026 at 5:44 pm

[…] denotes the usual dot product on […]

LikeLike

The Magical Dot Product

Share this:

Responses

Leave a comment Cancel reply