KindiakMath

What is a negative number?

Let’s say that you started investing . You bought an asset for , and the price changes.

• If the price increases to , then you have gained .
• If, however, the price decreases to , then you have lost .

A positive number, therefore, represents our idea of an increase in a certain amount. A negative number, therefore, represents our idea of a decrease in a certain amount—i.e. a reverse of an increase.

A useful way to visually think of these ideas is by considering the number line below.

Here, we fix the “no-change” point :

• We represent a positive change using a rightward arrow whose length describes the extent of said change.
• Likewise, we represent a negative change, by flipping the rightarrow into a leftward arrow whose length describes the extent of said change. We denote points to the left of with the negative sign prefix .

It is clear that , since , and so we can “take away” a smaller number from a larger number. This idea, however, fails when trying to make sense of .

However, the number line can help us develop some needful ideas.

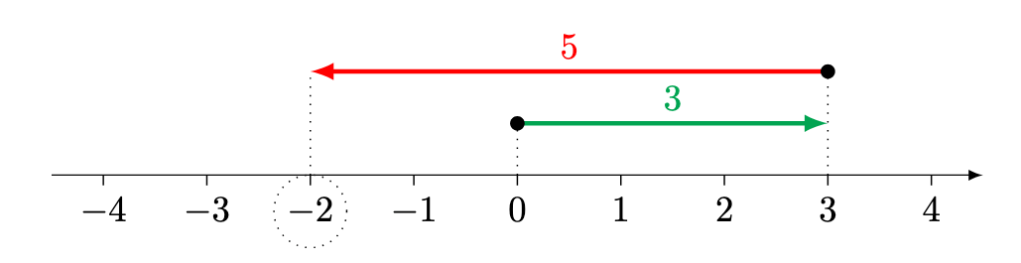
Example 1. Use the number line above to evaluate the expression .

Solution. We re-draw the number line below.

We can read the expression as follows:

• start at , then
• move units rightward , and finally,
• move leftward .

The resulting position is . Therefore,

Since there is nothing special about the numbers and in this example, we obtain the following result:

Lemma 1. Given whole numbers , we can define subtraction by

Proof. Use the number line representation for negative numbers.

Definition 1. A negative number is a number of the form , where is a positive whole number.

• The collection of positive whole numbers, negative numbers, and zero, is together called the collection of integers.

We define addition of integers according to the following rules, where are whole numbers and :

Furthermore, we define subtraction of integers by .

For a more complete construction, see this post that uses higher-level mathematics.

Using the number line above, we see that flipping a unit rightward direction gives the same result as directly moving units leftward :

If we flip a leftward direction , say , then the negative sign flips the leftward direction into a rightward direction :

Definition 2. We define multiplication by to mean

whenever is an integer.

Example 2. Evaluate .

Solution. By Definition 2, and our prior discussion,

Consolidating, we have the following sign conventions.

Lemma 2. The following multiplication of negative signs hold:

Example 3. Evaluate the expressions , , and .

Solution. Using Definition 2,

Similarly,

Finally, using Example 2,

To shorten our working, we use the double negative rule:

Since there is nothing special about the numbers and , we obtain the following multiplication rules involving negative signs:

Theorem 1. Given integers , the following multiplication rules hold:

Proof. Use Definition 2 and Lemma 2 and adapt the solution in Example 3.

At last, expressions of the form make sense, whether are positive numbers, negative numbers, or even just zero.

What we have done works for positive and negative fractions as well. We call them rational numbers, since fractions are ratios of numbers. Filling in the holes between the rational numbers gives us the real numbers, which we picture using the number line. More on that in the next post!

—Joel Kindiak, 18 Sept 25, 1641H