Basic Business Math

Let’s try to make some money.

You want to earn money by selling fidget spinners, but two questions arise:

How much revenue can you earn by selling the fidget spinners?
How much cost would you incur by obtaining the fidget spinners in the first place?

Your profit is then defined by

$(\text{profit}) = (\text{revenue}) - (\text{cost}).$

Let’s first investigate your potential costs.

Example 1. Suppose you buy fidget spinners at a unit cost of $\$2$ per fidget spinner. Make the following definitions:

$x$ represents the number of fidget spinners you obtain.
$\$ y$ represents the total cost of buying $x$ fidget spinners.

What would be the relationship between $x$ and $y$ ?

Solution. Using basic counting,

$(\text{total cost}) = (\text{unit cost}) \times (\text{number of fidget spinners}).$

Hence, $y = 2 \times x$ . For clarity, we suppress the $\times$ symbol and write $y = 2x$ .

Example 2. In Example 1, if you can spend a maximum of $\$30$ , what is the maximum number of fidget spinners you can buy?

Solution. Since the maximum cost is capped at $\$30$ , the maximum number of fidget spinners is captured by setting $y = 30$ :

$\displaystyle 30 = 2x.$

We need to determine the number that $x$ represents (i.e. the value of $x$ ). Recalling that $\frac 12 \cdot 2 = 1$ and $1 \cdot x = x$ ,

$\begin{aligned} \frac 12 \cdot 30 &= \frac 12 \cdot 2x \\ \frac 12 \cdot 2 \cdot 15 &= \frac 12 \cdot 2 \cdot x \\ 1 \cdot 15 &= 1 \cdot x \\ 15 &= x. \end{aligned}$

Therefore, $x = 15$ is the maximum possible number of fidget spinners.

Remark 1. Suppose you had $\$31$ instead. Then the equation

$2x = 31$

produces the value $x = 15.5$ .

We may be tempted to reject the answer $x = 15.5$ , since $0.5$ of a fidget spinner doesn’t arise in real life.
However, if $x$ refers to the number of fidget spinners measured in groups of $10$ , then the answer $x = 15.5$ corresponds to $15.5 \times 10 = 155$ fidget spinners—a perfectly reasonable solution!

Therefore, in general, we can accept non-whole number values of $x$ .

Example 3. If you need to pay a fixed delivery fee of $\$1$ for your fidget spinners, what would your total cost, in terms of $x$ , now be?

Solution. By including the delivery fee,

$\displaystyle y = 2x + 1.$

For example, if $x = 8$ , then $y = 2 \cdot 8 + 1 = 17$ . Here, we write

$a \cdot b + c \equiv (a \cdot b) + c$

using the usual order of operations.

We can picture this relationship using a graph.

The horizontal right arrow, called the $x$ -axis, represents the different possible $x$ -values that we can substitute into the expression.
The vertical up arrow, called the $y$ -axis, represents the different possible $y$ -values that we can obtain.

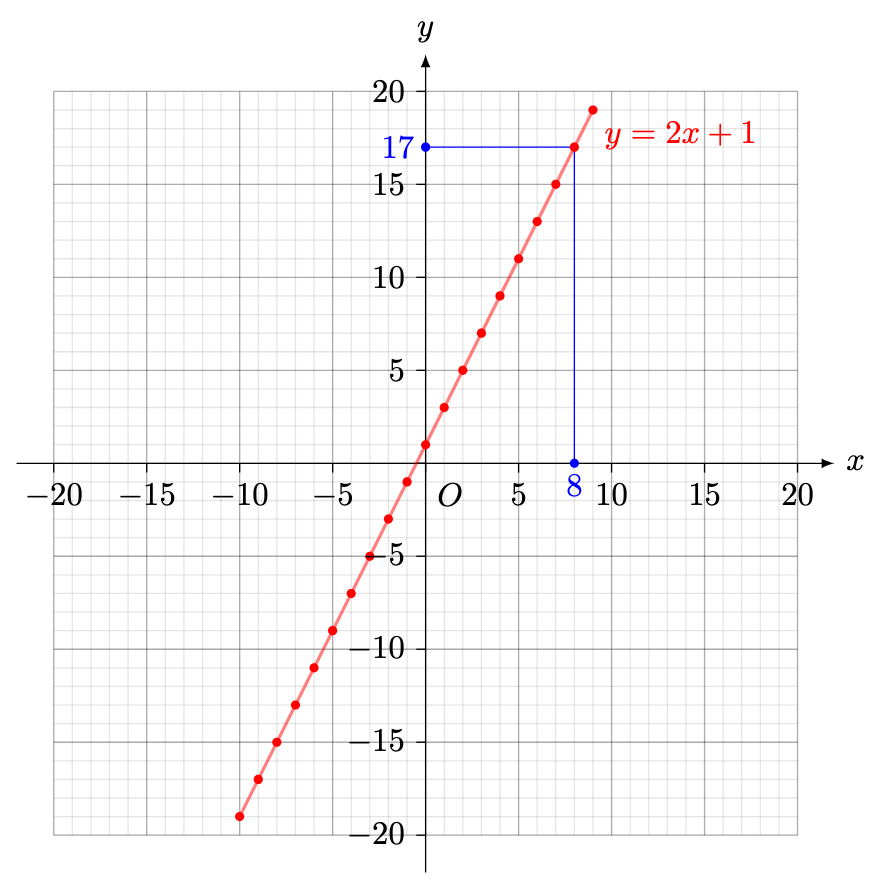
If we allowed $x$ to take non-integer values, we will recover a richer picture. For example, if $x = \frac 12$ , then $y = 2 \cdot \frac 12 + 1 = 2$ . Repeating this process, we get a striking picture:

We recover a straight line!

Example 4. Calculate the change in cost incurred by obtaining one additional fidget spinner. This change is called the gradient of the graph.

Solution. Let $x_0$ be any fixed amount of fidget spinner bought. The cost of buying this number of fidget spinners is

$y_0 = 2x_0 + 1.$

By incrementing the number of fidget spinners, we want to buy $x_1 := x_0 + 1$ fidget spinners and incur a new cost $y_1$ given by

$\begin{aligned} y_1 &= 2x_1 + 1 \\ &= 2(x_0 + 1) + 1 \\ &= 2x_0 + 3. \end{aligned}$

Hence, the required change in cost is

$\begin{aligned} y_1 - y_0 &= (2x_0 + 3) - (2x_0 + 1) \\ &= 2x_0 + 3 - 2x_0 - 1 \\ &= (2x_0 - 2x_0) + (3 - 1) \\ &= 0 + 2 = 2. \end{aligned}$

Example 5. Using $y = 2x + 1$ , calculate the fixed cost that you would incur.

Solution. Setting $x = 0$ , the fixed cost is given by

$y = 2 \cdot 0 + 1 = 1.$

Definition 1. A graph is called a (non-vertical) straight line with:

gradient $m$ ,
$y$ -intercept $c$ ,

if it is continuously drawn using the equation

$y = mx + c.$

The value $m$ describes the steepness of the line:

if $m > 0$ , then the line is upward-sloping,
if $m = 0$ , then the line is horizontal,
if $m < 0$ , then the line is downward-sloping.

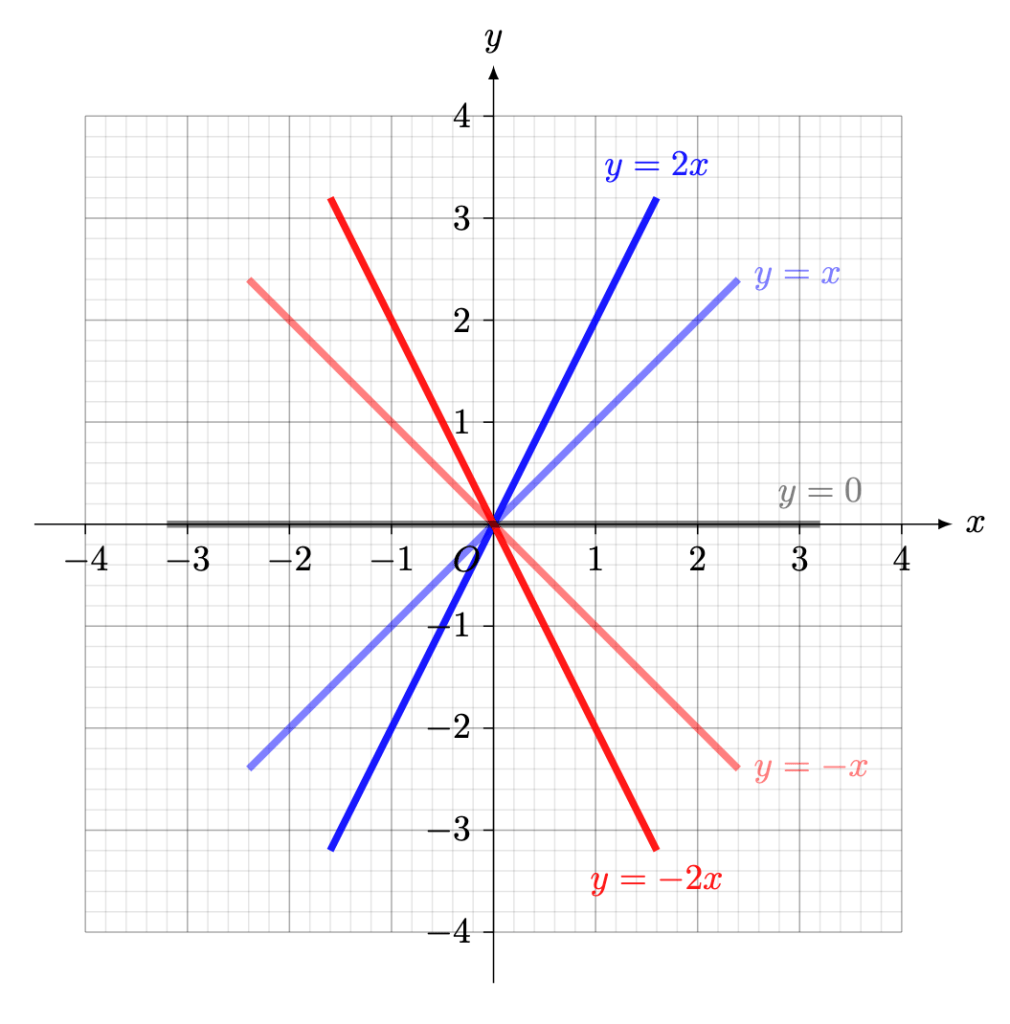
Furthermore,

the more positive the gradient, the steeper the increase,
the more negative the gradient, the steeper the decrease.

The value $c$ fixes the position of the line:

if $c$ is positive, then the $y$ -intercept of the line is positive.
if $c$ is negative, then the $y$ -intercept of the line is negative.
if $c$ is zero, then the line passes .

If $c$ is positive (resp. zero or negative), then the $y$ -intercept of the line is positive (resp. zero or negative).

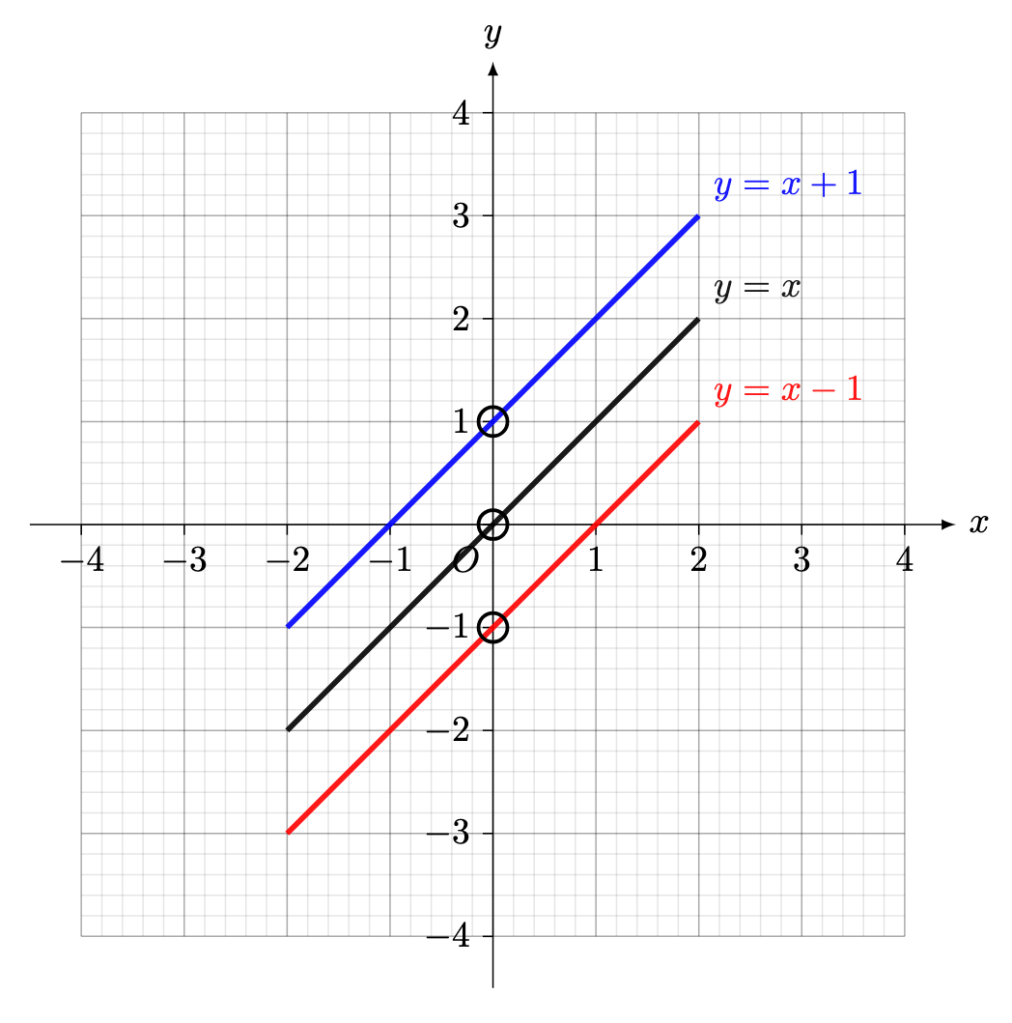
In short,

$m$ describes the steepness of the line,
$c$ fixes the position of the line.

Definition 2. Define a point as a position in space described by a pair of real numbers, denoted $(x_0, y_0)$ , called the coordinates of the point.

Lemma 1. If two points $(x_1,y_1)$ and $(x_2,y_2)$ with $x_1 \neq x_2$ lie on a non-vertical straight line with gradient $m$ , then

$\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}.$

Proof Sketch. Let the non-vertical straight line have equation $y = mx + c$ . Substituting the two pairs of values gives us the equations

$y_1 = mx_1 + c,\quad y_2 = mx_2 + c.$

We leave it as an exercise to check that

$\displaystyle \frac{y_2 - y_1}{x_2 - x_1} = m.$

Lemma 2. The equation of a non-vertical straight line passing through the point $(x_0, y_0)$ with gradient $m$ is given by

$y - y_0 = m(x- x_0).$

Proof Sketch. Using Lemma 1, any point $(x, y)$ that lies on the straight line must satisfy the equation

$\displaystyle \frac{y - y_0}{x - x_0} = m.$

Hence, $y-y_1 = m(x-x_0)$ .

Example 6. You discover that:

$10$ people are willing to pay $\$6$ per fidget spinner,
$16$ people are willing to pay $\$3$ per fidget spinner.

Let $\$ y$ represent the price that $x$ people are willing to buy (of course, one fidget spinner per person).

Stating your assumptions, determine a reasonable relationship between $x$ and $y$ .

Solution. We can picture the two situations in the graph below.

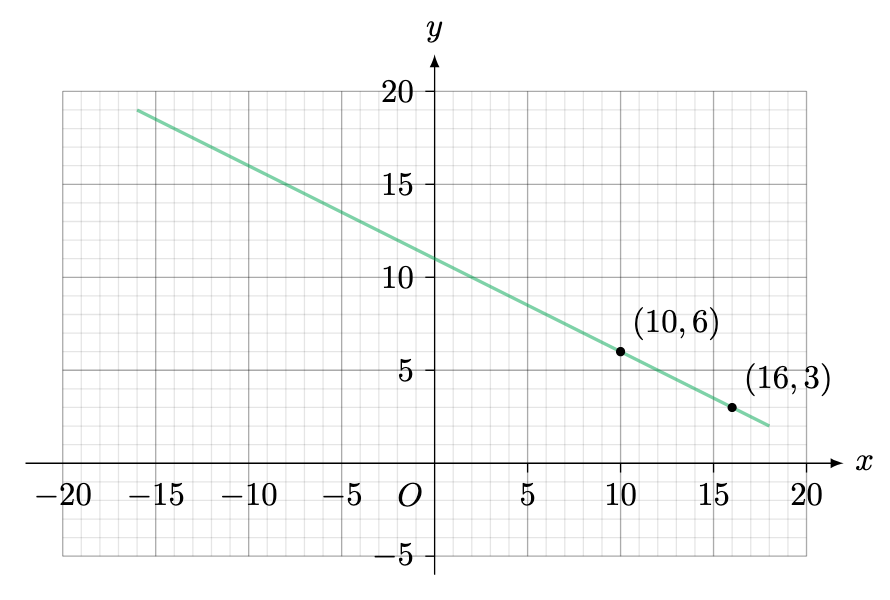
By assuming a straight-line (i.e. linear) graph, we will first apply Lemma 1 using the points $(10, 6)$ and $(16, 3)$ to calculate its gradient:

$\displaystyle m = \frac{3 - 6}{16 - 10} = \frac{-(6-3)}{6} = \frac{-3}{6} = -\frac 12.$

Since the straight line passes through $(10, 6)$ , by Lemma 2, it has the equation

$\begin{aligned} y - 6 &= -\frac 12 \cdot (x-10) \\ &= -\frac 12 \cdot x-\frac 12 \cdot (-10) \\ &= -\frac 12 \cdot x - (-5) \\ &= -\frac 12 \cdot x + 5. \end{aligned}$

Hence, $y = -\frac 12 x + 5 + 6 \Rightarrow y = -\frac 12 x + 11$ .

Definition 3. A graph is a vertical line with $x$ -intercept $c$ if it is continuously drawn using the equation $x = c$ .

Example 7. The line $y = 0$ corresponds to the $x$ -axis and the line $x = 0$ corresponds to the $y$ -axis.

Definition 4. A graph is called a straight line if it can be continuously drawn using the linear equation $ax + by = c$ , where $a, b$ are not both zero.

Theorem 1. A graph is a straight line if and only if it is either a vertical line or a non-vertical straight line.

Proof Sketch. We notice either $b = 0$ or $b \neq 0$ :

Using Definition 3, $b = 0$ holds if and only if the graph is a vertical line.
Using Definition 1, $b \neq 0$ holds if and only if the graph is a non-vertical straight line.

The complete proof using the definitions is left as a good exercise in algebraic manipulation.

Remark 2. This blog post is inspired by ideas in business and economics:

Example 3 pictures the supply curve: how much you are willing to pay in order to sell $x$ fidget spinners.
Example 6 pictures the demand curve: how much people are willing to pay in order to buy $x$ fidget spinners.

Let’s now draw Example 3 and Example 6 on the same graph.

What is the maximum number of fidget spinners that would be worth selling?

Obviously, when the two graphs intersect!

By using our eyeballs (i.e. inspection), the point of intersection has coordinates $(4, 9)$ . However, we will explore this idea more systematically next time without inspection by solving simultaneous equations.

—Joel Kindiak, 27 Sept 25, 1450H

Response

Baby Linear Algebra – KindiakMath

December 17, 2025 at 9:05 pm

[…] Previously, we tried to earn some money selling fidget spinners. The number of fidget spinners that we will sell is given by the intersection point between the two graphs below. […]

LikeLike

Basic Business Math

Share this:

Response

Leave a reply to Baby Linear Algebra – KindiakMath Cancel reply