Algebraic Calculus

Consider the graph of $y = x^2$ below.

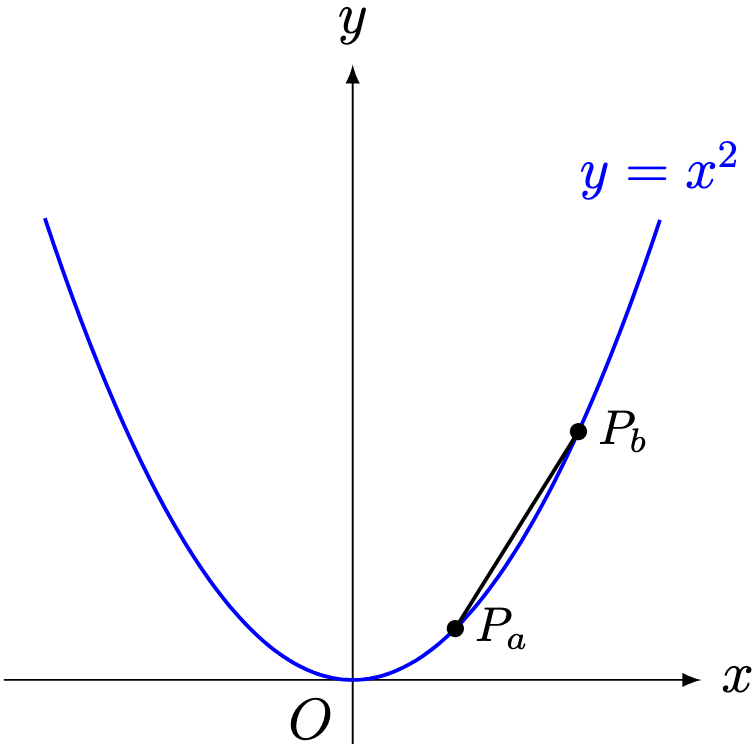
Define the point $P_t$ on the graph by $(t, t^2)$ .

Use this graph to answer Problems 1–4.

Problem 1. Evaluate the gradient of $P_1 P_2$ .

(Click for Solution)

Solution. Since $P_1(1, 1)$ and $P_2(2, 4)$ , the gradient is given by

$\displaystyle m_{P_1P_2} = \frac{4-1}{2-1} = \frac 31 = 3.$

Problem 2. Given $h$ , evaluate the gradient of $P_1 P_{1+h}$ .

Verify your answer in Problem 1.

(Click for Solution)

Solution. Since $P_{1+h}(1+h, (1+h)^2)$ , the gradient is given by

$\begin{aligned} m_{P_1P_{1+h}} &= \frac{(1+h)^2-1}{(1+h)-1} \\ &= \frac{(1+2h+h^2)-1}{(1+h)-1} \\ &= \frac{2h+h^2}{h} \\ &= \frac{(2+h)\cdot h}{h} \\ &= 2+h. \end{aligned}$

This answer agrees with Problem 1, since setting $h = 1$ gives

$\begin{aligned} m_{P_1P_{1+h}} &= 2 + h \\ &= 2 + 1 \\ &= 3 = m_{P_1P_2}. \end{aligned}$

Problem 3. Given $t$ and $h$ , evaluate the gradient of $P_t P_{t+h}$ .

Verify your answer in Problem 2.

(Click for Solution)

Solution. Since $P_t(t,t^2)$ and $P_{t+h}(t+h, (t+h)^2)$ , so that the gradient is given by

$\begin{aligned} m_{P_tP_{t+h}} &= \frac{(t+h)^2-t^2}{(t+h)-t} \\ &= \frac{(t^2+2th+h^2)-t^2}{(t+h)-t} \\ &= \frac{2th+h^2}{h} \\ &= \frac{(2t+h)\cdot h}{h} \\ &= 2t+h. \end{aligned}$

This answer agrees with Problem 2 since setting $t = 1$ gives

$\begin{aligned} m_{P_tP_{t+h}} &= 2t + h \\ &= 2 \cdot 1 + h \\ &= 2 + h \\ &= m_{P_1P_{1+h}}. \end{aligned}$

Problem 4. Let $L_t$ denote the line passing through $P_t$ . Show that $L_t$ is tangent to $y = x^2$ if and only if its gradient is $2t$ .

(Click for Solution)

Solution. Denote the gradient of $L_t$ by $m$ . Then

$L_t : y = m(x - t) + t^2.$

When $L_t$ intersects the curve $y = x^2$ ,

$x^2 = m(x-t) + t^2$

so that solving yields

$\begin{aligned} x^2 - t^2 - m(x-t) &= 0 \\ (x-t)(x+t) - m(x-t) &= 0 \\ (x-t)(x+t-m) &= 0. \end{aligned}$

Then $x = t$ or $x = m - t$ . For $L_t$ to be a tangent to the curve $y = x^2$ at $P_t$ , we must have both roots equal $t$ , so that

$t = m-t \quad \iff \quad m = 2t,$

as required.

Therefore, by setting $h = 0$ in Problem 3, we obtain the answer in Problem 4: the expression $2t$ . Intuitively, this expression describes the gradient of the tangent at $(t, t^2)$ .

Problem 5. Now consider the graph of $y =x^3$ .

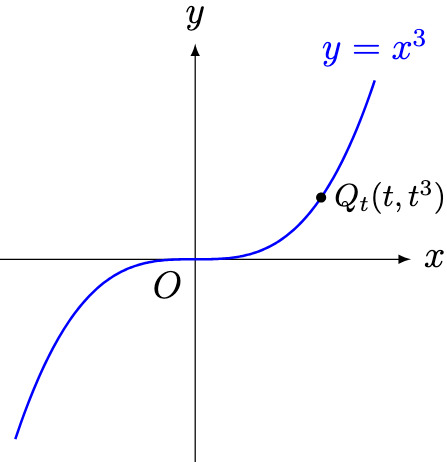
Define the point $Q_t$ on the graph by $(t, t^3)$ .

For any $t$ and $h$ , evaluate the gradient of $Q_t Q_{t+h}$ in terms of $h$ .

(Click for Solution)

Solution. Using the same strategy as per Example 1, since $Q_{t+h}(t+h, (t+h)^3)$ , the gradient is given by

$\begin{aligned} m_{P_tP_{t+h}} &= \frac{(t+h)^3-t^3}{(t+h)-t} = \frac{(t+h)^3-t^3}{ h }. \end{aligned}$

We first expand $(t+h)^3$ :

$\begin{aligned} (t+h)^3 &= (t+h)^2 \cdot (t+h) \\ &= (t^2 + 2th + h^2)(t + h) \\ &= t^3 + (2t^2 + t^2)h + (t+2t)h^2 + h^3 \\ &= t^3 + 3t^2h + 3th^2 + h^3.\end{aligned}$

Therefore,

$\begin{aligned} m_{P_tP_{t+h}} & = \frac{(t+h)^3-t^3}{ h } \\ & = \frac{3t^2h + 3th^2 + h^3}{ h } \\ & = \frac{(3t^2 + 3th + h^2)h}{ h } \\ &= 3t^2 + 3th + h^2. \end{aligned}$

If we set $h = 0$ in the final result, we obtain the expression $3t^2$ . Intuitively, this expression describes the gradient of the tangent at $(t, t^3)$ .