Problem 1. Consider the circle below with equation .
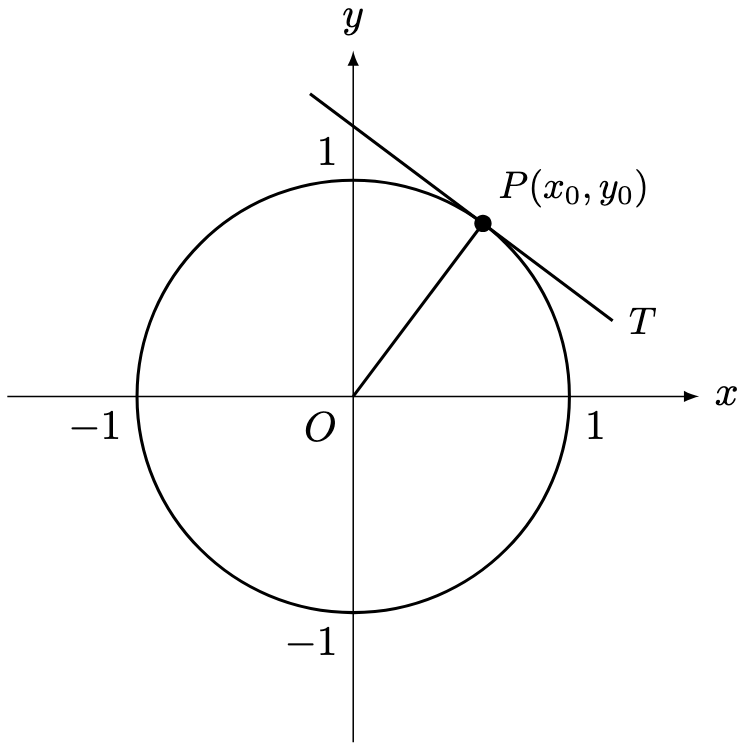
Given and
, calculate the gradient of the tangent
passing through the point
lying on the circle. Deduce that
.
(Click for Solution)
Solution. Since lies on the circle,
For any line with gradient passing through
,
When the line intersects the circle,
Expanding the left-hand side, since ,
Hence, or
For to be a tangent with gradient
, we require
to be the only root. Hence, we must have
Solving for ,
On the other hand, , so that
Therefore, . We recover the tangent is perpendicular to radius property of circles.
Remark 1. The same argument holds for any general circle, with more careful book-keeping.
Problem 2. Given that and
are tangents to the circle, show that
and
bisects
.
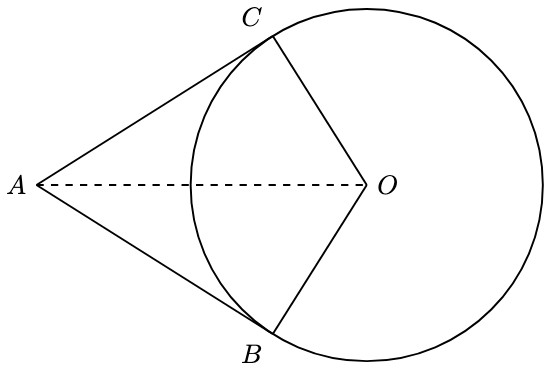
This result is described by the phrase tangent from external point.
(Click for Solution)
Solution. By Problem 1, and
. As radii,
. As a common side,
. Therefore, by the RHS Criterion,
In particular, and
. Hence,
bisects
.
Problem 3. Given that is tangent to the circle, show that
. Deduce that
. This result is known as the alternate segment theorem.
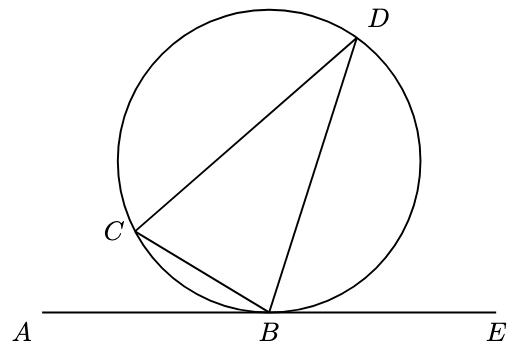
(Click for Solution)
Solution. Make the following constructions, with denoting the centre of the circle.
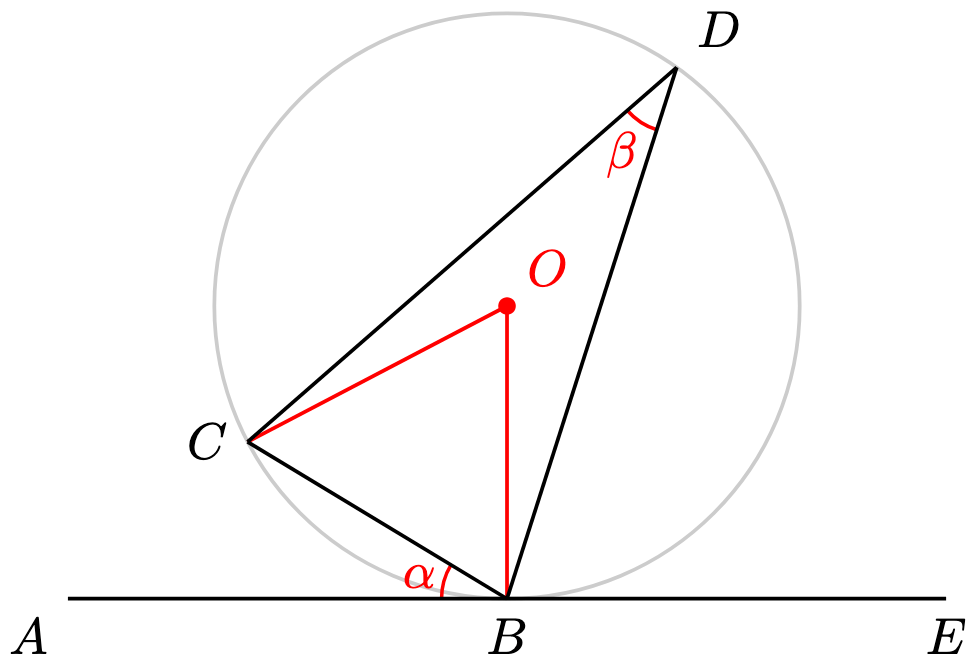
We aim to prove that . By Problem 1,
. Hence,
Since as radii,
is isosceles. Hence,
Since the angle at the centre equals twice the angle at the circumference,
Since angles in a triangle sum to ,
Substituting the displays,
Therefore, , as required.
For the second result,
—Joel Kindiak, 9 Jan 26, 1146H
Leave a comment